|
Vanishing Puzzle
A vanishing puzzle is a mechanical puzzle, mechanical optical illusion comprising multiple pieces which can be rearranged to show different versions of a picture depicting several objects, the number of which depending on the arrangement of the pieces. History Wemple & Company marketed an advertising card named ''The Magic Egg Puzzle, (How Many Eggs?)'' in New York in 1880. Cutting the rectangular card into four oblongs allowed the pieces to be rearranged to show either 8, 9 or 10 eggs. Many other similar puzzles have been published since. Chess player and recreational mathematician Sam Loyd patented rotary vanishing puzzles in 1896 and published versions named ''Get Off the Earth'', ''Teddy and the Lion'' and ''The Disappearing Bicyclist'' (pictured). Each had a circular card connected to a cardboard backdrop with a pin, letting it freely rotate. In ''The Disappearing Bicyclist'', when the disc is rotated such that the arrow points to A, 13 boys can be counted, but when i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Missing Square Puzzle
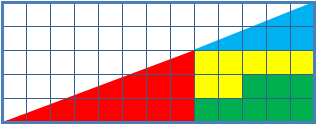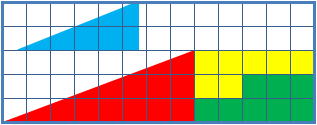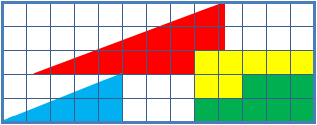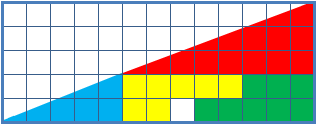
The missing square puzzle is an optical illusion used in mathematics classes to help students reason about geometrical figures; or rather to teach them not to reason using figures, but to use only textual descriptions and the axioms of geometry. It depicts two arrangements made of similar shapes in slightly different configurations. Each apparently forms a 13×5 right-angled triangle, but one has a 1×1 hole in it. Solution The key to the puzzle is the fact that neither of the 13×5 "triangles" is truly a triangle, nor would either truly be 13x5 if it were, because what appears to be the hypotenuse is bent. In other words, the "hypotenuse" does not maintain a consistent slope, even though it may appear that way to the human eye. A true 13×5 triangle cannot be created from the given component parts. The four figures (the yellow, red, blue and green shapes) total 32 units of area. The apparent triangles formed from the figures are 13 units wide and 5 units tall, so it appears ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sam Loyd
Samuel Loyd (January 30, 1841 – April 10, 1911) was an American chess player, chess composer, puzzle author, and recreational mathematics, recreational mathematician. Loyd was born in Philadelphia but raised in New York City. As a chess composer, he authored a number of chess problems, often with interesting themes. At his peak, Loyd was one of the best chess players in the US, and he was ranked 15th in the world, according to chessmetrics.com. He played in the strong Paris 1867 chess tournament (won by Ignatz von Kolisch) with little success, placing near the bottom of the field. Following his death, his book ''Cyclopedia of 5000 Puzzles'' was published (1914) by his son, Samuel Loyd Jr. His son, named after his father, dropped the "Jr" from his name and started publishing reprints of his father's puzzles. Loyd (senior) was inducted into the US Chess Hall of Fame in 1987. Reputation Loyd is widely acknowledged as one of America's great puzzle writers and popularizers, ofte ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Missing Square Puzzle
The missing square puzzle is an optical illusion used in mathematics classes to help students reason about geometrical figures; or rather to teach them not to reason using figures, but to use only textual descriptions and the axioms of geometry. It depicts two arrangements made of similar shapes in slightly different configurations. Each apparently forms a 13×5 right-angled triangle, but one has a 1×1 hole in it. Solution The key to the puzzle is the fact that neither of the 13×5 "triangles" is truly a triangle, nor would either truly be 13x5 if it were, because what appears to be the hypotenuse is bent. In other words, the "hypotenuse" does not maintain a consistent slope, even though it may appear that way to the human eye. A true 13×5 triangle cannot be created from the given component parts. The four figures (the yellow, red, blue and green shapes) total 32 units of area. The apparent triangles formed from the figures are 13 units wide and 5 units tall, so it appears ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
The Disappearing Bicyclist Vanishing Puzzle
''The'' is a grammatical article in English, denoting nouns that are already or about to be mentioned, under discussion, implied or otherwise presumed familiar to listeners, readers, or speakers. It is the definite article in English. ''The'' is the most frequently used word in the English language; studies and analyses of texts have found it to account for seven percent of all printed English-language words. It is derived from gendered articles in Old English which combined in Middle English and now has a single form used with nouns of any gender. The word can be used with both singular and plural nouns, and with a noun that starts with any letter. This is different from many other languages, which have different forms of the definite article for different genders or numbers. Pronunciation In most dialects, "the" is pronounced as (with the voiced dental fricative followed by a schwa) when followed by a consonant sound, and as (homophone of the archaic pronoun ''thee' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Recreational Mathematics
Recreational mathematics is mathematics carried out for recreation (entertainment) rather than as a strictly research-and-application-based professional activity or as a part of a student's formal education. Although it is not necessarily limited to being an endeavor for amateurs, many topics in this field require no knowledge of advanced mathematics. Recreational mathematics involves mathematical puzzles and games, often appealing to children and untrained adults and inspiring their further study of the subject. The Mathematical Association of America (MAA) includes recreational mathematics as one of its seventeen Special Interest Groups, commenting: Mathematical competitions (such as those sponsored by mathematical associations) are also categorized under recreational mathematics. Topics Some of the more well-known topics in recreational mathematics are Rubik's Cubes, magic squares, fractals, logic puzzles and mathematical chess problems, but this area of mathemati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Paradoxes
Mathematics is a field of study that discovers and organizes methods, theories and theorems that are developed and proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of abstract objects that consist of either abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to prove properties of objects, a ''proof'' consisting of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Optical Illusions
In visual perception, an optical illusion (also called a visual illusion) is an illusion caused by the visual system and characterized by a visual percept that arguably appears to differ from reality. Illusions come in a wide variety; their categorization is difficult because the underlying cause is often not clear but a classification proposed by Richard Gregory is useful as an orientation. According to that, there are three main classes: physical, physiological, and cognitive illusions, and in each class there are four kinds: Ambiguities, distortions, paradoxes, and fictions. A classical example for a physical distortion would be the apparent bending of a stick half immersed in water; an example for a physiological paradox is the motion aftereffect (where, despite movement, position remains unchanged). An example for a physiological fiction is an afterimage. Three typical cognitive distortions are the Ponzo, Poggendorff, and Müller-Lyer illusion. Physical illusions are cau ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Missing Dollar Riddle
The missing dollar riddle is a famous riddle that involves an informal fallacy. It dates back to at least the 1930s, although similar puzzles are much older. Statement Although the wording and specifics can vary, the puzzle runs along these lines: Three guests check into a hotel room. The manager says the bill is $30, so each guest pays $10. Later the manager realizes the bill should only have been $25. To rectify this, he gives the bellhop $5 as five one-dollar bills to return to the guests. On the way to the guests' room to refund the money, the bellhop realizes that he cannot equally divide the five one-dollar bills among the three guests. As the guests are not aware of the total of the revised bill, the bellhop decides to just give each guest $1 back and keep $2 as a tip for himself, and proceeds to do so. As each guest got $1 back, each guest only paid $9, bringing the total paid to $27. The bellhop kept $2, which when added to the $27, comes to $29. So if the guests origi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hooper's Paradox
Hooper's paradox is a falsidical paradox based on an optical illusion. A geometric shape with an area of 32 units is dissected into four parts, which afterwards get assembled into a rectangle with an area of only 30 units. Explanation Upon close inspection one can notice that the triangles of the dissected shape are not identical to the triangles in the rectangle. The length of the shorter side at the right angle measures 2 units in the original shape but only 1.8 units in the rectangle. This means, the real triangles of the original shape overlap in the rectangle. The overlapping area is a parallelogram, the diagonals and sides of which can be computed via the Pythagorean theorem. : d_1=\sqrt=\sqrt : d_2=\sqrt=\sqrt : s_1=\sqrt=\sqrt : s_2=\sqrt=\sqrt The area of this parallelogram can determined using Heron's formula for triangles. This yields : s=\frac=\frac for the halved circumference of the triangle (half of the parallelogram) and with that for the area of th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Einstellung Effect
() is the development of a mechanized state of mind. Often called a problem solving set, refers to a person's predisposition to solve a given problem in a specific manner even though better or more appropriate methods of solving the problem exist. The effect is the negative effect of previous experience when solving new problems. The Einstellung effect has been tested experimentally in many different contexts. The example which led to the coining of the term by Abraham S. Luchins and Edith Hirsch Luchins is the Luchins water jar experiment, in which subjects were asked to solve a series of water jar problems. After solving many problems which had the same solution, subjects applied the same solution to later problems even though a simpler solution existed (Luchins, 1942).. Other experiments on the Einstellung effect can be found in ''The Effect of on Compositional Processes'' and ''Rigidity of Behavior, A Variational Approach to the Effect of ''. Background literally mean ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chessboard Paradox
The chessboard paradoxGreg N. Frederickson: ''Dissections: Plane and Fancy''. Cambridge University Press, 2003, , chapter 23, pp. 268–277 in particular pp. 271–274 Colin Foster: "Slippery Slopes". In: ''Mathematics in School'', vol. 34, no. 3 (May, 2005), pp. 33–34JSTOR or paradox of Loyd and SchlömilchFranz Lemmermeyer: ''Mathematik à la Carte: Elementargeometrie an Quadratwurzeln mit einigen geschichtlichen Bemerkungen''. Springer 2014, , pp95–96(German) is a falsidical paradox based on an optical illusion. A chessboard or a square with a side length of 8 units is cut into four pieces. Those four pieces are used to form a rectangle with side lengths of 13 and 5 units. Hence the combined area of all four pieces is 64 area units in the square but 65 area units in the rectangle, this seeming contradiction is due an optical illusion as the four pieces don't fit exactly in the rectangle, but leave a small barely visible gap around the rectangle's diagonal. The paradox is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |