|
Van Lamoen Circle
In Euclidean plane geometry, the van Lamoen circle is a special circle associated with any given triangle T. It contains the circumcenters of the six triangles that are defined inside T by its three medians. Specifically, let A, B, C be the vertices of T, and let G be its centroid (the intersection of its three medians). Let M_a, M_b, and M_c be the midpoints of the sidelines BC, CA, and AB, respectively. It turns out that the circumcenters of the six triangles AGM_c, BGM_c, BGM_a, CGM_a, CGM_b, and AGM_b lie on a common circle, which is the van Lamoen circle of T. History The van Lamoen circle is named after the mathematician who posed it as a problem in 2000. A proof was provided by Kin Y. Li in 2001, and the editors of the Amer. Math. Monthly in 2002. Properties The center of the van Lamoen circle is point X(1153) in Clark Kimberling's comprehensive list of triangle centers. In 2003, Alexey Myakishev and Peter Y. Woo proved that the converse of the theorem is nea ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triangle Center
In geometry, a triangle center or triangle centre is a point in the triangle's plane that is in some sense in the middle of the triangle. For example, the centroid, circumcenter, incenter and orthocenter were familiar to the ancient Greeks, and can be obtained by simple constructions. Each of these classical centers has the property that it is invariant (more precisely equivariant) under similarity transformations. In other words, for any triangle and any similarity transformation (such as a rotation, reflection, dilation, or translation), the center of the transformed triangle is the same point as the transformed center of the original triangle. This invariance is the defining property of a triangle center. It rules out other well-known points such as the Brocard points which are not invariant under reflection and so fail to qualify as triangle centers. For an equilateral triangle, all triangle centers coincide at its centroid. However the triangle centers generally ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parry Circle
In geometry, the Parry point is a special point associated with a plane triangle. It is the triangle center designated ''X''(111) in Clark Kimberling's ''Encyclopedia of Triangle Centers''. The Parry point and Parry circle are named in honour of the English geometer Cyril Parry, who studied them in the early 1990s. Parry circle Let be a plane triangle. The circle through the centroid and the two isodynamic points of is called the Parry circle of . The equation of the Parry circle in barycentric coordinates is 3(b^2-c^2)(c^2-a^2)(a^2-b^2)(a^2yz+b^2zx+c^2xy) + (x+y+z)\left( \sum_\text b^2c^2(b^2-c^2)(b^2+c^2-2a^2)x\right) =0 The center of the Parry circle is also a triangle center. It is the center designated as ''X''(351) in the Encyclopedia of Triangle Centers. The trilinear coordinates of the center of the Parry circle are a(b^2-c^2)(b^2+c^2-2a^2) : b(c^2-a^2)(c^2+a^2-2b^2) : c(a^2-b^2)(a^2+b^2-2c^2) Parry point The Parry circle and the circumcircle of triangle i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
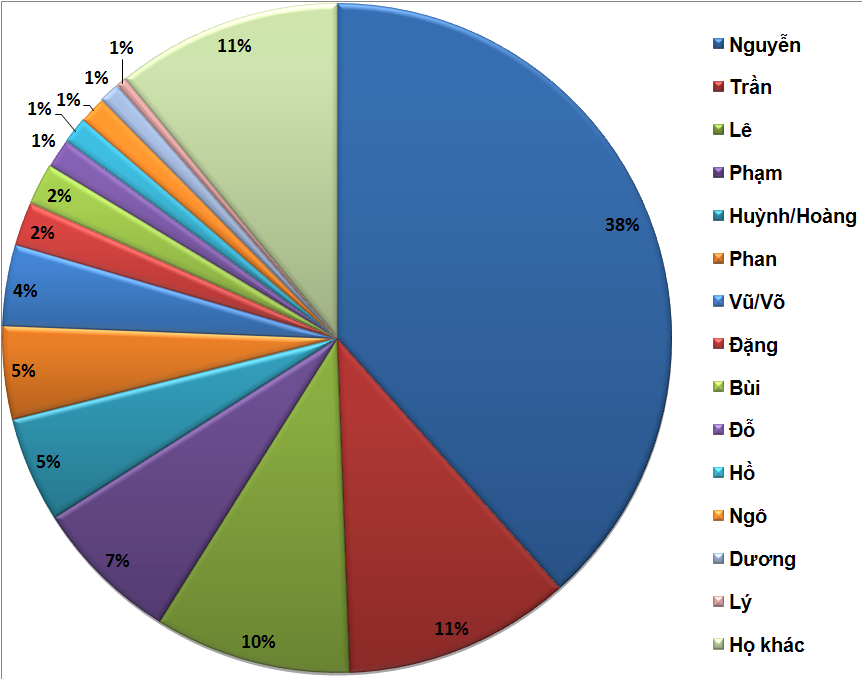
Nguyen Minh Ha
Nguyễn (阮) (sometimes abbreviated as Ng̃) is the most common surname of the Vietnamese people. Outside of Vietnam, the surname is commonly rendered without diacritics as ''Nguyen''. By some estimates 30 to 39 percent of Vietnamese people bear this surname.Lê Trung Hoa, ''Họ và tên người Việt Nam'', NXB Khoa học - Xã hội, 2005 Origin and usage is the transcription of the Sino-Vietnamese pronunciation of the character 阮, which originally was used to write a name of a state in Gansu or ruan, an ancient Chinese instrument. The same Chinese character is often romanized as in Mandarin and as in Cantonese. The first recorded mention of a person surnamed Nguyễn is a description dating AD 317, of a journey to Giao Châu undertaken by Eastern Jin dynasty officer Nguyễn Phu and his family. Many events in Vietnamese history have contributed to the name's prominence. In 1232, after usurping the Lý dynasty, Trần Thủ Độ forced the descendants of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Altitude (triangle)
In geometry, an altitude of a triangle is a line segment through a given Vertex (geometry), vertex (called ''apex (geometry), apex'') and perpendicular to a line (geometry), line containing the side or edge (geometry), edge opposite the apex. This (finite) edge and (infinite) line extension are called, respectively, the ''base (geometry), base'' and ''extended side, extended base'' of the altitude. The point (geometry), point at the intersection of the extended base and the altitude is called the ''foot'' of the altitude. The length of the altitude, often simply called "the altitude" or "height", symbol , is the distance between the foot and the apex. The process of drawing the altitude from a vertex to the foot is known as ''dropping the altitude'' at that vertex. It is a special case of orthogonal projection. Altitudes can be used in the computation of the area of a triangle: one-half of the product of an altitude's length and its base's length (symbol ) equals the triangle's ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orthocenter
The orthocenter of a triangle, usually denoted by , is the point (geometry), point where the three (possibly extended) altitude (triangle), altitudes intersect. The orthocenter lies inside the triangle if and only if the triangle is acute triangle, acute. For a right triangle, the orthocenter coincides with the vertex (geometry), vertex at the right angle. For an equilateral triangle, all triangle center, triangle centers (including the orthocenter) coincide at its centroid. Formulation Let denote the vertices and also the angles of the triangle, and let a = \left, \overline\, b = \left, \overline\, c = \left, \overline\ be the side lengths. The orthocenter has trilinear coordinatesClark Kimberling's Encyclopedia of Triangle Centers \begin & \sec A:\sec B:\sec C \\ &= \cos A-\sin B \sin C:\cos B-\sin C \sin A:\cos C-\sin A\sin B, \end and Barycentric coordinates (mathematics), barycentric coordinates \begin & (a^2+b^2-c^2)(a^2-b^2+c^2) : (a^2+b^2-c^2)(-a^2+b^2+c^2) : (a^2- ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Line Segment
In geometry, a line segment is a part of a line (mathematics), straight line that is bounded by two distinct endpoints (its extreme points), and contains every Point (geometry), point on the line that is between its endpoints. It is a special case of an ''arc (geometry), arc'', with zero curvature. The length of a line segment is given by the Euclidean distance between its endpoints. A closed line segment includes both endpoints, while an open line segment excludes both endpoints; a half-open line segment includes exactly one of the endpoints. In geometry, a line segment is often denoted using an overline (vinculum (symbol), vinculum) above the symbols for the two endpoints, such as in . Examples of line segments include the sides of a triangle or square. More generally, when both of the segment's end points are vertices of a polygon or polyhedron, the line segment is either an edge (geometry), edge (of that polygon or polyhedron) if they are adjacent vertices, or a diagonal. Wh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cevian
In geometry, a cevian is a line segment which joins a vertex of a triangle to a point on the opposite side of the triangle. Medians and angle bisectors are special cases of cevians. The name ''cevian'' comes from the Italian mathematician Giovanni Ceva, who proved a theorem about cevians which also bears his name. Length Stewart's theorem The length of a cevian can be determined by Stewart's theorem: in the diagram, the cevian length is given by the formula :\,b^2m + c^2n = a(d^2 + mn). Less commonly, this is also represented (with some rearrangement) by the following mnemonic: :\underset = \!\!\!\!\!\! \underset Median If the cevian happens to be a median (thus bisecting a side), its length can be determined from the formula :\,m(b^2 + c^2) = a(d^2 + m^2) or :\,2(b^2 + c^2) = 4d^2 + a^2 since :\,a = 2m. Hence in this case :d= \frac\sqrt2 . Angle bisector If the cevian happens to be an angle bisector, its length obeys the formulas :\,(b + c)^2 = a^2 \left( \f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Peter Y
Peter may refer to: People * List of people named Peter, a list of people and fictional characters with the given name * Peter (given name) ** Saint Peter (died 60s), apostle of Jesus, leader of the early Christian Church * Peter (surname), a surname (including a list of people with the name) Culture * Peter (actor) (born 1952), stage name Shinnosuke Ikehata, a Japanese dancer and actor * ''Peter'' (1934 film), a film directed by Henry Koster * ''Peter'' (2021 film), a Marathi language film * "Peter" (''Fringe'' episode), an episode of the television series ''Fringe'' * ''Peter'' (novel), a 1908 book by Francis Hopkinson Smith * "Peter" (short story), an 1892 short story by Willa Cather * ''Peter'' (album), a 1972 album by Peter Yarrow * ''Peter'', a 1993 EP by Canadian band Eric's Trip * "Peter", 2024 song by Taylor Swift from '' The Tortured Poets Department: The Anthology'' Animals * Peter (Lord's cat), cat at Lord's Cricket Ground in London * Peter (chief mouser), Chi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Alexey Myakishev
Alexey ( ; ), is a Russian and Bulgarian male given name derived from the Greek ''Aléxios'' (), meaning "Defender", and thus of the same origin as the Latin Alexius. Similar Ukrainian and Belarusian names are romanized as Oleksii (Олексій) and Aliaksiej (Аляксей), respectively. The Russian Orthodox Church uses the Old Church Slavonic version, Alexiy or Aleksiy (Алексiй, or Алексий in modern spelling), for its Saints and hierarchs (most notably, this is the form used for Patriarchs Alexius I and Alexius II). The name became fairly popular in Russia after the baptism of Michael of Russia's son, Alexis of Russia. The common hypocoristic is Alyosha () or simply Lyosha (). These may be further transformed into Alyoshka, Alyoshenka, Lyoshka, Lyoha, Lyoshenka (, respectively), sometimes rendered as Alesha/Aleshenka in English. The form Alyosha may be used as a full first name in Bulgaria (Альоша) and Armenia. In theory, Alexia is the female f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kimberling Center
The Encyclopedia of Triangle Centers (ETC) is an online list of thousands of points or " centers" associated with the geometry of a triangle. This resource is hosted at the University of Evansville. It started from a list of 400 triangle centers published in the 1998 book Triangle Centers and Central Triangles by Professor Clark Kimberling. , the list identifies 68,547 triangle centers and is managed cooperatively by an international team of geometry researchers. The encyclopedia is integrated into Geogebra. Each point in the list is identified by an index number of the form ''X''(''n'') —for example, ''X''(1) is the incenter. The information recorded about each point includes its trilinear and barycentric coordinates and its relation to lines joining other identified points. Links to The Geometer's Sketchpad diagrams are provided for key points. The encyclopedia also includes a glossary of terms and definitions. Each point in the list is assigned a unique name. In cases wh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclidean Plane
In mathematics, a Euclidean plane is a Euclidean space of Two-dimensional space, dimension two, denoted \textbf^2 or \mathbb^2. It is a geometric space in which two real numbers are required to determine the position (geometry), position of each point (mathematics), point. It is an affine space, which includes in particular the concept of parallel lines. It has also measurement, metrical properties induced by a Euclidean distance, distance, which allows to define circles, and angle, angle measurement. A Euclidean plane with a chosen Cartesian coordinate system is called a ''Cartesian plane''. The set \mathbb^2 of the ordered pairs of real numbers (the real coordinate plane), equipped with the dot product, is often called ''the'' Euclidean plane or ''standard Euclidean plane'', since every Euclidean plane is isomorphic to it. History Books I through IV and VI of Euclid's Elements dealt with two-dimensional geometry, developing such notions as similarity of shapes, the Pythagor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |