|
Type Erasure
In programming languages, type erasure is the load-time process by which explicit type annotations are removed from a program, before it is executed at run-time. Operational semantics not requiring programs to be accompanied by types are named ''type-erasure semantics'', in contrast with ''type-passing semantics''. Type-erasure semantics is an abstraction principle, ensuring that the run-time execution of a program doesn't depend on type information. In the context of generic programming, the opposite of type erasure is named reification. Type inference The reverse operation is named type inference. Though type erasure can be an easy way to define typing over implicitly typed languages (an implicitly typed term is well-typed if and only if it is the erasure of a well-typed explicitly typed lambda term), it doesn't provide Rule of inference Rules of inference are ways of deriving conclusions from premises. They are integral parts of formal logic, serving as norms of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Programming Languages
A programming language is a system of notation for writing computer programs. Programming languages are described in terms of their syntax (form) and semantics (meaning), usually defined by a formal language. Languages usually provide features such as a type system, variables, and mechanisms for error handling. An implementation of a programming language is required in order to execute programs, namely an interpreter or a compiler. An interpreter directly executes the source code, while a compiler produces an executable program. Computer architecture has strongly influenced the design of programming languages, with the most common type ( imperative languages—which implement operations in a specified order) developed to perform well on the popular von Neumann architecture. While early programming languages were closely tied to the hardware, over time they have developed more abstraction to hide implementation details for greater simplicity. Thousands of programming langua ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Loader (computing)
In computing, computer systems a loader is the part of an operating system that is responsible for loading computer program, programs and Library (computing), libraries. It is one of the essential stages in the process of starting a program, as it places programs into memory and prepares them for execution. Loading a program involves either memory-mapped file, memory-mapping or copying the contents of the executable, executable file containing the program instructions into memory, and then carrying out other required preparatory tasks to prepare the executable for running. Once loading is complete, the operating system starts the program by passing control to the loaded program code. All operating systems that support program loading have loaders, apart from highly specialized computer systems that only have a fixed set of specialized programs. Embedded systems typically do not have loaders, and instead, the code executes directly from ROM or similar. In order to load the operatin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Type Signature
In computer science, a type signature or type annotation defines the inputs and outputs of a function, subroutine or method. A type signature includes the number, types, and order of the function's arguments. One important use of a type signature is for function overload resolution, where one particular definition of a function to be called is selected among many overloaded forms. Examples C/C++ In C and C++, the type signature is declared by what is commonly known as a function prototype. In C/C++, a function declaration reflects its use; for example, a function pointer with the signature would be called as: char c; double d; int retVal = (*fPtr)(c, d); Erlang In Erlang, type signatures may be optionally declared, as: -spec function_name(type1(), type2(), ...) -> out_type(). For example: -spec is_even(number()) -> boolean(). Haskell A type signature in Haskell generally takes the following form: functionName :: arg1Type -> arg2Type -> ... -> argNType N ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
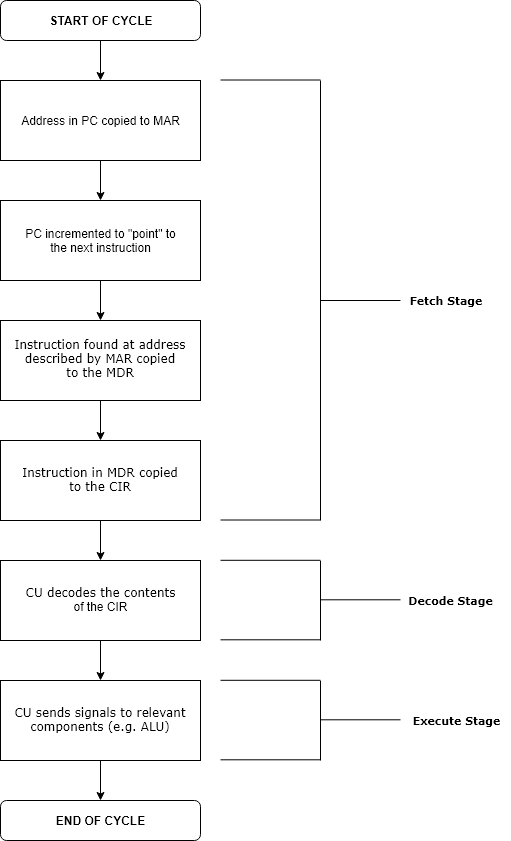
Run Time (program Lifecycle Phase)
Execution in computer and software engineering is the process by which a computer or virtual machine interprets and acts on the instructions of a computer program. Each instruction of a program is a description of a particular action which must be carried out, in order for a specific problem to be solved. Execution involves repeatedly following a " fetch–decode–execute" cycle for each instruction done by the control unit. As the executing machine follows the instructions, specific effects are produced in accordance with the semantics of those instructions. Programs for a computer may be executed in a batch process without human interaction or a user may type commands in an interactive session of an interpreter. In this case, the "commands" are simply program instructions, whose execution is chained together. The term run is used almost synonymously. A related meaning of both "to run" and "to execute" refers to the specific action of a user starting (or ''launching'' o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Operational Semantics
Operational semantics is a category of formal programming language semantics in which certain desired properties of a program, such as correctness, safety or security, are verified by constructing proofs from logical statements about its execution and procedures, rather than by attaching mathematical meanings to its terms (denotational semantics). Operational semantics are classified in two categories: structural operational semantics (or small-step semantics) formally describe how the ''individual steps'' of a computation take place in a computer-based system; by opposition natural semantics (or big-step semantics) describe how the ''overall results'' of the executions are obtained. Other approaches to providing a formal semantics of programming languages include axiomatic semantics and denotational semantics. The operational semantics for a programming language describes how a valid program is interpreted as sequences of computational steps. These sequences then ''are'' the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Abstraction Principle (computer Programming)
In software engineering and programming language theory, the abstraction principle (or the principle of abstraction) is a basic dictum that aims to reduce duplication of information in a program (usually with emphasis on code duplication) whenever practical by making use of abstractions provided by the programming language or software libraries. The principle is sometimes stated as a recommendation to the programmer, but sometimes stated as a requirement of the programming language, assuming it is self-understood why abstractions are desirable to use. The origins of the principle are uncertain; it has been reinvented a number of times, sometimes under a different name, with slight variations. When read as recommendations to the programmer, the abstraction principle can be generalized as the "don't repeat yourself" (DRY) principle, which recommends avoiding the duplication of information in general, and also avoiding the duplication of human effort involved in the software development ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Generic Programming
Generic programming is a style of computer programming in which algorithms are written in terms of data types ''to-be-specified-later'' that are then ''instantiated'' when needed for specific types provided as parameters. This approach, pioneered in the programming language ML in 1973, permits writing common functions or data types that differ only in the set of types on which they operate when used, thus reducing duplicate code. Generic programming was introduced to the mainstream with Ada in 1977. With templates in C++, generic programming became part of the repertoire of professional library design. The techniques were further improved and ''parameterized types'' were introduced in the influential 1994 book '' Design Patterns''. New techniques were introduced by Andrei Alexandrescu in his 2001 book '' Modern C++ Design: Generic Programming and Design Patterns Applied''. Subsequently, D implemented the same ideas. Such software entities are known as ''generics'' in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reification (computer Science)
In computer science, reification is the process by which an abstract idea about a computer program, program is turned into an explicit data model or other object created in a programming language. A computable/addressable object—a ''resource''—is created in a system as a proxy for a non computable/addressable object. By means of reification, something that was previously implicit, unexpressed, and possibly inexpressible is explicitly formulated and made available to conceptual (logical or computational) manipulation. Informally, reification is often referred to as "making something a first-class citizen" within the scope of a particular system. Some aspect of a system can be reified at ''language design time'', which is related to Reflection (computer science), reflection in programming languages. It can be applied as a stepwise refinement at ''system design time''. Reification is one of the most frequently used techniques of conceptual analysis and knowledge representation. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Type Inference
Type inference, sometimes called type reconstruction, refers to the automatic detection of the type of an expression in a formal language. These include programming languages and mathematical type systems, but also natural languages in some branches of computer science and linguistics. Nontechnical explanation In a typed language, a term's type determines the ways it can and cannot be used in that language. For example, consider the English language and terms that could fill in the blank in the phrase "sing _." The term "a song" is of singable type, so it could be placed in the blank to form a meaningful phrase: "sing a song." On the other hand, the term "a friend" does not have the singable type, so "sing a friend" is nonsense. At best it might be metaphor; bending type rules is a feature of poetic language. A term's type can also affect the interpretation of operations involving that term. For instance, "a song" is of composable type, so we interpret it as the thing created ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
If And Only If
In logic and related fields such as mathematics and philosophy, "if and only if" (often shortened as "iff") is paraphrased by the biconditional, a logical connective between statements. The biconditional is true in two cases, where either both statements are true or both are false. The connective is biconditional (a statement of material equivalence), and can be likened to the standard material conditional ("only if", equal to "if ... then") combined with its reverse ("if"); hence the name. The result is that the truth of either one of the connected statements requires the truth of the other (i.e. either both statements are true, or both are false), though it is controversial whether the connective thus defined is properly rendered by the English "if and only if"—with its pre-existing meaning. For example, ''P if and only if Q'' means that ''P'' is true whenever ''Q'' is true, and the only case in which ''P'' is true is if ''Q'' is also true, whereas in the case of ''P if Q ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lambda Term
In mathematical logic, the lambda calculus (also written as ''λ''-calculus) is a formal system for expressing computation based on function abstraction and application using variable binding and substitution. Untyped lambda calculus, the topic of this article, is a universal machine, a model of computation that can be used to simulate any Turing machine (and vice versa). It was introduced by the mathematician Alonzo Church in the 1930s as part of his research into the foundations of mathematics. In 1936, Church found a formulation which was logically consistent, and documented it in 1940. Lambda calculus consists of constructing lambda terms and performing reduction operations on them. A term is defined as any valid lambda calculus expression. In the simplest form of lambda calculus, terms are built using only the following rules: # x: A variable is a character or string representing a parameter. # (\lambda x.M): A lambda abstraction is a function definition, taking as in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rules Of Inference
Rules of inference are ways of deriving conclusions from premises. They are integral parts of formal logic, serving as norms of the logical structure of valid arguments. If an argument with true premises follows a rule of inference then the conclusion cannot be false. ''Modus ponens'', an influential rule of inference, connects two premises of the form "if P then Q" and "P" to the conclusion "Q", as in the argument "If it rains, then the ground is wet. It rains. Therefore, the ground is wet." There are many other rules of inference for different patterns of valid arguments, such as '' modus tollens'', disjunctive syllogism, constructive dilemma, and existential generalization. Rules of inference include rules of implication, which operate only in one direction from premises to conclusions, and rules of replacement, which state that two expressions are equivalent and can be freely swapped. Rules of inference contrast with formal fallaciesinvalid argument forms involving lo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |