 |
Trochoid
In geometry, a trochoid () is a roulette curve formed by a circle rolling along a line. It is the curve traced out by a point fixed to a circle (where the point may be on, inside, or outside the circle) as it rolls along a straight line. If the point is on the circle, the trochoid is called ''common'' (also known as a cycloid); if the point is inside the circle, the trochoid is ''curtate''; and if the point is outside the circle, the trochoid is ''prolate''. The word "trochoid" was coined by Gilles de Roberval, referring to the special case of a cycloid. Basic description As a circle of radius rolls without slipping along a line , the center moves parallel to , and every other point in the rotating plane rigidly attached to the circle traces the curve called the trochoid. Let . Parametric equations of the trochoid for which is the -axis are :\begin & x = a\theta - b \sin \theta \\ & y = a - b \cos \theta \end where is the variable angle through which the circle rolls. C ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
Trochoidal Wave
In fluid dynamics, a trochoidal wave or Gerstner wave is an exact solution of the Euler equations for periodic surface gravity waves. It describes a progressive wave of permanent form on the surface of an incompressible fluid of infinite depth. The free surface of this wave solution is an inverted (upside-down) trochoid – with sharper crests and flat troughs. This wave solution was discovered by Gerstner in 1802, and rediscovered independently by Rankine in 1863. The flow field associated with the trochoidal wave is not irrotational: it has vorticity. The vorticity is of such a specific strength and vertical distribution that the trajectories of the fluid parcels are closed circles. This is in contrast with the usual experimental observation of Stokes drift associated with the wave motion. Also the phase speed is independent of the trochoidal wave's amplitude, unlike other nonlinear wave-theories (like those of the Stokes wave and cnoidal wave) and observations. For the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
 |
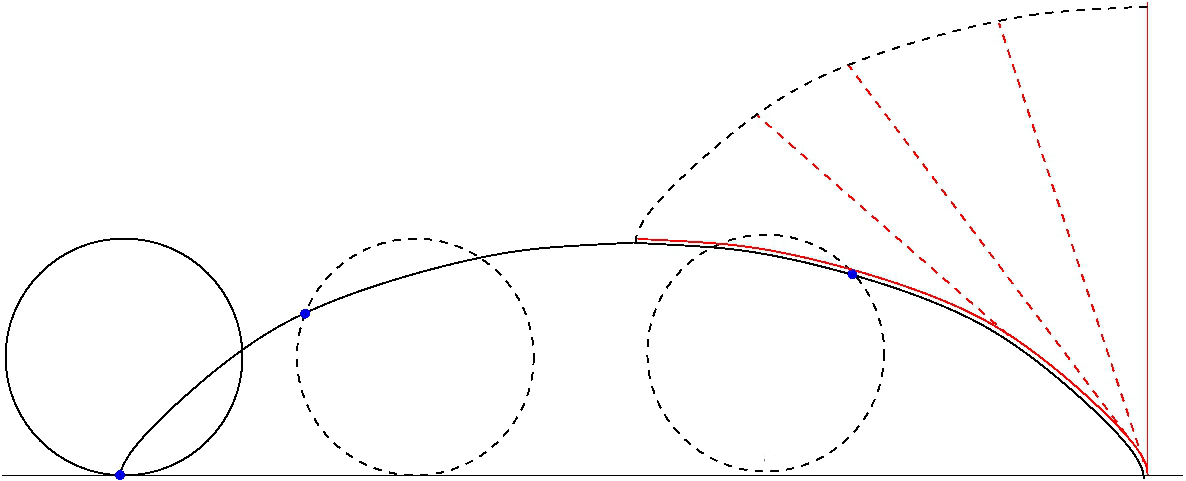
Cycloid
In geometry, a cycloid is the curve traced by a point on a circle as it Rolling, rolls along a Line (geometry), straight line without slipping. A cycloid is a specific form of trochoid and is an example of a roulette (curve), roulette, a curve generated by a curve rolling on another curve. The cycloid, with the Cusp (singularity), cusps pointing upward, is the curve of fastest descent under uniform gravity (the brachistochrone curve). It is also the form of a curve for which the Frequency, period of an object in simple harmonic motion (rolling up and down repetitively) along the curve does not depend on the object's starting position (the tautochrone curve). In physics, when a charged particle at rest is put under a uniform Electric field, electric and magnetic field perpendicular to one another, the particle’s trajectory draws out a cycloid. History The cycloid has been called "The Helen of Geometers" as, like Helen of Troy, it caused frequent quarrels among 17th-centur ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
 |
Cycloid F
In geometry, a cycloid is the curve In mathematics, a curve (also called a curved line in older texts) is an object similar to a line, but that does not have to be straight. Intuitively, a curve may be thought of as the trace left by a moving point. This is the definition that ... traced by a point on a circle as it Rolling, rolls along a Line (geometry), straight line without slipping. A cycloid is a specific form of trochoid and is an example of a roulette (curve), roulette, a curve generated by a curve rolling on another curve. The cycloid, with the Cusp (singularity), cusps pointing upward, is the curve of fastest descent under uniform gravity (the brachistochrone curve). It is also the form of a curve for which the Frequency, period of an object in simple harmonic motion (rolling up and down repetitively) along the curve does not depend on the object's starting position (the tautochrone curve). In physics, when a charged particle at rest is put under a uniform Electr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
Gilles De Roberval
Gilles Personne de Roberval (August 10, 1602 – October 27, 1675) was a French mathematician born at Roberval near Beauvais, France. His name was originally Gilles Personne or Gilles Personier, with Roberval the place of his birth. Biography Like René Descartes, he was present at the Siege of La Rochelle in 1627. In the same year he went to Paris, and in 1631 he was appointed the philosophy chair at Gervais College, Paris. In 1634, he was also made the chair of mathematics at the Royal College of France. A condition of tenure attached to this particular chair was that the holder (Roberval, in this case) would propose mathematical questions for solution, and should resign in favour of any person who solved them better than himself. Notwithstanding this, Roberval was able to keep the chair until his death. Roberval was one of those mathematicians who, just before the invention of the infinitesimal calculus, occupied their attention with problems which are only soluble, or can ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
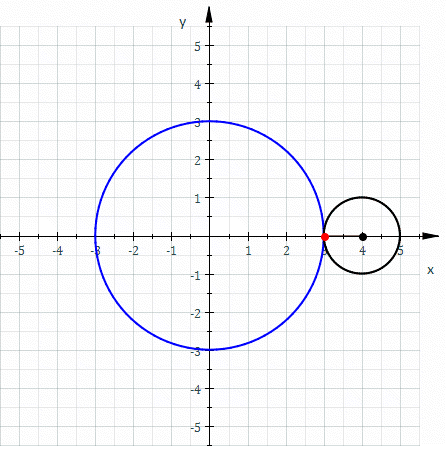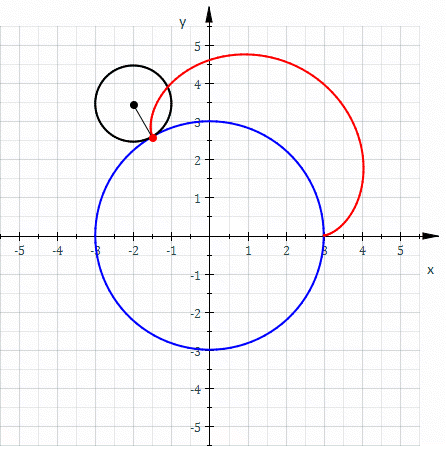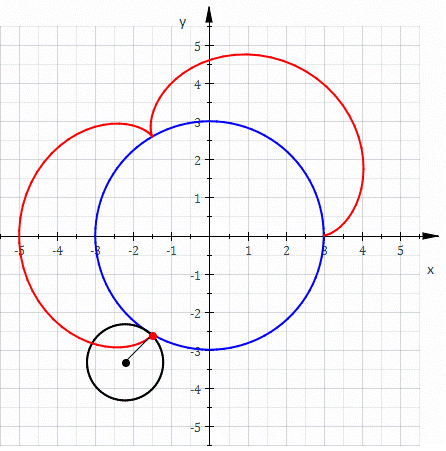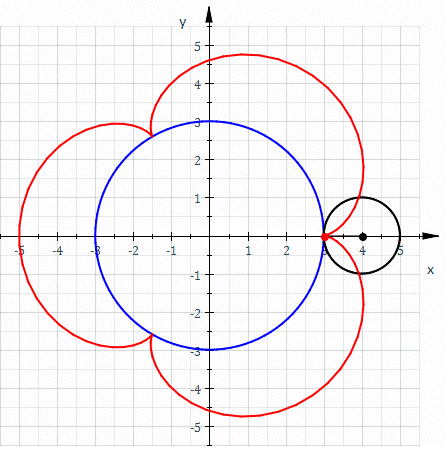 |
Roulette (curve)
In the differential geometry of curves, a roulette is a kind of curve, generalizing cycloids, epicycloids, hypocycloids, trochoids, epitrochoids, hypotrochoids, and involutes. On a basic level, it is the path traced by a curve while rolling on another curve without slipping. Definition Informal definition Roughly speaking, a roulette is the curve described by a point (called the ''generator'' or ''pole'') attached to a given curve as that curve rolls without slipping, along a second given curve that is fixed. More precisely, given a curve attached to a plane which is moving so that the curve rolls, without slipping, along a given curve attached to a fixed plane occupying the same space, then a point attached to the moving plane describes a curve, in the fixed plane called a roulette. Special cases and related concepts In the case where the rolling curve is a line and the generator is a point on the line, the roulette is called an involute of the fixed curve. If the rol ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
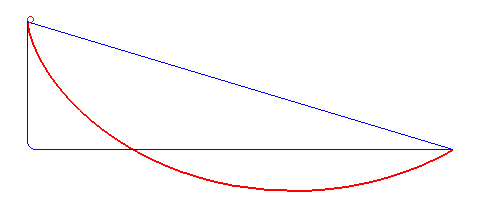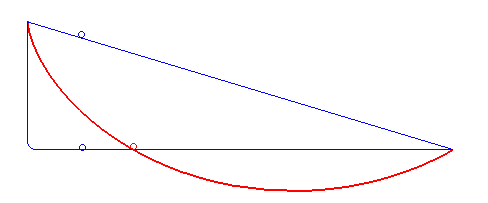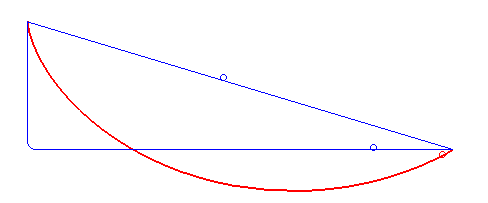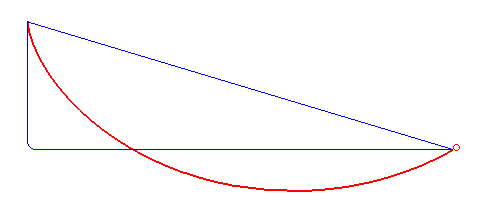 |
Brachistochrone
In physics and mathematics, a brachistochrone curve (), or curve of fastest descent, is the one lying on the plane between a point ''A'' and a lower point ''B'', where ''B'' is not directly below ''A'', on which a bead slides frictionlessly under the influence of a uniform gravitational field to a given end point in the shortest time. The problem was posed by Johann Bernoulli in 1696 and solved by Isaac Newton in 1697. The brachistochrone curve is the same shape as the tautochrone curve; both are cycloids. However, the portion of the cycloid used for each of the two varies. More specifically, the brachistochrone can use up to a complete rotation of the cycloid (at the limit when A and B are at the same level), but always starts at a cusp. In contrast, the tautochrone problem can use only up to the first half rotation, and always ends at the horizontal.Stewart, James. "Section 10.1 - Curves Defined by Parametric Equations." ''Calculus: Early Transcendentals''. 7th ed. Belmont, CA: ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
Aristotle's Wheel Paradox
Aristotle's wheel paradox is a paradox or problem appearing in the Pseudo-Aristotle, pseudo-Aristotelian Ancient Greece, Greek work ''Mechanics (Aristotle), Mechanica''. It states as follows: A wheel is depicted in two-dimensional space as two circles. Its larger, outer circle is tangential to a horizontal surface (e.g. a road that it rolls on), while the smaller, inner one has the same center and is rigidly affixed to the larger. (The smaller circle could be the bead of a tire, the rim it is mounted upon, or the axle.) Assuming the larger circle rolls without slipping (or skidding) for one full revolution, the distances moved by both circles' circumferences are the same. The distance travelled by the larger circle is equal to its circumference, but for the smaller it is greater than its circumference, thereby creating a paradox. The paradox is not limited to wheels: other things depicted in two dimensions display the same behavior such as a roll of tape, or a typical round bottle ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
Line (geometry)
In geometry, a straight line, usually abbreviated line, is an infinitely long object with no width, depth, or curvature, an idealization of such physical objects as a straightedge, a taut string, or a ray (optics), ray of light. Lines are space (mathematics), spaces of dimension one, which may be Embedding, embedded in spaces of dimension two, three, or higher. The word ''line'' may also refer, in everyday life, to a line segment, which is a part of a line delimited by two Point (geometry), points (its ''endpoints''). Euclid's Elements, Euclid's ''Elements'' defines a straight line as a "breadthless length" that "lies evenly with respect to the points on itself", and introduced several postulates as basic unprovable properties on which the rest of geometry was established. ''Euclidean line'' and ''Euclidean geometry'' are terms introduced to avoid confusion with generalizations introduced since the end of the 19th century, such as Non-Euclidean geometry, non-Euclidean, Project ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
Coprime
In number theory, two integers and are coprime, relatively prime or mutually prime if the only positive integer that is a divisor of both of them is 1. Consequently, any prime number that divides does not divide , and vice versa. This is equivalent to their greatest common divisor (GCD) being 1. One says also ''is prime to'' or ''is coprime with'' . The numbers 8 and 9 are coprime, despite the fact that neither—considered individually—is a prime number, since 1 is their only common divisor. On the other hand, 6 and 9 are not coprime, because they are both divisible by 3. The numerator and denominator of a reduced fraction are coprime, by definition. Notation and testing When the integers and are coprime, the standard way of expressing this fact in mathematical notation is to indicate that their greatest common divisor is one, by the formula or . In their 1989 textbook '' Concrete Mathematics'', Ronald Graham, Donald Knuth, and Oren Patashnik proposed an alte ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
Spirograph
Spirograph is a geometric drawing device that produces mathematical roulette curves of the variety technically known as hypotrochoids and epitrochoids. The well-known toy version was developed by British engineer Denys Fisher and first sold in 1965. The name has been a registered trademark of Hasbro Inc. since 1998 following purchase of the company that had acquired the Denys Fisher company. The Spirograph brand was relaunched worldwide in 2013, with its original product configurations, by Kahootz Toys. History In 1827, Greek-born English architect and engineer Peter Hubert Desvignes developed and advertised a "Speiragraph", a device to create elaborate spiral drawings. A man named J. Jopling soon claimed to have previously invented similar methods. When working in Vienna between 1845 and 1848, Desvignes constructed a version of the machine that would help prevent banknote forgeries, as any of the nearly endless variations of roulette patterns that it could produce were ex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
List Of Periodic Functions
This is a list of some well-known periodic functions. The constant function , where is independent of , is periodic with any period, but lacks a ''fundamental period''. A definition is given for some of the following functions, though each function may have many equivalent definitions. Smooth functions All trigonometric functions listed have period 2\pi, unless otherwise stated. For the following trigonometric functions: : is the th up/down number, : is the th Bernoulli number : in Jacobi elliptic functions, q=e^ Non-smooth functions The following functions have period p and take x as their argument. The symbol \lfloor n \rfloor is the floor function of n and \sgn is the sign function. K means Elliptic integral K(m) Vector-valued functions * Epitrochoid * Epicycloid (special case of the epitrochoid) * Limaçon (special case of the epitrochoid) * Hypotrochoid * Hypocycloid (special case of the hypotrochoid) * Spirograph (special case of the hypotrochoid) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |