|
Trial Division
Trial division is the most laborious but easiest to understand of the integer factorization algorithms. The essential idea behind trial division tests to see if an integer , the integer to be factored, can be divided by each number in turn that is less than or equal to the square root of . For example, to find the prime factors of , one can try to divide by successive primes: first, ; next, neither nor evenly divides ; finally, , and is itself prime. So . Trial division was first described by Fibonacci in his book '' Liber Abaci'' (1202). Method Given an integer ''n'' (''n'' refers to "the integer to be factored"), the trial division consists of systematically testing whether ''n'' is divisible by any smaller number. Clearly, it is only worthwhile to test candidate factors less than ''n'', and in order from two upwards because an arbitrary ''n'' is more likely to be divisible by two than by three, and so on. With this ordering, there is no point in testing for divisibili ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Integer Factorization
In mathematics, integer factorization is the decomposition of a positive integer into a product of integers. Every positive integer greater than 1 is either the product of two or more integer factors greater than 1, in which case it is a composite number, or it is not, in which case it is a prime number. For example, is a composite number because , but is a prime number because it cannot be decomposed in this way. If one of the factors is composite, it can in turn be written as a product of smaller factors, for example . Continuing this process until every factor is prime is called prime factorization; the result is always unique up to the order of the factors by the prime factorization theorem. To factorize a small integer using mental or pen-and-paper arithmetic, the simplest method is trial division: checking if the number is divisible by prime numbers , , , and so on, up to the square root of . For larger numbers, especially when using a computer, various more sophis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Quadratic Sieve
The quadratic sieve algorithm (QS) is an integer factorization algorithm and, in practice, the second-fastest method known (after the general number field sieve). It is still the fastest for integers under 100 decimal digits or so, and is considerably simpler than the number field sieve. It is a general-purpose factorization algorithm, meaning that its running time depends solely on the size of the integer to be factored, and not on special structure or properties. It was invented by Carl Pomerance in 1981 as an improvement to Schroeppel's linear sieve. Basic aim The algorithm attempts to set up a congruence of squares modulo ''n'' (the integer to be factorized), which often leads to a factorization of ''n''. The algorithm works in two phases: the ''data collection'' phase, where it collects information that may lead to a congruence of squares; and the ''data processing'' phase, where it puts all the data it has collected into a matrix and solves it to obtain a congruence of squ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Integer Factorization Algorithms
In mathematics, integer factorization is the decomposition of a positive integer into a product of integers. Every positive integer greater than 1 is either the product of two or more integer factors greater than 1, in which case it is a composite number, or it is not, in which case it is a prime number. For example, is a composite number because , but is a prime number because it cannot be decomposed in this way. If one of the factors is composite, it can in turn be written as a product of smaller factors, for example . Continuing this process until every factor is prime is called prime factorization; the result is always unique up to the order of the factors by the prime factorization theorem. To factorize a small integer using mental or pen-and-paper arithmetic, the simplest method is trial division: checking if the number is divisible by prime numbers , , , and so on, up to the square root of . For larger numbers, especially when using a computer, various more sophis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Springer-Verlag
Springer Science+Business Media, commonly known as Springer, is a German multinational publishing company of books, e-books and peer-reviewed journals in science, humanities, technical and medical (STM) publishing. Originally founded in 1842 in Berlin, it expanded internationally in the 1960s, and through mergers in the 1990s and a sale to venture capitalists it fused with Wolters Kluwer and eventually became part of Springer Nature in 2015. Springer has major offices in Berlin, Heidelberg, Dordrecht, and New York City. History Julius Springer founded Springer-Verlag in Berlin in 1842 and his son Ferdinand Springer grew it from a small firm of 4 employees into Germany's then second-largest academic publisher with 65 staff in 1872.Chronology ". Springer Science+Business Media. In 1964, Springer expanded its business internationally, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Undergraduate Texts In Mathematics
Undergraduate Texts in Mathematics (UTM) () is a series of undergraduate-level textbooks in mathematics published by Springer-Verlag. The books in this series, like the other Springer-Verlag mathematics series, are small yellow books of a standard size. The books in this series tend to be written at a more elementary level than the similar Graduate Texts in Mathematics series, although there is a fair amount of overlap between the two series in terms of material covered and difficulty level. There is no Springer-Verlag numbering of the books like in the Graduate Texts in Mathematics series. The books are numbered here by year of publication. List of books # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
RSA-250
In mathematics, the RSA numbers are a set of large semiprimes (numbers with exactly two prime factors) that were part of the RSA Factoring Challenge. The challenge was to find the prime factors of each number. It was created by RSA Laboratories in March 1991 to encourage research into computational number theory and the practical difficulty of factoring large integers. The challenge was ended in 2007. RSA Laboratories (which is an initialism of the creators of the technique; Rivest, Shamir and Adleman) published a number of semiprimes with 100 to 617 decimal digits. Cash prizes of varying size, up to US$200,000 (and prizes up to $20,000 awarded), were offered for factorization of some of them. The smallest RSA number was factored in a few days. Most of the numbers have still not been factored and many of them are expected to remain unfactored for many years to come. , the smallest 23 of the 54 listed numbers have been factored. While the RSA challenge officially ended in 2007, pe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Grid Computing
Grid computing is the use of widely distributed computer resources to reach a common goal. A computing grid can be thought of as a distributed system with non-interactive workloads that involve many files. Grid computing is distinguished from conventional high-performance computing systems such as cluster computing in that grid computers have each node set to perform a different task/application. Grid computers also tend to be more heterogeneous and geographically dispersed (thus not physically coupled) than cluster computers. Although a single grid can be dedicated to a particular application, commonly a grid is used for a variety of purposes. Grids are often constructed with general-purpose grid middleware software libraries. Grid sizes can be quite large. Grids are a form of distributed computing composed of many networked loosely coupled computers acting together to perform large tasks. For certain applications, distributed or grid computing can be seen as a special ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Supercomputer
A supercomputer is a type of computer with a high level of performance as compared to a general-purpose computer. The performance of a supercomputer is commonly measured in floating-point operations per second (FLOPS) instead of million instructions per second (MIPS). Since 2022, supercomputers have existed which can perform over 1018 FLOPS, so called Exascale computing, exascale supercomputers. For comparison, a desktop computer has performance in the range of hundreds of gigaFLOPS (1011) to tens of teraFLOPS (1013). Since November 2017, all of the TOP500, world's fastest 500 supercomputers run on Linux-based operating systems. Additional research is being conducted in the United States, the European Union, Taiwan, Japan, and China to build faster, more powerful and technologically superior exascale supercomputers. Supercomputers play an important role in the field of computational science, and are used for a wide range of computationally intensive tasks in various fields, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Public Key Cryptography
Public-key cryptography, or asymmetric cryptography, is the field of cryptographic systems that use pairs of related keys. Each key pair consists of a public key and a corresponding private key. Key pairs are generated with cryptographic algorithms based on mathematical problems termed one-way functions. Security of public-key cryptography depends on keeping the private key secret; the public key can be openly distributed without compromising security. There are many kinds of public-key cryptosystems, with different security goals, including digital signature, Diffie–Hellman key exchange, public-key key encapsulation, and public-key encryption. Public key algorithms are fundamental security primitives in modern cryptosystems, including applications and protocols that offer assurance of the confidentiality and authenticity of electronic communications and data storage. They underpin numerous Internet standards, such as Transport Layer Security (TLS), SSH, S/MIME, and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
General Number Field Sieve
In number theory, the general number field sieve (GNFS) is the most efficient classical algorithm known for factoring integers larger than . Heuristically, its complexity for factoring an integer (consisting of bits) is of the form : \begin & \exp\left(\left((64/9)^+o(1)\right)\left(\log n\right)^ \left(\log\log n\right)^\right) \\ pt= & L_n\left /3,(64/9)^\right\end in O and L-notations. It is a generalization of the special number field sieve: while the latter can only factor numbers of a certain special form, the general number field sieve can factor any number apart from prime powers (which are trivial to factor by taking roots). The principle of the number field sieve (both special and general) can be understood as an improvement to the simpler rational sieve or quadratic sieve. When using such algorithms to factor a large number , it is necessary to search for smooth numbers (i.e. numbers with small prime factors) of order . The size of these values is exponentia ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
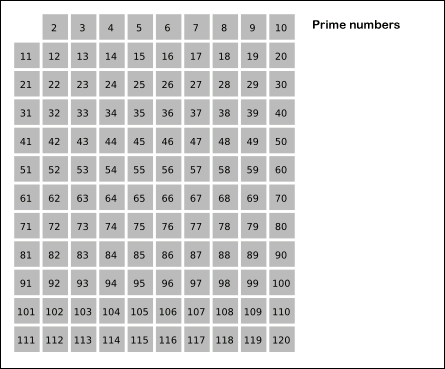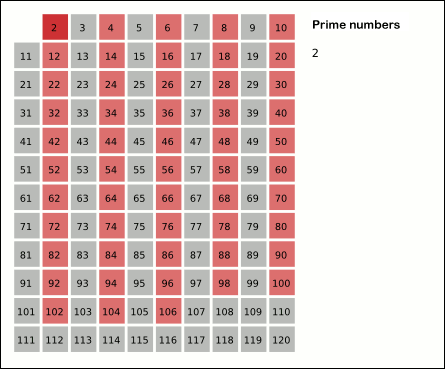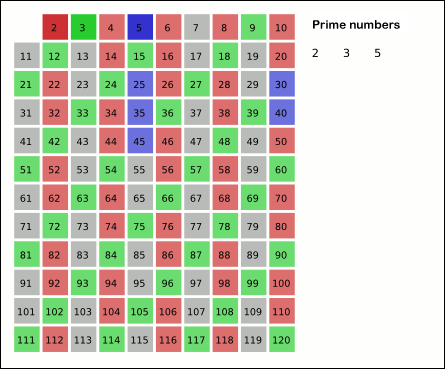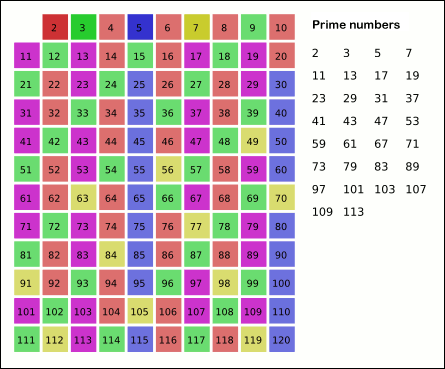
Sieve Of Eratosthenes
In mathematics, the sieve of Eratosthenes is an ancient algorithm for finding all prime numbers up to any given limit. It does so by iteratively marking as composite number, composite (i.e., not prime) the multiples of each prime, starting with the first prime number, 2. The multiples of a given prime are generated as a sequence of numbers starting from that prime, with arithmetic progression, constant difference between them that is equal to that prime.Horsley, Rev. Samuel, F. R. S., "' or, The Sieve of Eratosthenes. Being an account of his method of finding all the Prime Numbers,''Philosophical Transactions'' (1683–1775), Vol. 62. (1772), pp. 327–347 This is the sieve's key distinction from using trial division to sequentially test each candidate number for divisibility by each prime. Once all the multiples of each discovered prime have been marked as composites, the remaining unmarked numbers are primes. The earliest known reference to the sieve (, ''kóskinon Eratosthén ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |