|
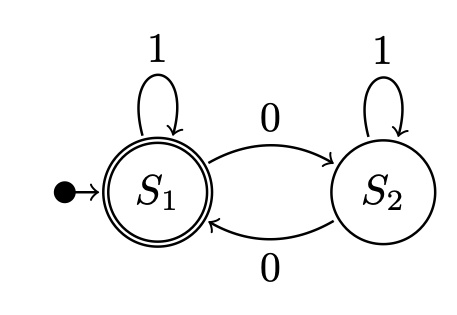
Transition Monoid
In mathematics and theoretical computer science, a semiautomaton is a deterministic finite automaton having inputs but no output. It consists of a set ''Q'' of states, a set Σ called the input alphabet, and a function ''T'': ''Q'' × Σ → ''Q'' called the transition function. Associated with any semiautomaton is a monoid called the characteristic monoid, input monoid, transition monoid or transition system of the semiautomaton, which acts on the set of states ''Q''. This may be viewed either as an action of the free monoid of strings in the input alphabet Σ, or as the induced transformation semigroup of ''Q''. In older books like Clifford and Preston (1967) semigroup actions are called "operands". In category theory, semiautomata essentially are functors. Transformation semigroups and monoid acts : A transformation semigroup or transformation monoid is a pair (M,Q) consisting of a set ''Q'' (often called the "set of states") and a semigroup or monoid ''M'' of functions, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Associative
In mathematics, the associative property is a property of some binary operations that rearranging the parentheses in an expression will not change the result. In propositional logic, associativity is a valid rule of replacement for expressions in logical proofs. Within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operands is not changed. That is (after rewriting the expression with parentheses and in infix notation if necessary), rearranging the parentheses in such an expression will not change its value. Consider the following equations: \begin (2 + 3) + 4 &= 2 + (3 + 4) = 9 \,\\ 2 \times (3 \times 4) &= (2 \times 3) \times 4 = 24 . \end Even though the parentheses were rearranged on each line, the values of the expressions were not altered. Since this holds true when performing addition and multiplication on any real numbers, i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Finite Automata
In physics, a quantum (: quanta) is the minimum amount of any physical entity (physical property) involved in an interaction. The fundamental notion that a property can be "quantized" is referred to as "the hypothesis of quantization". This means that the magnitude of the physical property can take on only discrete values consisting of integer multiples of one quantum. For example, a photon is a single quantum of light of a specific frequency (or of any other form of electromagnetic radiation). Similarly, the energy of an electron bound within an atom is quantized and can exist only in certain discrete values. Atoms and matter in general are stable because electrons can exist only at discrete energy levels within an atom. Quantization is one of the foundations of the much broader physics of quantum mechanics. Quantization of energy and its influence on how energy and matter interact (quantum electrodynamics) is part of the fundamental framework for understanding and describing ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
De Bruijn Graph
In graph theory, an -dimensional De Bruijn graph of symbols is a directed graph representing overlaps between sequences of symbols. It has vertices, consisting of all possible sequences of the given symbols; the same symbol may appear multiple times in a sequence. For a set of symbols the set of vertices is: :V=S^n=\. If one of the vertices can be expressed as another vertex by shifting all its symbols by one place to the left and adding a new symbol at the end of this vertex, then the latter has a directed edge to the former vertex. Thus the set of arcs (that is, directed edges) is :E=\. Although De Bruijn graphs are named after Nicolaas Govert de Bruijn, they were invented independently by both de Bruijn and I. J. Good. Much earlier, Camille Flye Sainte-Marie implicitly used their properties. Properties * If , then the condition for any two vertices forming an edge holds vacuously, and hence all the vertices are connected, forming a total of edges. * Each vertex has e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
State Transition Table
In automata theory and sequential logic, a state-transition table is a table showing what state (or states in the case of a nondeterministic finite automaton) a finite-state machine will move to, based on the current state and other inputs. It is essentially a truth table in which the inputs include the current state along with other inputs, and the outputs include the next state along with other outputs. A state-transition table is one of many ways to specify a finite-state machine. Other ways include a state diagram. Common forms One-dimension State-transition tables are sometimes one-dimensional tables, also called ''characteristic tables''. They are much more like truth tables than their two-dimensional form. The single dimension indicates inputs, current states, next states and (optionally) outputs associated with the state transitions. : Two-dimensions State-transition tables are typically two-dimensional tables. There are two common ways for arranging them. In th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Identity Function
Graph of the identity function on the real numbers In mathematics, an identity function, also called an identity relation, identity map or identity transformation, is a function that always returns the value that was used as its argument, unchanged. That is, when is the identity function, the equality is true for all values of to which can be applied. Definition Formally, if is a set, the identity function on is defined to be a function with as its domain and codomain, satisfying In other words, the function value in the codomain is always the same as the input element in the domain . The identity function on is clearly an injective function as well as a surjective function (its codomain is also its range), so it is bijective. The identity function on is often denoted by . In set theory, where a function is defined as a particular kind of binary relation, the identity function is given by the identity relation, or ''diagonal'' of . Algebraic propert ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Empty Word
In formal language theory, the empty string, or empty word, is the unique string of length zero. Formal theory Formally, a string is a finite, ordered sequence of characters such as letters, digits or spaces. The empty string is the special case where the sequence has length zero, so there are no symbols in the string. There is only one empty string, because two strings are only different if they have different lengths or a different sequence of symbols. In formal treatments, the empty string is denoted with ε or sometimes Λ or λ. The empty string should not be confused with the empty language ∅, which is a formal language (i.e. a set of strings) that contains no strings, not even the empty string. The empty string has several properties: * , ε, = 0. Its string length is zero. * ε ⋅ s = s ⋅ ε = s. The empty string is the identity element of the concatenation operation. The set of all strings forms a free monoid with respect to ⋅ and ε. * εR = ε. Reversal o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kleene Star
In mathematical logic and theoretical computer science, the Kleene star (or Kleene operator or Kleene closure) is a unary operation on a Set (mathematics), set to generate a set of all finite-length strings that are composed of zero or more repetitions of members from . It was named after American mathematician Stephen Cole Kleene, who first introduced and widely used it to characterize Automata theory, automata for regular expressions. In mathematics, it is more commonly known as the free monoid construction. Definition Given a set V, define :V^=\ (the set consists only of the empty string), :V^=V, and define recursively the set :V^=\ for each i>0. V^i is called the i-th power of V, it is a shorthand for the Concatenation#Concatenation of sets of strings, concatenation of V by itself i times. That is, ''V^i'' can be understood to be the set of all strings that can be represented as the concatenation of i members from V. The definition of Kleene star on V is : V^*=\bigcup_V^i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Alphabet (computer Science)
In formal language theory, an alphabet, sometimes called a vocabulary, is a non-empty set of indivisible symbols/ characters/glyphs, typically thought of as representing letters, characters, digits, phonemes, or even words. The definition is used in a diverse range of fields including logic, mathematics, computer science, and linguistics. An alphabet may have any cardinality ("size") and, depending on its purpose, may be finite (e.g., the alphabet of letters "a" through "z"), countable (e.g., \), or even uncountable (e.g., \). Strings, also known as "words" or "sentences", over an alphabet are defined as a sequence of the symbols from the alphabet set. For example, the alphabet of lowercase letters "a" through "z" can be used to form English words like "iceberg" while the alphabet of both upper and lower case letters can also be used to form proper names like "Wikipedia". A common alphabet is , the binary alphabet, and a "00101111" is an example of a binary string. Infinite se ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Finite-state Machine
A finite-state machine (FSM) or finite-state automaton (FSA, plural: ''automata''), finite automaton, or simply a state machine, is a mathematical model of computation. It is an abstract machine that can be in exactly one of a finite number of ''State (computer science), states'' at any given time. The FSM can change from one state to another in response to some Input (computer science), inputs; the change from one state to another is called a ''transition''. An FSM is defined by a list of its states, its initial state, and the inputs that trigger each transition. Finite-state machines are of two types—Deterministic finite automaton, deterministic finite-state machines and Nondeterministic finite automaton, non-deterministic finite-state machines. For any non-deterministic finite-state machine, an equivalent deterministic one can be constructed. The behavior of state machines can be observed in many devices in modern society that perform a predetermined sequence of actions d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Category (mathematics)
In mathematics, a category (sometimes called an abstract category to distinguish it from a concrete category) is a collection of "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose objects are sets and whose arrows are functions. ''Category theory'' is a branch of mathematics that seeks to generalize all of mathematics in terms of categories, independent of what their objects and arrows represent. Virtually every branch of modern mathematics can be described in terms of categories, and doing so often reveals deep insights and similarities between seemingly different areas of mathematics. As such, category theory provides an alternative foundation for mathematics to set theory and other proposed axiomatic foundations. In general, the objects and arrows may be abstract entities of any kind, and the n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |