|
Torsion
Torsion may refer to: Science * Torsion (mechanics), the twisting of an object due to an applied torque * Torsion of spacetime, the field used in Einstein–Cartan theory and ** Alternatives to general relativity * Torsion angle, in chemistry Biology and medicine * Torsion fracture or spiral fracture, a bone fracture when torque is applied * Organ torsion, twisting that interrupts the blood supply to that organ: ** Splenic torsion, causing splenic infarction ** Ovarian torsion ** Testicular torsion * Penile torsion, a congenital condition * Torsion of the digestive tract in some domestic animals: ** Torsion, a type of horse colic ** Gastric torsion, or gastric dilatation volvulus * Torsion (gastropod), a developmental feature of all gastropods Mathematics * Torsion of a curve * Torsion tensor, in differential geometry * Torsion (algebra), in ring theory * Torsion group, in group theory and arithmetic geometry * Tor functor, the derived functors of the tensor product of modules ove ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Testicular Torsion
Testicular torsion occurs when the spermatic cord (from which the testicle is suspended) twists, cutting off the blood supply to the testicle. The most common symptom in children is sudden, severe testicular pain. The testicle may be higher than usual in the scrotum and vomiting may occur. In newborns, pain is often absent and instead the scrotum may become discolored or the testicle may disappear from its usual place. Most of those affected have no obvious prior underlying health problems. Testicular tumor or prior trauma may increase risk. Other risk factors include a congenital malformation known as a "bell-clapper deformity" wherein the testis is inadequately attached to the scrotum allowing it to move more freely and thus potentially twist. Cold temperatures may also be a risk factor. The diagnosis should usually be made based on the presenting symptoms, but requires timely diagnosis and treatment to avoid testicular loss. An ultrasound can be useful when the diagnosis is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Torsion (algebra)
In mathematics, specifically in ring theory, a torsion element is an element of a module that yields zero when multiplied by some non-zero-divisor of the ring. The torsion submodule of a module is the submodule formed by the torsion elements. A torsion module is a module that equals its torsion submodule. A module is torsion-free if its torsion submodule comprises only the zero element. This terminology is more commonly used for modules over a domain, that is, when the regular elements of the ring are all its nonzero elements. This terminology applies to abelian groups (with "module" and "submodule" replaced by " group" and "subgroup"). This is allowed by the fact that the abelian groups are the modules over the ring of integers (in fact, this is the origin of the terminology, that has been introduced for abelian groups before being generalized to modules). In the case of groups that are noncommutative, a ''torsion element'' is an element of finite order. Contrary to the c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Torsion Tensor
In differential geometry, the notion of torsion is a manner of characterizing a twist or screw of a moving frame around a curve. The torsion of a curve, as it appears in the Frenet–Serret formulas, for instance, quantifies the twist of a curve about its tangent vector as the curve evolves (or rather the rotation of the Frenet–Serret frame about the tangent vector). In the geometry of surfaces, the ''geodesic torsion'' describes how a surface twists about a curve on the surface. The companion notion of curvature measures how moving frames "roll" along a curve "without twisting". More generally, on a differentiable manifold equipped with an affine connection (that is, a connection in the tangent bundle), torsion and curvature form the two fundamental invariants of the connection. In this context, torsion gives an intrinsic characterization of how tangent spaces twist about a curve when they are parallel transported; whereas curvature describes how the tangent spaces r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Einstein–Cartan Theory
In theoretical physics, the Einstein–Cartan theory, also known as the Einstein–Cartan–Sciama–Kibble theory, is a classical theory of gravitation similar to general relativity. The theory was first proposed by Élie Cartan in 1922. Einstein–Cartan theory is the simplest Poincaré gauge theory. Overview Einstein–Cartan theory differs from general relativity in two ways: (1) it is formulated within the framework of Riemann–Cartan geometry, which possesses a locally gauged Lorentz symmetry, while general relativity is formulated within the framework of Riemannian geometry, which does not; (2) an additional set of equations are posed that relate torsion to spin. This difference can be factored into by first reformulating general relativity onto a Riemann–Cartan geometry, replacing the Einstein–Hilbert action over Riemannian geometry by the Palatini action over Riemann–Cartan geometry; and second, removing the zero torsion constraint from the Palatini action, whic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Analytic Torsion
In mathematics, Reidemeister torsion (or R-torsion, or Reidemeister–Franz torsion) is a topological invariant of manifolds introduced by Kurt Reidemeister for 3-manifolds and generalized to higher dimensions by and . Analytic torsion (or Ray–Singer torsion) is an invariant of Riemannian manifolds defined by as an analytic analogue of Reidemeister torsion. and proved Ray and Singer's conjecture that Reidemeister torsion and analytic torsion are the same for compact Riemannian manifolds. Reidemeister torsion was the first invariant in algebraic topology that could distinguish between closed manifolds which are homotopy equivalent but not homeomorphic, and can thus be seen as the birth of geometric topology as a distinct field. It can be used to classify lens spaces. Reidemeister torsion is closely related to Whitehead torsion; see . It has also given some important motivation to arithmetic topology; see . For more recent work on torsion see the books and . Definition o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ovarian Torsion
Ovarian torsion (OT) or adnexal torsion is an abnormal condition where an ovary twists on its attachment to other structures, such that blood flow is decreased. Symptoms typically include pelvic pain on one side. While classically the pain is sudden in onset, this is not always the case. Other symptoms may include nausea. Complications may include infection, bleeding, or infertility. Risk factors include ovarian cysts, ovarian enlargement, ovarian tumors, pregnancy, fertility treatment, and prior tubal ligation. The diagnosis may be supported by an ultrasound done via the vagina or CT scan, but these do not completely rule out the diagnosis. Surgery is the most accurate method of diagnosis. Treatment is by surgery to either untwist and fix the ovary in place or to remove it. The ovary will often recover, even if the condition has been present for some time. In those who have had a prior ovarian torsion, there is a 10% chance the other will also be affected. The diagnosis is re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Torsion-free Module
In algebra, a torsion-free module is a module over a ring such that zero is the only element annihilated by a regular element (non zero-divisor) of the ring. In other words, a module is ''torsion free'' if its torsion submodule is reduced to its zero element. In integral domains the regular elements of the ring are its nonzero elements, so in this case a torsion-free module is one such that zero is the only element annihilated by some non-zero element of the ring. Some authors work only over integral domains and use this condition as the definition of a torsion-free module, but this does not work well over more general rings, for if the ring contains zero-divisors then the only module satisfying this condition is the zero module. Examples of torsion-free modules Over a commutative ring ''R'' with total quotient ring ''K'', a module ''M'' is torsion-free if and only if Tor1(''K''/''R'',''M'') vanishes. Therefore flat modules, and in particular free and projective modules, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Torsion (gastropod)
Torsion is a gastropod synapomorphy which occurs in all gastropods during larval development. Torsion is the rotation of the visceral mass, mantle, and shell 180˚ with respect to the head and foot of the gastropod. This rotation brings the mantle cavity and the anus to an anterior position above the head. In some groups of gastropods (Opisthobranchia) there is a degree of secondary detorsion or rotation towards the original position; this may be only partial detorsion or full detorsion. The torsion or twisting of the visceral mass of larval gastropods is not the same thing as the spiral coiling of the shell, which is also present in many shelled gastropods. Development There are two different developmental stages which cause torsion. The first stage is caused by the development of the asymmetrical velar/foot muscle which has one end attached to the left side of the shell and the other end has fibres attached to the left side of the foot and head. At a certain point in larva ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
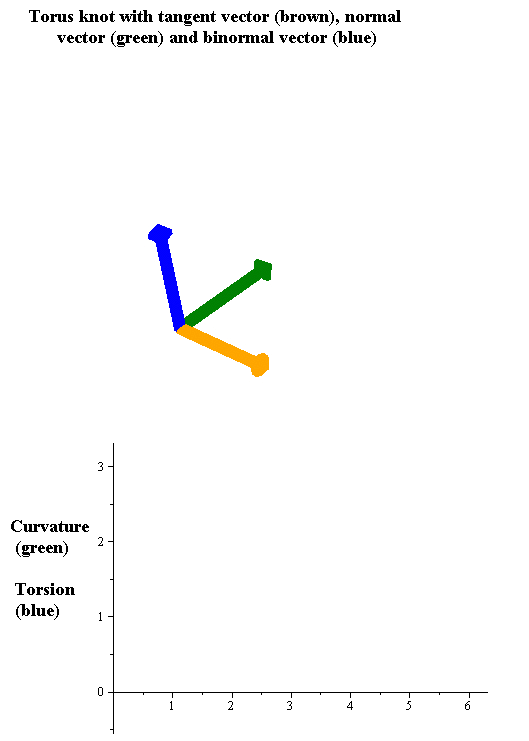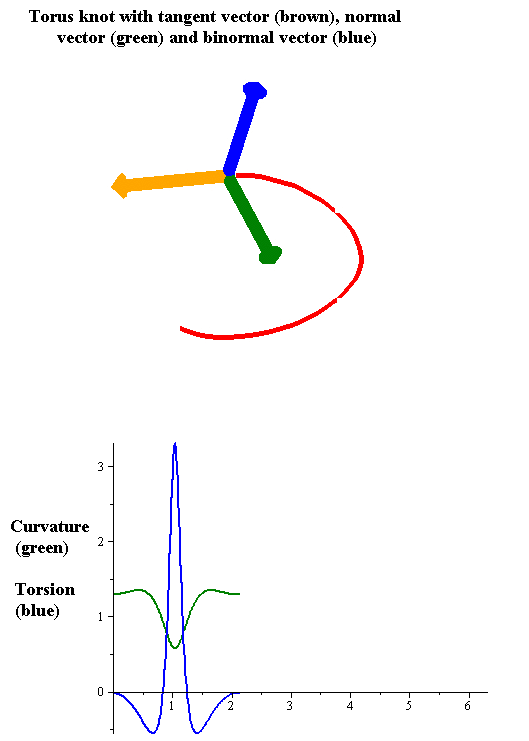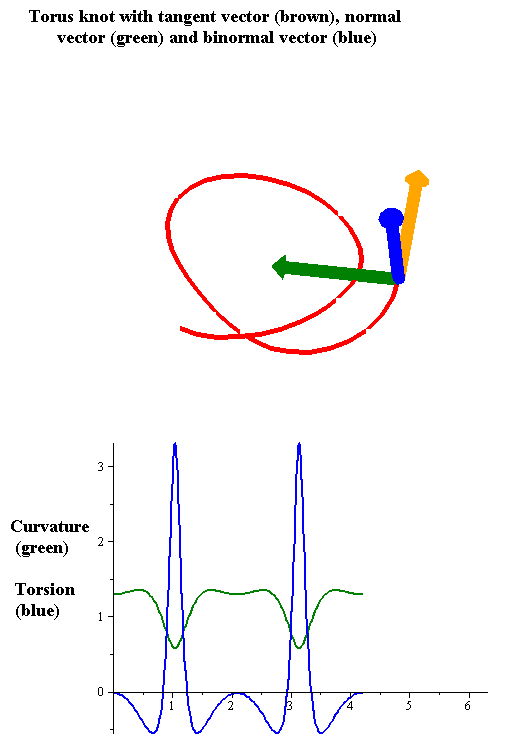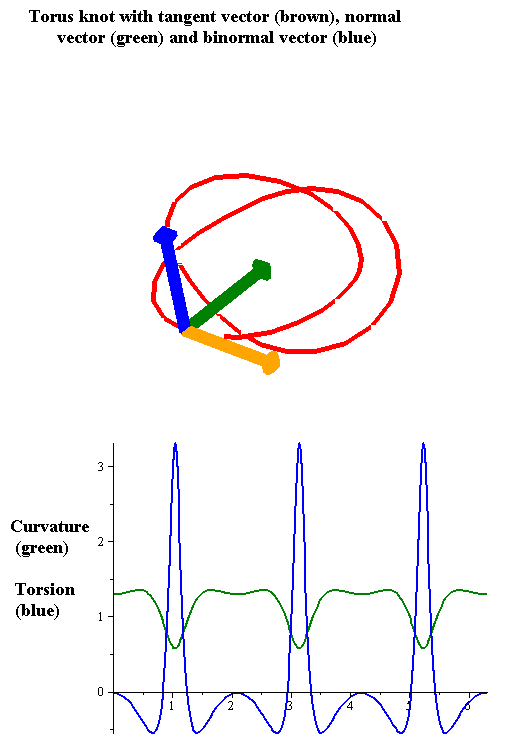
Torsion Of A Curve
In the differential geometry of curves in three dimensions, the torsion of a curve measures how sharply it is twisting out of the osculating plane. Taken together, the curvature and the torsion of a space curve are analogous to the curvature of a plane curve. For example, they are coefficients in the system of differential equations for the Frenet frame given by the Frenet–Serret formulas. Definition Let be a space curve parametrized by arc length and with the unit tangent vector . If the curvature of at a certain point is not zero then the principal normal vector and the binormal vector at that point are the unit vectors : \mathbf=\frac, \quad \mathbf=\mathbf\times\mathbf respectively, where the prime denotes the derivative of the vector with respect to the parameter . The torsion measures the speed of rotation of the binormal vector at the given point. It is found from the equation : \mathbf' = -\tau\mathbf. which means : \tau = -\mathbf\cdot\mathb ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Whitehead Torsion
In geometric topology, a field within mathematics, the obstruction to a homotopy equivalence f\colon X \to Y of finite CW-complexes being a simple homotopy equivalence is its Whitehead torsion \tau(f) which is an element in the Whitehead group \operatorname(\pi_1(Y)). These concepts are named after the mathematician J. H. C. Whitehead. The Whitehead torsion is important in applying surgery theory to non-simply connected manifolds of dimension > 4: for simply-connected manifolds, the Whitehead group vanishes, and thus homotopy equivalences and simple homotopy equivalences are the same. The applications are to differentiable manifolds, PL manifolds and topological manifolds. The proofs were first obtained in the early 1960s by Stephen Smale, for differentiable manifolds. The development of handlebody theory allowed much the same proofs in the differentiable and PL categories. The proofs are much harder in the topological category, requiring the theory of Robion Kirby an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Torsion (mechanics)
In the field of solid mechanics, torsion is the twisting of an object due to an applied torque. Torsion is expressed in either the pascal (Pa), an SI unit for newtons per square metre, or in pounds per square inch (psi) while torque is expressed in newton metres (N·m) or foot-pound force (ft·lbf). In sections perpendicular to the torque axis, the resultant shear stress in this section is perpendicular to the radius. In non-circular cross-sections, twisting is accompanied by a distortion called warping, in which transverse sections do not remain plane. For shafts of uniform cross-section unrestrained against warping, the torsion is: : T = \frac \tau= \frac G \varphi where: * ''T'' is the applied torque or moment of torsion in Nm. * \tau (tau) is the maximum shear stress at the outer surface * ''J''T is the torsion constant for the section. For circular rods, and tubes with constant wall thickness, it is equal to the polar moment of inertia of the section, but for other s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Penile Torsion
Penile torsion is a fairly common congenital condition with male infants. It occurs up to about 1 in 80 newborn males. With this condition, the penis appears rotated on its axis, almost always to the left (counterclockwise). See also * Chordee References {{Reflist * Bar-Yosef Y, Binyamini J, Matzkin H, Ben-Chaim J. Degloving and realignment—simple repair of isolated penile torsion. Urology 2007 Feb;69(2):369-71. * Bauer R, Kogan BA. Modern technique for penile torsion repair. J Urol. 2009 Jul;182(1):286-90 * Snow BW. Penile torsion correction by diagonal corporal plication sutures. Int Braz J Urol. 2009 Jan-Feb;35(1):56-9 * Abdelhamid A, Zeid A, Soliman H. Penile torsion: An overlooked anomaly with distal hypospadias. Annals of Pediatric Surgery 2010 Apr; 6(2)93-97. * Wilcox D, Godbole P, Cooper C.Pediatric Urology Book External links Penile torsion image Congenital disorders of male genital organs ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
.jpg)