|
Thermoacoustics
Thermoacoustics is the interaction between temperature, density and pressure variations of acoustic waves. Thermoacoustic heat engines can readily be driven using solar energy or waste heat and they can be controlled using proportional control. They can use heat available at low temperatures which makes it ideal for heat recovery and low power applications. The components included in thermoacoustic engines are usually very simple compared to conventional engines. The device can easily be controlled and maintained. Thermoacoustic effects can be observed when partly molten glass tubes connected to glass vessels. Sometimes spontaneously a loud and monotone sound is produced. A similar effect is observed if one side of a stainless steel tube is at room temperature (293 K) and the other side is in contact with liquid helium at 4.2 K. In this case, spontaneous oscillations are observed which are named "Taconis oscillations". The mathematical foundation of thermoacoustic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Thermoacoustic Heat Engine
Thermoacoustic engines (sometimes called "TA engines") are thermoacoustic devices which use high-amplitude sound waves to pump heat from one place to another (this requires work, which is provided by the loudspeaker) or use a heat difference to produce work in the form of sound waves (these waves can then be converted into electrical current the same way as a microphone does). These devices can be designed to use either a standing wave or a travelling wave. Compared to vapor refrigerators, thermoacoustic refrigerators have no coolant and few moving parts (only the loudspeaker), therefore require no dynamic sealing or lubrication. History The ability of heat to produce sound was noted by glassblowers centuries ago. In the 1850s experiments showed that a temperature differential drove the phenomenon, and that acoustic volume and intensity vary with tube length and bulb size. Rijke demonstrated that adding a heated wire screen a quarter of the way up the tube greatly mag ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rijke Tube
The Rijke tube is a cylindrical tube with both ends open, inside of which a heat source is placed that turns heat into sound, by creating a self-amplifying standing wave. It is an entertaining phenomenon in acoustics and is an excellent example of resonance. Discovery P. L. Rijke was a professor of physics at the Leiden University in the Netherlands when, in 1859, he discovered a way of using heat to sustain a sound in a cylindrical tube open at both ends. He used a glass tube, about 0.8 m long and 3.5 cm in diameter. Inside it, about 20 cm from one end, he placed a disc of wire gauze as shown in the figure on right. Friction with the walls of the tube is sufficient to keep the gauze in position. With the tube vertical and the gauze in the lower half, he heated the gauze with a flame until it was glowing red hot. Upon removing the flame, he obtained a loud sound from the tube which lasted until the gauze cooled down (about 10 s). It is safer in modern reproducti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
John William Strutt, 3rd Baron Rayleigh
John William Strutt, 3rd Baron Rayleigh, (; 12 November 1842 – 30 June 1919) was an English mathematician and physicist who made extensive contributions to science. He spent all of his academic career at the University of Cambridge. Among many honors, he received the 1904 Nobel Prize in Physics "for his investigations of the densities of the most important gases and for his discovery of argon in connection with these studies." He served as president of the Royal Society from 1905 to 1908 and as chancellor of the University of Cambridge from 1908 to 1919. Rayleigh provided the first theoretical treatment of the elastic scattering of light by particles much smaller than the light's wavelength, a phenomenon now known as " Rayleigh scattering", which notably explains why the sky is blue. He studied and described transverse surface waves in solids, now known as " Rayleigh waves". He contributed extensively to fluid dynamics, with concepts such as the Rayleigh number (a dimen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Acoustic Wave
Acoustic waves are a type of energy propagation through a medium by means of adiabatic loading and unloading. Important quantities for describing acoustic waves are acoustic pressure, particle velocity, particle displacement and acoustic intensity. Acoustic waves travel with a characteristic acoustic velocity that depends on the medium they're passing through. Some examples of acoustic waves are audible sound from a speaker (waves traveling through air at the speed of sound), seismic waves (ground vibrations traveling through the earth), or ultrasound used for medical imaging (waves traveling through the body). Wave properties Acoustic wave equation The acoustic wave equation describes the propagation of sound waves. The acoustic wave equation for sound pressure in one dimension is given by - = 0 where *p is sound pressure in Pa *x is position in the direction of propagation of the wave, in m *c is speed of sound in m/s *t is time in s The wave equation for particl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
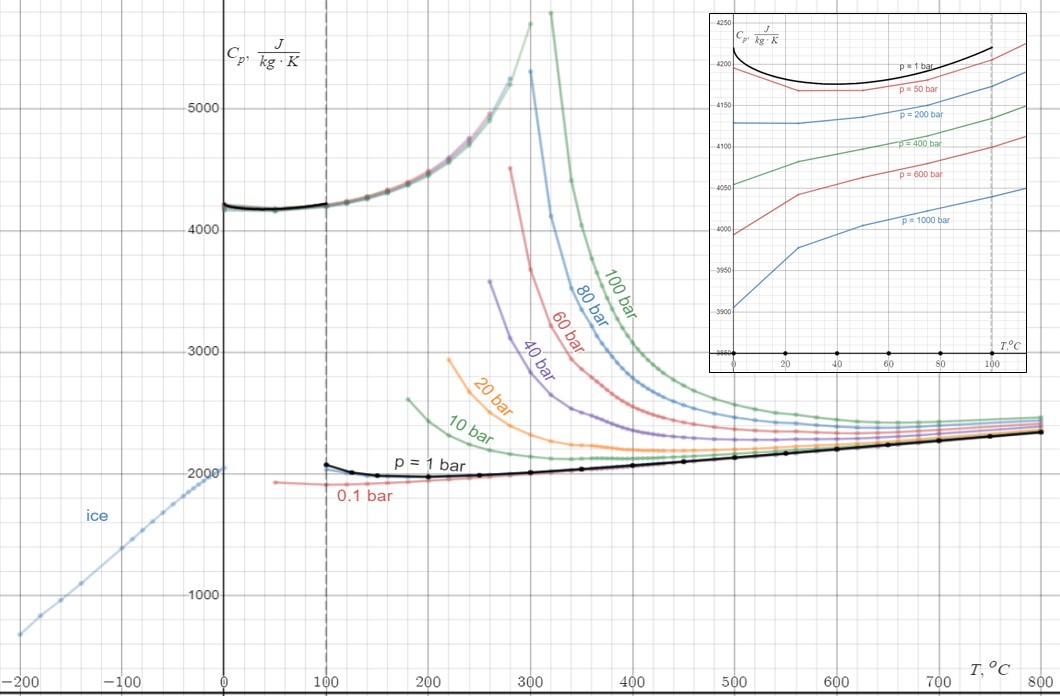
Heat Capacity
Heat capacity or thermal capacity is a physical property of matter, defined as the amount of heat to be supplied to an object to produce a unit change in its temperature. The SI unit of heat capacity is joule per kelvin (J/K). Heat capacity is an extensive property. The corresponding intensive property is the specific heat capacity, found by dividing the heat capacity of an object by its mass. Dividing the heat capacity by the amount of substance in moles yields its molar heat capacity. The volumetric heat capacity measures the heat capacity per volume. In architecture and civil engineering, the heat capacity of a building is often referred to as its thermal mass. Definition Basic definition The heat capacity of an object, denoted by C, is the limit : C = \lim_\frac, where \Delta Q is the amount of heat that must be added to the object (of mass ''M'') in order to raise its temperature by \Delta T. The value of this parameter usually varies considerably dependin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Power (physics)
In physics, power is the amount of energy transferred or converted per unit time. In the International System of Units, the unit of power is the watt, equal to one joule per second. In older works, power is sometimes called ''activity''. Power is a Scalar (physics), scalar quantity. Power is related to other quantities; for example, the power involved in moving a ground vehicle is the product of the aerodynamic drag plus traction (engineering), traction force on the wheels, and the velocity of the vehicle. The output power of a Engine, motor is the product of the torque that the motor generates and the angular velocity of its output shaft. Likewise, the power dissipated in an electrical element of a electrical circuit, circuit is the product of the electric current, current flowing through the element and of the voltage across the element. Definition Power is the rate with respect to time at which work is done; it is the time derivative of Work (physics), work: P =\frac where ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Amplitude
The amplitude of a periodic variable is a measure of its change in a single period (such as time or spatial period). The amplitude of a non-periodic signal is its magnitude compared with a reference value. There are various definitions of amplitude (see below), which are all functions of the magnitude of the differences between the variable's extreme values. In older texts, the phase of a periodic function is sometimes called the amplitude. Definitions Peak amplitude & semi-amplitude For symmetric periodic waves, like sine wave A sine wave, sinusoidal wave, or just sinusoid is a curve, mathematical curve defined in terms of the ''sine'' trigonometric function, of which it is the graph of a function, graph. It is a type of continuous wave and also a Smoothness, smooth p ...s, square waves or triangle waves ''peak amplitude'' and ''semi amplitude'' are the same. Peak amplitude In audio system measurements, telecommunications and others where the wikt:measurand, measu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Standing Wave
In physics, a standing wave, also known as a stationary wave, is a wave that oscillates in time but whose peak amplitude profile does not move in space. The peak amplitude of the wave oscillations at any point in space is constant with respect to time, and the oscillations at different points throughout the wave are in phase. The locations at which the absolute value of the amplitude is minimum are called nodes, and the locations where the absolute value of the amplitude is maximum are called antinodes. Standing waves were first noticed by Michael Faraday in 1831. Faraday observed standing waves on the surface of a liquid in a vibrating container. Franz Melde coined the term "standing wave" (German: ''stehende Welle'' or ''Stehwelle'') around 1860 and demonstrated the phenomenon in his classic experiment with vibrating strings. This phenomenon can occur because the medium is moving in the direction opposite to the movement of the wave, or it can arise in a stationary me ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wave Equation
The (two-way) wave equation is a second-order linear partial differential equation for the description of waves or standing wave fields — as they occur in classical physics — such as mechanical waves (e.g. water waves, sound waves and seismic waves) or electromagnetic waves (including light waves). It arises in fields like acoustics, electromagnetism, and fluid dynamics. Single mechanical or electromagnetic waves propagating in a pre-defined direction can also be described with the first-order one-way wave equation which is much easier to solve and also valid for inhomogenious media. Introduction The (two-way) wave equation is a second-order partial differential equation describing waves, including traveling and standing waves; the latter can be considered as linear superpositions of waves traveling in opposite directions. This article mostly focuses on the scalar wave equation describing waves in scalars by scalar functions of a time variable (a variable repres ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Angular Frequency
In physics, angular frequency "''ω''" (also referred to by the terms angular speed, circular frequency, orbital frequency, radian frequency, and pulsatance) is a scalar measure of rotation rate. It refers to the angular displacement per unit time (for example, in rotation) or the rate of change of the phase of a sinusoidal waveform (for example, in oscillations and waves), or as the rate of change of the argument of the sine function. Angular frequency (or angular speed) is the magnitude of the pseudovector quantity angular velocity.(UP1) One turn is equal to 2''π'' radians, hence \omega = \frac = , where: *''ω'' is the angular frequency (unit: radians per second), *''T'' is the period (unit: seconds), *''f'' is the ordinary frequency (unit: hertz) (sometimes ''ν''). Units In SI units, angular frequency is normally presented in radians per second, even when it does not express a rotational value. The unit hertz (Hz) is dimensionally equivalent, but by conven ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Plane Waves
In physics, a plane wave is a special case of wave or field: a physical quantity whose value, at any moment, is constant through any plane that is perpendicular to a fixed direction in space. For any position \vec x in space and any time t, the value of such a field can be written as :F(\vec x,t) = G(\vec x \cdot \vec n, t), where \vec n is a unit-length vector, and G(d,t) is a function that gives the field's value as dependent on only two real parameters: the time t, and the scalar-valued displacement d = \vec x \cdot \vec n of the point \vec x along the direction \vec n. The displacement is constant over each plane perpendicular to \vec n. The values of the field F may be scalars, vectors, or any other physical or mathematical quantity. They can be complex numbers, as in a complex exponential plane wave. When the values of F are vectors, the wave is said to be a longitudinal wave if the vectors are always collinear with the vector \vec n, and a transverse wave if they ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Molar Mass
In chemistry, the molar mass of a chemical compound is defined as the mass of a sample of that compound divided by the amount of substance which is the number of moles in that sample, measured in moles. The molar mass is a bulk, not molecular, property of a substance. The molar mass is an ''average'' of many instances of the compound, which often vary in mass due to the presence of isotopes. Most commonly, the molar mass is computed from the standard atomic weights and is thus a terrestrial average and a function of the relative abundance of the isotopes of the constituent atoms on Earth. The molar mass is appropriate for converting between the mass of a substance and the amount of a substance for bulk quantities. The molecular mass and formula mass are commonly used as a synonym of molar mass, particularly for molecular compounds; however, the most authoritative sources define it differently. The difference is that molecular mass is the mass of one specific particle or m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |