|
Stiffness To Weight Ratio
Specific modulus is a materials property consisting of the elastic modulus per mass density of a material. It is also known as the stiffness to weight ratio or specific stiffness. High specific modulus materials find wide application in aerospace applications where minimum structural weight is required. The dimensional analysis yields units of distance squared per time squared. The equation can be written as: : \text = E/\rho where E is the elastic modulus and \rho is the density. The utility of specific modulus is to find materials which will produce structures with minimum weight, when the primary design limitation is deflection or physical deformation, rather than load at breaking—this is also known as a "stiffness-driven" structure. Many common structures are stiffness-driven over much of their use, such as airplane wings, bridges, masts, and bicycle frames. To emphasize the point, consider the issue of choosing a material for building an airplane. Aluminum seems obvio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Materials Property
A material property is an intensive property of a material, i.e., a physical property or chemical property that does not depend on the amount of the material. These quantitative properties may be used as a metric by which the benefits of one material versus another can be compared, thereby aiding in materials selection. A property having a fixed value for a given material or substance is called material constant or constant of matter. (Material constants should not be confused with physical constants, that have a universal character.) A material property may also be a function of one or more independent variables, such as temperature. Materials properties often vary to some degree according to the direction in the material in which they are measured, a condition referred to as anisotropy. Materials properties that relate to different physical phenomena often behave linearly (or approximately so) in a given operating range . Modeling them as linear functions can significantly simp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Buckling
In structural engineering, buckling is the sudden change in shape (Deformation (engineering), deformation) of a structural component under Structural load, load, such as the bowing of a column under Compression (physics), compression or the wrinkling of a plate under Shearing (physics), shear. If a structure is subjected to a gradually increasing load, when the load reaches a critical level, a member may suddenly change shape and the structure and component is said to have ''buckled''. Euler's critical load and Johnson's parabolic formula are used to determine the buckling stress of a column. Buckling may occur even though the Stress (mechanics), stresses that develop in the structure are well below those needed to cause Catastrophic failure, failure in the material of which the structure is composed. Further loading may cause significant and somewhat unpredictable deformations, possibly leading to complete loss of the member's load-carrying capacity. However, if the deformation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rubber
Rubber, also called India rubber, latex, Amazonian rubber, ''caucho'', or ''caoutchouc'', as initially produced, consists of polymers of the organic compound isoprene, with minor impurities of other organic compounds. Types of polyisoprene that are used as natural rubbers are classified as elastomers. Currently, rubber is harvested mainly in the form of the latex from the Hevea brasiliensis, Pará rubber tree (''Hevea brasiliensis'') or others. The latex is a sticky, milky and white colloid drawn off by making incisions in the bark and collecting the fluid in vessels in a process called "tapping". Manufacturers refine this latex into the rubber that is ready for commercial processing. Natural rubber is used extensively in many applications and products, either alone or in combination with other materials. In most of its useful forms, it has a large stretch ratio and high resilience and also is buoyant and water-proof. Industrial demand for rubber-like materials began to out ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Aerogel
Aerogels are a class of manufacturing, synthetic porous ultralight material derived from a gel, in which the liquid component for the gel has been replaced with a gas, without significant collapse of the gel structure. The result is a solid with extremely low density and extremely low thermal conductivity. Aerogels can be made from a variety of chemical compounds. Silica aerogels feel like fragile expanded polystyrene, styrofoam to the touch, while some polymer-based aerogels feel like rigid foams. Aerogels are produced by extracting the liquid component of a gel through supercritical drying or freeze-drying. This allows the liquid to be slowly dried off without causing the solid matrix in the gel to collapse from capillary action, as would happen with conventional evaporation. The first aerogels were produced from silica gels. Kistler's later work involved aerogels based on alumina, Chromium(III) oxide, chromia, and tin dioxide. Carbon aerogels were first developed in the late ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Density
Density (volumetric mass density or specific mass) is the ratio of a substance's mass to its volume. The symbol most often used for density is ''ρ'' (the lower case Greek letter rho), although the Latin letter ''D'' (or ''d'') can also be used: \rho = \frac, where ''ρ'' is the density, ''m'' is the mass, and ''V'' is the volume. In some cases (for instance, in the United States oil and gas industry), density is loosely defined as its weight per unit volume, although this is scientifically inaccurate this quantity is more specifically called specific weight. For a pure substance, the density is equal to its mass concentration. Different materials usually have different densities, and density may be relevant to buoyancy, purity and packaging. Osmium is the densest known element at standard conditions for temperature and pressure. To simplify comparisons of density across different systems of units, it is sometimes replaced by the dimensionless quantity "relative den ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pascal (unit)
The pascal (symbol: Pa) is the unit of pressure in the International System of Units (SI). It is also used to quantify internal pressure, stress, Young's modulus, and ultimate tensile strength. The unit, named after Blaise Pascal, is an SI coherent derived unit defined as one newton per square metre (N/m2). It is also equivalent to 10 barye (10 Ba) in the CGS system. Common multiple units of the pascal are the hectopascal (1 hPa = 100 Pa), which is equal to one millibar, and the kilopascal (1 kPa = 1000 Pa), which is equal to one centibar. The unit of measurement called '' standard atmosphere (atm)'' is defined as . Meteorological observations typically report atmospheric pressure in hectopascals per the recommendation of the World Meteorological Organization, thus a standard atmosphere (atm) or typical sea-level air pressure is about 1013 hPa. Reports in the United States typically use inches of mercury or millibars (hectopascals). In Cana ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Specific Stiffness Of Materials Detail View
Specific may refer to: * Specificity (other) * Specific, a cure or therapy for a specific illness Law * Specific deterrence, focussed on an individual * Specific finding, intermediate verdict used by a jury in determining the final verdict * Specific jurisdiction over an out-of-state party, specific to cases that have a substantial connection to the party's in-state activity * Order of specific performance, court order to perform a specific act Economics, finance, and accounting * Asset specificity, the extent to which the investments made to support a particular transaction have a higher value to that transaction than they would have if they were redeployed for any other purpose * Specific identification (inventories), summing purchase costs of all inventory items * Specific rate duty, duty paid at a specific amount per unit * Specific risk, risk that affects a very small number of assets Psychology * Domain specificity, theory that many aspects of cognition ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Section Modulus
In solid mechanics and structural engineering, section modulus is a geometric property of a given cross-section used in the design of beams or flexural members. Other geometric properties used in design include: area for tension and shear, radius of gyration for compression, and second moment of area and polar second moment of area for stiffness. Any relationship between these properties is highly dependent on the shape in question. There are two types of section modulus, elastic and plastic: * The elastic section modulus is used to calculate a cross-section's resistance to bending within the elastic range, where stress and strain are proportional. * The plastic section modulus is used to calculate a cross-section's capacity to resist bending after yielding has occurred across the entire section. It is used for determining the plastic, or full moment, strength and is larger than the elastic section modulus, reflecting the section's strength beyond the elastic range. Equations ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Flange
A flange is a protruded ridge, lip or rim (wheel), rim, either external or internal, that serves to increase shear strength, strength (as the flange of a steel beam (structure), beam such as an I-beam or a T-beam); for easy attachment/transfer of contact force with another object (as the flange on the end of a pipe (fluid conveyance), pipe, steam cylinder, etc., or on the lens mount of a camera); or for stabilizing and guiding the movements of a machine or its parts (as the inside flange of a railroad car, rail car or tram train wheel, wheel, which keep the wheels from derailment, running off the rail profile, rails). Flanges are often attached using bolts in the pattern of a bolt circle. Flanges play a pivotal role in piping systems by allowing easy access for maintenance, inspection, and modification. They provide a means to connect or disconnect Pipe (fluid conveyance), pipes and equipment without the need for welding, which simplifies installation and reduces downtime during ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Area
Area is the measure of a region's size on a surface. The area of a plane region or ''plane area'' refers to the area of a shape or planar lamina, while '' surface area'' refers to the area of an open surface or the boundary of a three-dimensional object. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat. It is the two-dimensional analogue of the length of a curve (a one-dimensional concept) or the volume of a solid (a three-dimensional concept). Two different regions may have the same area (as in squaring the circle); by synecdoche, "area" sometimes is used to refer to the region, as in a " polygonal area". The area of a shape can be measured by comparing the shape to squares of a fixed size. In the International System of Units (SI), the standard unit of area is the square metre (written as m2), which is the area o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
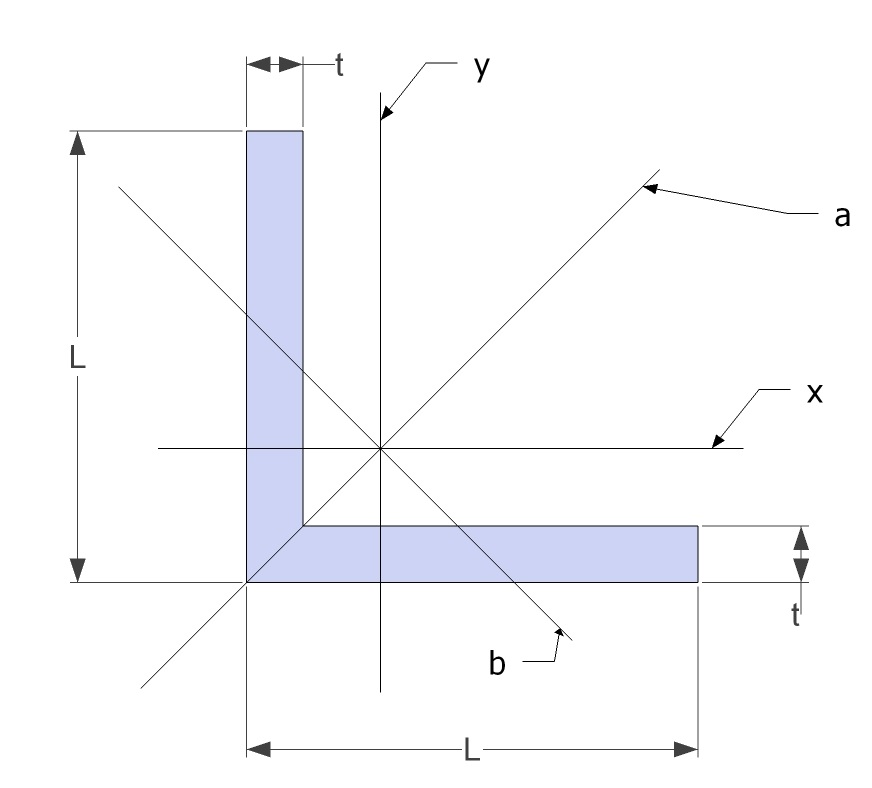
List Of Area Moments Of Inertia
The following is a list of second moments of area of some shapes. The second moment of area, also known as area moment of inertia, is a geometrical property of an area which reflects how its points are distributed with respect to an arbitrary axis. The physical unit, unit of dimension of the second moment of area is length to fourth power, unit of length, L4, and should not be confused with the mass moment of inertia. If the piece is thin, however, the mass moment of inertia equals the area density times the area moment of inertia. Second moments of area Please note that for the second moment of area equations in the below table: I_x = \iint_A y^2 \, dx \, dy and I_y = \iint_A x^2 \, dx \, dy. Parallel axis theorem The parallel axis theorem can be used to determine the second moment of area of a rigid body about any axis, given the body's second moment of area about a parallel axis through the body's centroid, the area of the cross section, and the perpendicular distance ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |