|
Steradians
The steradian (symbol: sr) or square radian is the unit of solid angle in the International System of Units (SI). It is used in three-dimensional geometry, and is analogous to the radian, which quantifies planar angles. A solid angle in the form of a circular cone can be projected onto a sphere from its centre, delineating a spherical cap where the cone intersects the sphere. The magnitude of the solid angle expressed in steradians is defined as the quotient of the surface area of the spherical cap and the square of the sphere's radius. This is analogous to the way a plane angle projected onto a circle delineates a circular arc on the circumference, whose length is proportional to the angle. Steradians can be used to measure a solid angle of any projected shape. The solid angle subtended is the same as that of a cone with the same projected area. A solid angle of one steradian subtends a cone aperture of approximately 1.144 radians or 65.54 degrees. In the SI, solid angle is c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Steradian Cone And Cap
The steradian (symbol: sr) or square radian is the unit of solid angle in the International System of Units (SI). It is used in three-dimensional geometry, and is analogous to the radian, which quantifies planar angles. A solid angle in the form of a circular cone can be projected onto a sphere from its centre, delineating a spherical cap where the cone intersects the sphere. The magnitude of the solid angle expressed in steradians is defined as the quotient of the surface area of the spherical cap and the square of the sphere's radius. This is analogous to the way a plane angle projected onto a circle delineates a circular arc on the circumference, whose length is proportional to the angle. Steradians can be used to measure a solid angle of any projected shape. The solid angle subtended is the same as that of a cone with the same projected area. A solid angle of one steradian subtends a cone aperture of approximately 1.144 radians or 65.54 degrees. In the SI, solid angle is consi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
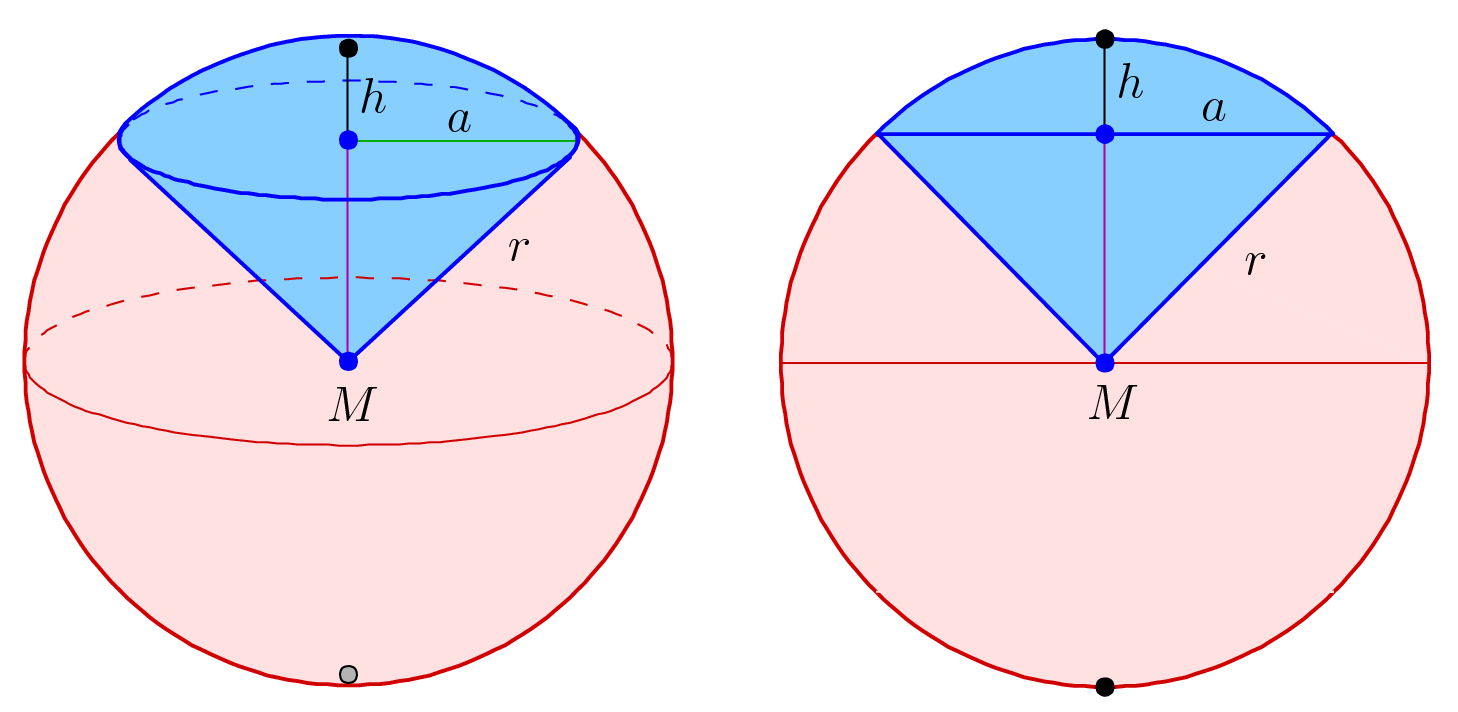
Solid Angle, 1 Steradian
Solid is a state of matter where molecules are closely packed and can not slide past each other. Solids resist compression, expansion, or external forces that would alter its shape, with the degree to which they are resisted dependent upon the specific material under consideration. Solids also always possess the least amount of kinetic energy per atom/molecule relative to other phases or, equivalently stated, solids are formed when matter in the liquid / gas phase is cooled below a certain temperature. This temperature is called the melting point of that substance and is an intrinsic property, i.e. independent of how much of the matter there is. All matter in solids can be arranged on a microscopic scale under certain conditions. Solids are characterized by structural rigidity and resistance to applied external forces and pressure. Unlike liquids, solids do not flow to take on the shape of their container, nor do they expand to fill the entire available volume like a gas. Much ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Particle Beam
A particle beam is a stream of charged particle, charged or neutral particles other than photons. In Particle accelerator, particle accelerators, these particles can move with a velocity close to the speed of light. There is a difference between the creation and control of charged particle beams and neutral particle beams, as only the first type can be manipulated to a sufficient extent by devices based on electromagnetism. The manipulation and diagnostics of charged particle beams at high kinetic energies using particle accelerators are main topics of accelerator physics. Sources Charged particles such as electrons, positrons, and protons may be separated from their common surroundings. This can be accomplished by processes such as thermionic emission or arc discharge. The following devices are commonly used as sources for particle beams: * Ion source * Cathode-ray tube, or more specifically in one of its parts called electron gun. This is also part of traditional television and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Light Beam
A light beam or beam of light is a directional projection of light energy radiating from a light source. Sunlight forms a light beam (a sunbeam) when filtered through media such as clouds, foliage, or windows. To artificially produce a light beam, a lamp and a parabolic reflector is used in many lighting devices such as spotlights, car headlights, PAR Cans, and LED housings. Light from certain types of laser has the smallest possible beam divergence. Visible light beams From the side, a beam of light is only visible if part of the light is scattered by objects: tiny particles like dust, water droplets ( mist, fog, rain), hail, snow, or smoke, or larger objects such as birds. If there are many objects in the light path, then it appears as a continuous beam, but if there are only a few objects, then the light is visible as a few individual bright points. In any case, this scattering of light from a beam, and the resultant visibility of a light beam from the side, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Angle Excess
Spherical trigonometry is the branch of spherical geometry that deals with the metrical relationships between the edge (geometry), sides and angles of spherical triangles, traditionally expressed using trigonometric functions. On the sphere, geodesics are great circles. Spherical trigonometry is of great importance for calculations in astronomy, geodesy, and navigation. The origins of spherical trigonometry in Greek mathematics and the major developments in Islamic mathematics are discussed fully in History of trigonometry and Mathematics in medieval Islam. The subject came to fruition in Early Modern times with important developments by John Napier, Jean Baptiste Joseph Delambre, Delambre and others, and attained an essentially complete form by the end of the nineteenth century with the publication of Todhunter's textbook ''Spherical trigonometry for the use of colleges and Schools''. Since then, significant developments have been the application of vector methods, quaternion m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polygon
In geometry, a polygon () is a plane figure made up of line segments connected to form a closed polygonal chain. The segments of a closed polygonal chain are called its '' edges'' or ''sides''. The points where two edges meet are the polygon's '' vertices'' or ''corners''. An ''n''-gon is a polygon with ''n'' sides; for example, a triangle is a 3-gon. A simple polygon is one which does not intersect itself. More precisely, the only allowed intersections among the line segments that make up the polygon are the shared endpoints of consecutive segments in the polygonal chain. A simple polygon is the boundary of a region of the plane that is called a ''solid polygon''. The interior of a solid polygon is its ''body'', also known as a ''polygonal region'' or ''polygonal area''. In contexts where one is concerned only with simple and solid polygons, a ''polygon'' may refer only to a simple polygon or to a solid polygon. A polygonal chain may cross over itself, creating star polyg ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spat (angular Unit)
The spat (symbol sp), from the Latin ''spatium'' ("space"), is a unit of solid angle. 1 spat is equal to 4 steradians or approximately square degrees of solid angle . Thus it is the solid angle subtended by a complete sphere at its center. The whole sphere contains ~148.510 million square arcminutes and ~534.638 billion square arcseconds. See also * Turn (angle) — the plane angle counterpart of the spat, equivalent to 2 radian The radian, denoted by the symbol rad, is the unit of angle in the International System of Units (SI) and is the standard unit of angular measure used in many areas of mathematics. It is defined such that one radian is the angle subtended at ...s References Units of solid angle {{geometry-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sphere
A sphere (from Ancient Greek, Greek , ) is a surface (mathematics), surface analogous to the circle, a curve. In solid geometry, a sphere is the Locus (mathematics), set of points that are all at the same distance from a given point in three-dimensional space.. That given point is the center (geometry), ''center'' of the sphere, and the distance is the sphere's ''radius''. The earliest known mentions of spheres appear in the work of the Greek mathematics, ancient Greek mathematicians. The sphere is a fundamental surface in many fields of mathematics. Spheres and nearly-spherical shapes also appear in nature and industry. Bubble (physics), Bubbles such as soap bubbles take a spherical shape in equilibrium. The Earth is spherical Earth, often approximated as a sphere in geography, and the celestial sphere is an important concept in astronomy. Manufactured items including pressure vessels and most curved mirrors and lenses are based on spheres. Spheres rolling, roll smoothly in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spherical Sector
In geometry, a spherical sector, also known as a spherical cone, is a portion of a sphere or of a ball defined by a conical boundary with apex at the center of the sphere. It can be described as the union of a spherical cap and the cone formed by the center of the sphere and the base of the cap. It is the three-dimensional analogue of the sector of a circle. Volume If the radius of the sphere is denoted by and the height of the cap by , the volume of the spherical sector is V = \frac\,. This may also be written as V = \frac (1-\cos\varphi)\,, where is half the cone aperture angle, i.e., is the angle between the rim of the cap and the axis direction to the middle of the cap as seen from the sphere center. The limiting case is for approaching 180 degrees, which then describes a complete sphere. The height, is given by h = r (1-\cos\varphi)\,. The volume of the sector is related to the area of the cap by: V = \frac\,. Area The curved surface area of the spherical se ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Surface Area
The surface area (symbol ''A'') of a solid object is a measure of the total area that the surface of the object occupies. The mathematical definition of surface area in the presence of curved surfaces is considerably more involved than the definition of arc length of one-dimensional curves, or of the surface area for polyhedra (i.e., objects with flat polygonal faces), for which the surface area is the sum of the areas of its faces. Smooth surfaces, such as a sphere, are assigned surface area using their representation as parametric surfaces. This definition of surface area is based on methods of infinitesimal calculus and involves partial derivatives and double integration. A general definition of surface area was sought by Henri Lebesgue and Hermann Minkowski at the turn of the twentieth century. Their work led to the development of geometric measure theory, which studies various notions of surface area for irregular objects of any dimension. An important example is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Radius
In classical geometry, a radius (: radii or radiuses) of a circle or sphere is any of the line segments from its Centre (geometry), center to its perimeter, and in more modern usage, it is also their length. The radius of a regular polygon is the line segment or distance from its center to any of its Vertex (geometry), vertices. The name comes from the Latin ''radius'', meaning ray but also the spoke of a chariot wheel.Definition of Radius at dictionary.reference.com. Accessed on 2009-08-08. The typical abbreviation and mathematical symbol for radius is ''R'' or ''r''. By extension, the diameter ''D'' is defined as twice the radius:Definition of radius at mathwords.com. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |