|
Squigonometry
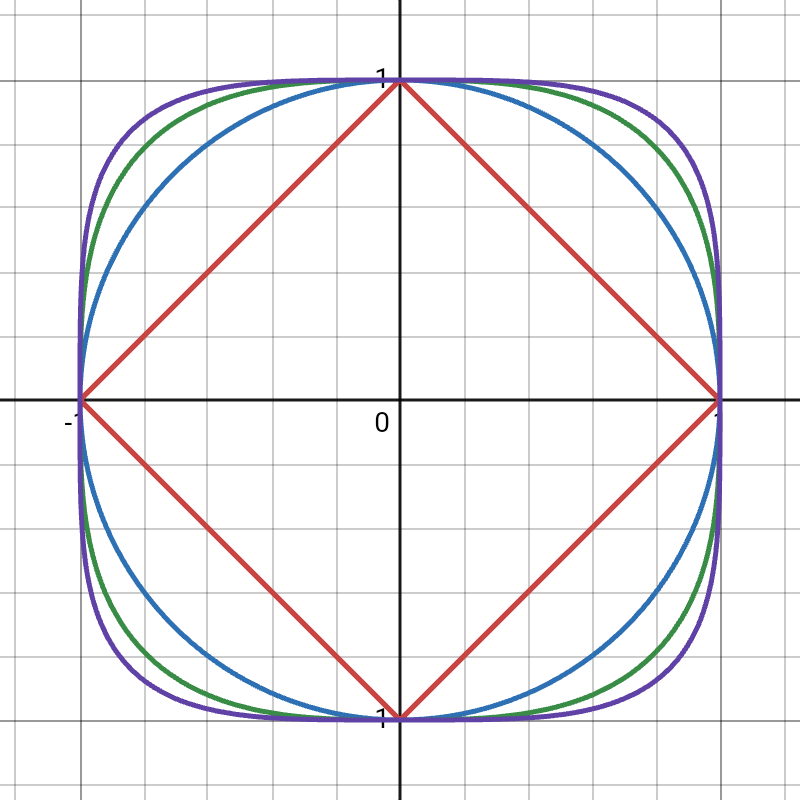
Squigonometry or -trigonometry is a generalization of traditional trigonometry which replaces the circle and Euclidean distance function with the squircle (shape intermediate between a square and circle) and -norm. While trigonometry deals with the relationships between angles and lengths in the plane using trigonometric functions defined relative to a unit circle, squigonometry focuses on analogous relationships and functions within the context of a unit squircle. Etymology The term squigonometry is a portmanteau of ''square'' or ''squircle'' and ''trigonometry''. It was used by Derek Holton to refer to an analog of trigonometry using a square as a basic shape (instead of a circle) in his 1990 pamphlet ''Creating Problems''. In 2011 it was used by William Wood to refer to trigonometry with a squircle as its base shape in a recreational mathematics article in ''Mathematics Magazine''. In 2016 Robert Poodiack extended Wood's work in another ''Mathematics Magazine'' article. Wood ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Superegg
In geometry, a superegg is a solid of revolution obtained by rotating an elongated superellipse with exponent greater than 2 around its longest axis. It is a special case of superellipsoid. Unlike an elongated ellipsoid, an elongated superegg can stand upright on a flat surface, or on top of another superegg. This is due to its curvature being zero at the tips. The shape was popularized by Danish poet and scientist Piet Hein (1905–1996). Supereggs of various materials, including brass, were sold as novelties or " executive toys" in the 1960s. Mathematical description The superegg is a superellipsoid whose horizontal cross-sections are circles. It is defined by the inequality :\left, \frac\^p + \left, \frac\^p \leq 1 \, , where ''R'' is the horizontal radius at the "equator" (the widest part as defined by the circles), and ''h'' is one half of the height. The exponent ''p'' determines the degree of flattening at the tips and equator. Hein's choice was ''p'' = 2.5 (the s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |