|
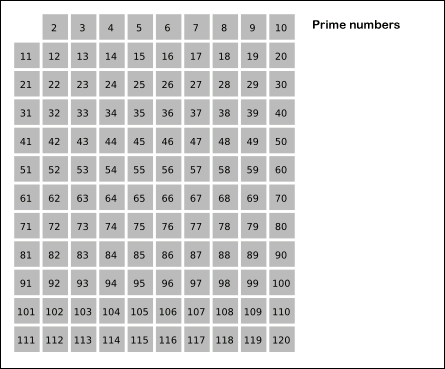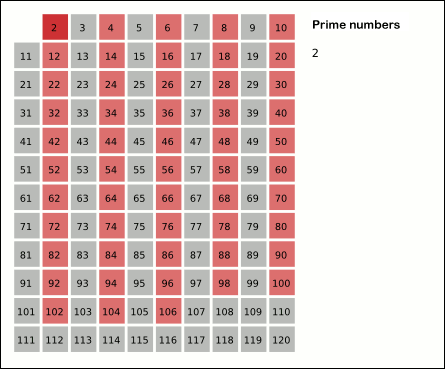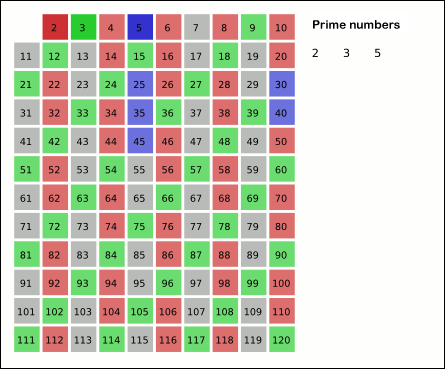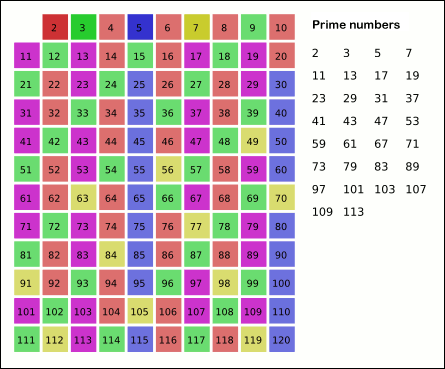
Sieve Of Sundaram
In mathematics, the sieve of Sundaram is a variant of the sieve of Eratosthenes, a simple deterministic algorithm for finding all the prime numbers up to a specified integer. It was discovered by Indian student S. P. Sundaram in 1934. Algorithm The sieve starts with a list of the integers from 1 to . From this list, all numbers of the form are removed, where and are positive integers such that and The remaining numbers are doubled and incremented by one, giving a list of the odd prime numbers (that is, all primes except 2) below The sieve of Sundaram sieves out the composite numbers just as the sieve of Eratosthenes does, but even numbers are not considered; the work of "crossing out" the multiples of 2 is done by the final double-and-increment step. Whenever Eratosthenes' method would cross out different multiples of a prime , Sundaram's method crosses out for Correctness If we start with integers from to , the final list contains only odd integers from to From ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prime-counting Function
In mathematics, the prime-counting function is the function counting the number of prime numbers less than or equal to some real number . It is denoted by (unrelated to the number ). A symmetric variant seen sometimes is , which is equal to if is exactly a prime number, and equal to otherwise. That is, the number of prime numbers less than , plus half if equals a prime. Growth rate Of great interest in number theory is the growth rate of the prime-counting function. It was conjectured in the end of the 18th century by Gauss and by Legendre to be approximately \frac where is the natural logarithm, in the sense that \lim_ \frac=1. This statement is the prime number theorem. An equivalent statement is \lim_\frac=1 where is the logarithmic integral function. The prime number theorem was first proved in 1896 by Jacques Hadamard and by Charles de la Vallée Poussin independently, using properties of the Riemann zeta function introduced by Riemann in 1859. Proof ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Association Of America
The Mathematical Association of America (MAA) is a professional society that focuses on mathematics accessible at the undergraduate level. Members include university A university () is an educational institution, institution of tertiary education and research which awards academic degrees in several Discipline (academia), academic disciplines. ''University'' is derived from the Latin phrase , which roughly ..., college, and high school teachers; graduate and undergraduate students; pure and applied mathematicians; computer scientists; statisticians; and many others in academia, government, business, and industry. The MAA was founded in 1915 and is headquartered at 11 Dupont in the Dupont Circle, Washington, D.C., Dupont Circle neighborhood of Washington, D.C. The organization publishes mathematics journals and books, including the ''American Mathematical Monthly'' (established in 1894 by Benjamin Finkel), the most widely read mathematics journal in the world according to re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Oxford University Press
Oxford University Press (OUP) is the publishing house of the University of Oxford. It is the largest university press in the world. Its first book was printed in Oxford in 1478, with the Press officially granted the legal right to print books by decree in 1586. It is the second-oldest university press after Cambridge University Press, which was founded in 1534. It is a department of the University of Oxford. It is governed by a group of 15 academics, the Delegates of the Press, appointed by the Vice Chancellor, vice-chancellor of the University of Oxford. The Delegates of the Press are led by the Secretary to the Delegates, who serves as OUP's chief executive and as its major representative on other university bodies. Oxford University Press has had a similar governance structure since the 17th century. The press is located on Walton Street, Oxford, Walton Street, Oxford, opposite Somerville College, Oxford, Somerville College, in the inner suburb of Jericho, Oxford, Jericho. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dover Publications
Dover Publications, also known as Dover Books, is an American book publisher founded in 1941 by Hayward and Blanche Cirker. It primarily reissues books that are out of print from their original publishers. These are often, but not always, books in the public domain. The original published editions may be scarce or historically significant. Dover republishes these books, making them available at a significantly reduced cost. Classic reprints Dover reprints classic works of literature, classical sheet music, and public-domain images from the 18th and 19th centuries. Dover also publishes an extensive collection of mathematical, scientific, and engineering texts. It often targets its reprints at a niche market, such as woodworking. Starting in 2015, the company branched out into graphic novel reprints, overseen by Dover acquisitions editor and former comics writer and editor Drew Ford. Most Dover reprints are photo facsimiles of the originals, retaining the original pagination ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sieve Theory
Sieve theory is a set of general techniques in number theory, designed to count, or more realistically to estimate the size of, sifted sets of integers. The prototypical example of a sifted set is the set of prime numbers up to some prescribed limit ''X''. Correspondingly, the prototypical example of a sieve is the sieve of Eratosthenes, or the more general Legendre sieve. The direct attack on prime numbers using these methods soon reaches apparently insuperable obstacles, in the way of the accumulation of error terms. In one of the major strands of number theory in the twentieth century, ways were found of avoiding some of the difficulties of a frontal attack with a naive idea of what sieving should be. One successful approach is to approximate a specific sifted set of numbers (e.g. the set of prime numbers) by another, simpler set (e.g. the set of almost prime numbers), which is typically somewhat larger than the original set, and easier to analyze. More sophisticated sieves a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sieve Of Atkin
In mathematics, the sieve of Atkin is a modern algorithm for finding all prime numbers up to a specified integer. Compared with the ancient sieve of Eratosthenes, which marks off multiples of primes, the sieve of Atkin does some preliminary work and then marks off multiples of ''squares'' of primes, thus achieving a better theoretical asymptotic complexity. It was created in 2003 by A. O. L. Atkin and Daniel J. Bernstein.A.O.L. Atkin, D.J. Bernstein''Prime sieves using binary quadratic forms'' Math. Comp. 73 (2004), 1023-103/ref> Algorithm In the algorithm: *All remainders are Modulo operation, modulo-sixty remainders (divide the number by 60 and return the remainder). * All numbers, including and , are positive integers. * Flipping an entry in the sieve list means to change the marking (prime or nonprime) to the opposite marking. * This results in numbers with an odd number of solutions to the corresponding equation being potentially prime (prime if they are also square fre ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sieve Of Eratosthenes
In mathematics, the sieve of Eratosthenes is an ancient algorithm for finding all prime numbers up to any given limit. It does so by iteratively marking as composite number, composite (i.e., not prime) the multiples of each prime, starting with the first prime number, 2. The multiples of a given prime are generated as a sequence of numbers starting from that prime, with arithmetic progression, constant difference between them that is equal to that prime.Horsley, Rev. Samuel, F. R. S., "' or, The Sieve of Eratosthenes. Being an account of his method of finding all the Prime Numbers,''Philosophical Transactions'' (1683–1775), Vol. 62. (1772), pp. 327–347 This is the sieve's key distinction from using trial division to sequentially test each candidate number for divisibility by each prime. Once all the multiples of each discovered prime have been marked as composites, the remaining unmarked numbers are primes. The earliest known reference to the sieve (, ''kóskinon Eratosthén ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Zero-based Numbering
Zero-based numbering is a way of numbering in which the initial element of a sequence is assigned the index 0, rather than the index 1 as is typical in everyday non-mathematical or non-programming circumstances. Under zero-based numbering, the initial element is sometimes termed the '' zeroth'' element, rather than the ''first'' element; ''zeroth'' is a coined word for the ordinal number zero. In some cases, an object or value that does not (originally) belong to a given sequence, but which could be naturally placed before its initial element, may be termed the zeroth element. There is no wide agreement regarding the correctness of using zero as an ordinal (nor regarding the use of the term ''zeroth''), as it creates ambiguity for all subsequent elements of the sequence when lacking context. Numbering sequences starting at 0 is quite common in mathematics notation, in particular in combinatorics, though programming languages for mathematics usually index from 1. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sieve Of Eratosthenes
In mathematics, the sieve of Eratosthenes is an ancient algorithm for finding all prime numbers up to any given limit. It does so by iteratively marking as composite number, composite (i.e., not prime) the multiples of each prime, starting with the first prime number, 2. The multiples of a given prime are generated as a sequence of numbers starting from that prime, with arithmetic progression, constant difference between them that is equal to that prime.Horsley, Rev. Samuel, F. R. S., "' or, The Sieve of Eratosthenes. Being an account of his method of finding all the Prime Numbers,''Philosophical Transactions'' (1683–1775), Vol. 62. (1772), pp. 327–347 This is the sieve's key distinction from using trial division to sequentially test each candidate number for divisibility by each prime. Once all the multiples of each discovered prime have been marked as composites, the remaining unmarked numbers are primes. The earliest known reference to the sieve (, ''kóskinon Eratosthén ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
If And Only If
In logic and related fields such as mathematics and philosophy, "if and only if" (often shortened as "iff") is paraphrased by the biconditional, a logical connective between statements. The biconditional is true in two cases, where either both statements are true or both are false. The connective is biconditional (a statement of material equivalence), and can be likened to the standard material conditional ("only if", equal to "if ... then") combined with its reverse ("if"); hence the name. The result is that the truth of either one of the connected statements requires the truth of the other (i.e. either both statements are true, or both are false), though it is controversial whether the connective thus defined is properly rendered by the English "if and only if"—with its pre-existing meaning. For example, ''P if and only if Q'' means that ''P'' is true whenever ''Q'' is true, and the only case in which ''P'' is true is if ''Q'' is also true, whereas in the case of ''P if Q ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sieve Of Sundaram Animated
A sieve (), fine mesh strainer, or sift is a tool used for separating wanted elements from unwanted material or for controlling the particle size distribution of a sample, using a screen such as a woven mesh or net or perforated sheet material. The word ''sift'' derives from ''sieve''. In cooking, a sifter is used to separate and break up clumps in dry ingredients such as flour, as well as to aerate and combine them. A strainer (see colander), meanwhile, is a form of sieve used to separate suspended solids from a liquid by filtration. Sieving Sieving is a simple technique for separating particles of different sizes. A sieve such as used for sifting flour has very small holes. Coarse particles are separated or broken up by grinding against one another and the screen openings. Depending upon the types of particles to be separated, sieves with different types of holes are used. Sieves are also used to separate stones from sand. Sieving plays an important role in food industr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |