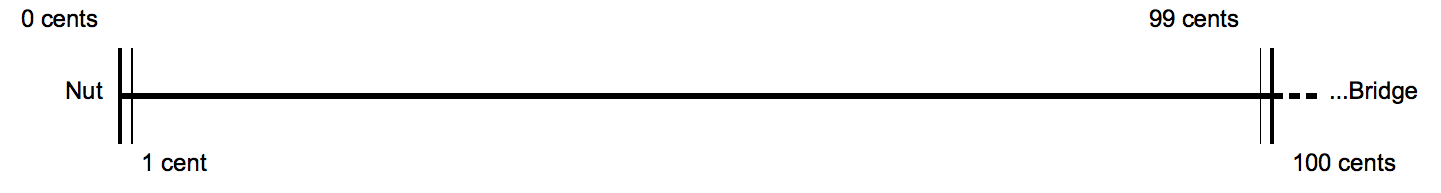|
Septimal Meantone
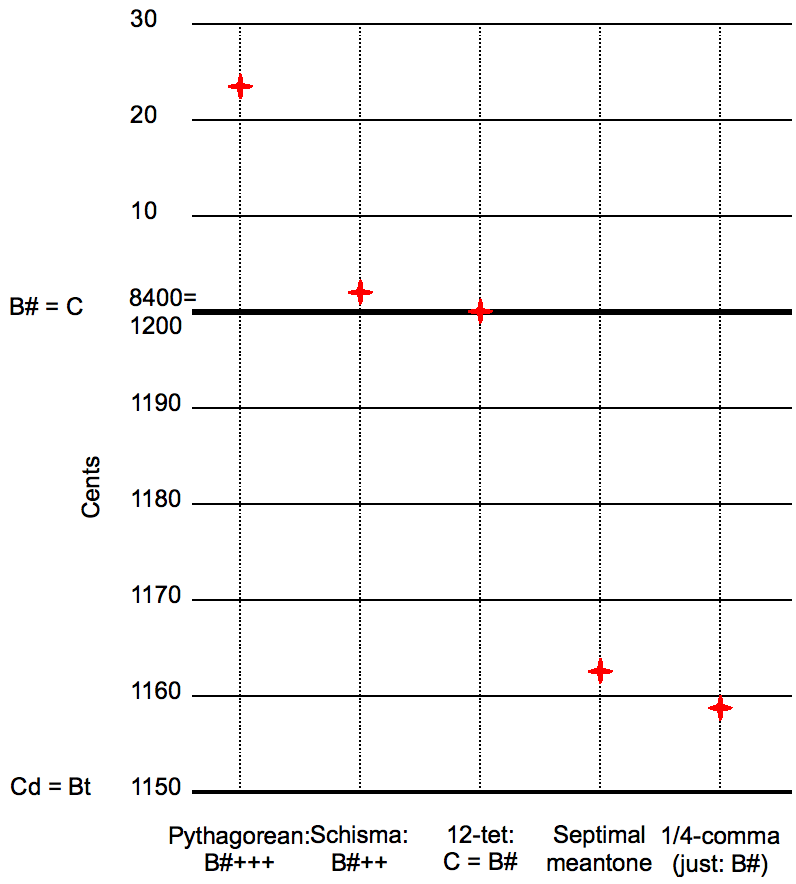
In music, septimal meantone temperament, also called ''standard septimal meantone'' or simply ''septimal meantone'', refers to the tempering of 7-limit musical intervals by a meantone temperament tuning in the range from fifths flattened by the amount of fifths for 12 equal temperament to those as flat as 19 equal temperament, with 31 equal temperament being a more or less optimal tuning for both the 5- and 7-limits. Choice of temperament Meantone temperament produces a frequency ratio of approximately 5 by means of four fifths, so that the major third (for instance C–E) is obtained from two successive whole tones. Septimal meantone produces the frequency ratio of 56 by ten fifths, so that the interval 7:4 is reached by five successive tones. Hence C–A, not C–B, represents a 7:4 interval in septimal meantone. : There are several slightly adjusted meantone tunings very nearly equivalent to exact quarter comma meantone, which all have good renditions of harmonic sevent ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Musical Temperament
In musical tuning, a temperament is a tuning system that slightly compromises the pure intervals of just intonation to meet other requirements. Most modern Western musical instruments are tuned in the equal temperament system. Tempering is the process of altering the size of an interval by making it narrower or wider than pure. "Any plan that describes the adjustments to the sizes of some or all of the twelve fifth intervals in the circle of fifths so that they accommodate pure octaves and produce certain sizes of major thirds is called a ''temperament''." Temperament is especially important for keyboard instruments, which typically allow a player to play only the pitches assigned to the various keys, and lack any way to alter pitch of a note in performance. Historically, the use of just intonation, Pythagorean tuning and meantone temperament meant that such instruments could sound "in tune" in one key, or some keys, but would then have more dissonance in other keys. In the w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cent (music)
The cent is a logarithmic unit of measure used for musical intervals. Twelve-tone equal temperament divides the octave into 12 semitones of 100 cents each. Typically, cents are used to express small intervals, to check intonation, or to compare the sizes of comparable intervals in different tuning systems. For humans, a single cent is too small to be perceived between successive notes. Cents, as described by Alexander John Ellis, follow a tradition of measuring intervals by logarithms that began with Juan Caramuel y Lobkowitz in the 17th century. Ellis chose to base his measures on the hundredth part of a semitone, \sqrt 200/math>, at Robert Holford Macdowell Bosanquet's suggestion. Making extensive measurements of musical instruments from around the world, Ellis used cents to report and compare the scales employed, and further described and utilized the system in his 1875 edition of Hermann von Helmholtz's ''On the Sensations of Tone''. It has become the standard me ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
50 Equal Temperament
5 (five) is a number, numeral and digit. It is the natural number, and cardinal number, following 4 and preceding 6, and is a prime number. Humans, and many other animals, have 5 digits on their limbs. Mathematics 5 is a Fermat prime, a Mersenne prime exponent, as well as a Fibonacci number. 5 is the first congruent number, as well as the length of the hypotenuse of the smallest integer-sided right triangle, making part of the smallest Pythagorean triple ( 3, 4, 5). 5 is the first safe prime and the first good prime. 11 forms the first pair of sexy primes with 5. 5 is the second Fermat prime, of a total of five known Fermat primes. 5 is also the first of three known Wilson primes (5, 13, 563). Geometry A shape with five sides is called a pentagon. The pentagon is the first regular polygon that does not tile the plane with copies of itself. It is the largest face any of the five regular three-dimensional regular Platonic solid can have. A conic is determined ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tristan Chord
The original Tristan chord is heard in the opening phrase of Richard Wagner's opera ''Tristan und Isolde'' as part of the leitmotif relating to Tristan. It is made up of the notes F, B, D, and G: : More generally, the term refers to any chord that consists of the same intervals: augmented fourth, augmented sixth, and augmented ninth above a bass note. Background The notes of the Tristan chord are not unusual; they could be respelled enharmonically to form a common half-diminished seventh chord. What distinguishes the Tristan chord is its unusual relationship to the implied key of its surroundings. : : This motif also appears in measures 6, 10, and 12, several times later in the work, and at the end of the last act. points out the "chord" in earlier works by Guillaume de Machaut, Carlo Gesualdo, J. S. Bach, Mozart, Beethoven, or Louis Spohr as in the following example from the first movement of Beethoven's Piano Sonata No. 18: : : The chord is found ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Augmented Sixth Chord
In music theory, an augmented sixth chord contains the interval (music), interval of an augmented sixth, usually above its bass note, bass tone. This chord (music), chord has its origins in the Renaissance music, Renaissance, was further developed in the Baroque music, Baroque, and became a distinctive part of the musical style of the Classical period (music), Classical and Romantic period (music), Romantic periods. Conventionally used with a predominant chord, predominant diatonic function, function (resolution (music), resolving to the dominant (music), dominant), the three most common types of augmented sixth chords are usually called the ''Italian sixth'', the ''French sixth'', and the ''German sixth''. Augmented sixth interval The augmented sixth interval is typically between the sixth scale degree, degree of the Major and minor, minor scale, , and the raised fourth degree, . With standard voice leading, the chord is followed directly or indirectly by some form of the do ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Common Practice Period
In Western classical music, the common practice period (CPP) was the period of about 250 years during which the tonal system was regarded as the only basis for composition. It began when composers' use of the tonal system had clearly superseded earlier systems, and ended when some composers began using significantly modified versions of the tonal system, and began developing other systems as well. Most features of common practice (the accepted concepts of composition during this time) persisted from the mid-Baroque period through the Classical and Romantic periods, roughly from 1650 to 1900. There was much stylistic evolution during these centuries, with patterns and conventions flourishing and then declining, such as the sonata form. The most prominent unifying feature throughout the period is a harmonic language to which music theorists can today apply Roman numeral chord analysis; however, the "common" in common practice does not directly refer to any type of harmony, rat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Utonal
''Otonality'' and ''utonality'' are terms introduced by Harry Partch to describe chords whose pitch classes are the harmonics or subharmonics of a given fixed tone (identity), respectively. For example: , , ,... or , , ,.... Definition An otonality is a collection of pitches which can be expressed in ratios, expressing their relationship to the fixed tone, that have equal denominators and consecutive numerators. For example, , , and ( just major chord) form an otonality because they can be written as , , . This in turn can be written as an extended ratio 4:5:6. Every otonality is therefore composed of members of a harmonic series. Similarly, the ratios of a utonality share the same numerator and have consecutive denominators. , , , and () form a utonality, sometimes written as , or as . Every utonality is therefore composed of members of a subharmonic series. This term is used extensively by Harry Partch in ''Genesis of a Music''. An otonality corresponds to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Septimal Kleisma
In music, the ratio 225/224 is called the septimal kleisma (). It is a minute comma type interval of approximately 7.7 cents. Factoring it into primes gives 2−5 32 52 7−1, which can be rewritten 2−1 (5/4)2 (9/7). That says that it is the amount that two major thirds of 5/4 and a septimal major third, or supermajor third, of 9/7 exceeds the octave. The septimal kleisma can also be viewed as the difference between the diatonic semitone A semitone, also called a minor second, half step, or a half tone, is the smallest interval (music), musical interval commonly used in Western tonal music, and it is considered the most Consonance and dissonance#Dissonance, dissonant when sounde ... (16:15) and the septimal diatonic semitone (15:14). References 7-limit tuning and intervals Commas (music) 0225:0224 {{music-theory-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Septimal Semicomma
In music, the septimal semicomma, a seven- limit semicomma, is the ratio 126/125 and is equal to approximately 13.79 cents (). It is also called the ''small septimal comma''Haluska, Jan (2003). ''The Mathematical Theory of Tone Systems'', p.xxvi. . and the ''starling comma'' after its use in starling temperament. Factored into primes it is: 2*3^2*5^*7 Or as simple just intervals: (6/5)^3*(7/6)*(2/1)^ Thus it is the difference between three minor thirds of 6/5 plus a septimal minor third of 7/6 and an octave (2/1). This comma is important to certain tuning systems, such as septimal meantone temperament. A diminished seventh chord consisting of three minor thirds and a subminor third making up an octave is possible in such systems. This characteristic feature of these tuning systems is known as the ''septimal semicomma diminished seventh chord''. In equal temperament It is tempered out in 19 equal temperament and 31 equal temperament, but not in 22 equal temperament, 34 equa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Syntonic Comma
In music theory Music theory is the study of theoretical frameworks for understanding the practices and possibilities of music. ''The Oxford Companion to Music'' describes three interrelated uses of the term "music theory": The first is the "Elements of music, ..., the syntonic comma, also known as the chromatic diesis, the Didymean comma, the Ptolemy, Ptolemaic comma, or the diatonic comma is a small Comma (music), comma type interval (music), interval between two musical notes, equal to the frequency ratio (= 1.0125) (around 21.51 cent (music), cents). Two notes that differ by this interval would sound different from each other even to untrained ears, but would be close enough that they would be more likely interpreted as out-of-tune versions of the same note than as different notes. The comma is also referred to as a ''Didymean comma'' because it is the amount by which Didymus the Musician, Didymus corrected the Pythagorean interval, Pythagorean major thir ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quarter-comma Meantone
Quarter-comma meantone, or -comma meantone, was the most common meantone temperament in the sixteenth and seventeenth centuries, and was sometimes used later. In this system the perfect fifth is flattened by one quarter of a syntonic comma with respect to its just intonation used in Pythagorean tuning ( frequency ratio the result is \tfrac \times \left(\tfrac\right)^ = \sqrt \approx 1.49535, or a fifth of 696.578 cents. (The 12th power of that value is 125, whereas 7 octaves is 128, and so falls 41.059 cents short.) This fifth is then iterated to generate the diatonic scale and other notes of the temperament. The purpose is to obtain justly intoned major thirds (with a frequency ratio equal to It was described by Pietro Aron in his ''Toscanello de la Musica'' of 1523, by saying the major thirds should be tuned to be "sonorous and just, as united as possible". Later theorists Gioseffo Zarlino and Francisco de Salinas described the tuning with mathematical ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |