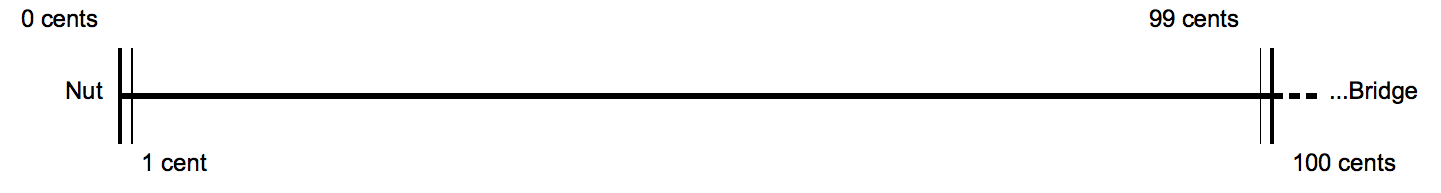|
Savart
The savart is a unit of measurement for musical pitch intervals (). One savart is equal to one thousandth of a decade ( 10/1: 3,986.313714 cents): 3.9863 cents. Musically, in just intonation, the interval of a decade is precisely a just major twenty-fourth, or, in other words, three octaves and a just major third. Today the savart has largely been replaced by the cent and the millioctave. The savart is practically the same as the earlier heptameride (eptameride), one seventh of a meride (). One tenth of an heptameride is a decameride () and a hundredth of an heptameride (thousandth of a decade) is approximately one jot (). Definition If \frac is the ratio of frequencies of a given interval, the corresponding measure in savarts is given by: s = 1000 \log_ or \frac = 10^ Like the more common cent, the savart is a logarithmic measure, and thus intervals can be added by simply adding their savart values, instead of multiplying them as you would frequencies. The number of sav ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Félix Savart
Félix Savart (; ; 30 June 1791, Mézières – 16 March 1841, Paris) was a French physicist and mathematician who is primarily known for the Biot–Savart law of electromagnetism, which he discovered together with his colleague Jean-Baptiste Biot. His main interest was in acoustics and the study of vibrating bodies. A particular interest in the violin led him to create an experimental trapezoidal model. He gave his name to the savart, a unit of measurement for musical intervals, and to Savart's wheel—a device he used while investigating the range of human hearing. Biography Savart was the son of Gérard Savart, an engineer at the military school of Metz. His brother, Nicolas, who was a student at the École Polytechnique and an officer in the engineering corps, did work on vibration. At the military hospital at Metz, Savart studied medicine and later went on to the University of Strasbourg, where he received his medical degree in 1816. Savart became a professor at C ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cent (music)
The cent is a logarithmic unit of measure used for musical intervals. Twelve-tone equal temperament divides the octave into 12 semitones of 100 cents each. Typically, cents are used to express small intervals, or to compare the sizes of comparable intervals in different tuning systems, and in fact the interval of one cent is too small to be perceived between successive notes. Cents, as described by Alexander John Ellis, follow a tradition of measuring intervals by logarithms that began with Juan Caramuel y Lobkowitz in the 17th century. Ellis chose to base his measures on the hundredth part of a semitone, , at Robert Holford Macdowell Bosanquet's suggestion. He made extensive measurements of musical instruments from around the world, using cents extensively to report and compare the scales employed, and further described and employed the system in his 1875 edition of Hermann von Helmholtz's ''On the Sensations of Tone''. It has become the standard method of representi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
List Of Pitch Intervals
Below is a list of intervals expressible in terms of a prime limit (see Terminology), completed by a choice of intervals in various equal subdivisions of the octave or of other intervals. For commonly encountered harmonic or melodic intervals between pairs of notes in contemporary Western music theory, without consideration of the way in which they are tuned, see . Terminology *The ''prime limit'' Fox, Christopher (2003). "Microtones and Microtonalities", ''Contemporary Music Review'', v. 22, pt. 1–2. (Abingdon, Oxfordshire, UK: Routledge): p. 13. henceforth referred to simply as the ''limit'', is the largest prime number occurring in the factorizations of the numerator and denominator of the frequency ratio describing a rational interval. For instance, the limit of the just perfect fourth (4:3) is 3, but the just minor tone (10:9) has a limit of 5, because 10 can be factored into (and 9 into ). There exists another type of limit, the '' odd limit'', a concept used by Harry ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Decade (log Scale)
One decade (symbol dec) is a unit for measuring ratios on a logarithmic scale, with one decade corresponding to a ratio of 10 between two numbers. Example: Scientific notation When a real number like .007 is denoted alternatively by 7. × 10—3 then it is said that the number is represented in scientific notation. More generally, to write a number in the form ''a'' × 10''b'', where 1 < ''a'' < 10 and ''b'' is an , is to express it in , and ''a'' is called the ''significand'' or the ''mantissa'', and ''b'' is its |
Millioctave
The millioctave (moct) is a unit of measurement for musical intervals. As is expected from the prefix milli-, a millioctave is defined as 1/1000 of an octave. From this it follows that one millioctave is equal to the ratio 21/1000, the 1000th root of 2, or approximately 1.0006934 (). Given two frequencies ''a'' and ''b'', the measurement of the interval between them in millioctaves can be calculated by :n = 1000 \log_2 \left( \frac \right) \approx 3322 \log_ \left( \frac \right) Likewise, if you know a note ''b'' and the number ''n'' of millioctaves in the interval, then the other note ''a'' may be calculated by: :a = b \times 2 ^ \frac Like the more common cent, the millioctave is a linear measure of intervals, and thus the size of intervals can be calculated by adding their millioctave values, instead of multiplication, which is necessary for calculations of frequencies. A millioctave is exactly 1.2 cents. History and use The millioctave was introduced by the German physic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Intervals (music)
In music theory, an interval is a difference in pitch between two sounds. An interval may be described as horizontal, linear, or melodic if it refers to successively sounding tones, such as two adjacent pitches in a melody, and vertical or harmonic if it pertains to simultaneously sounding tones, such as in a chord. In Western music, intervals are most commonly differences between notes of a diatonic scale. Intervals between successive notes of a scale are also known as scale steps. The smallest of these intervals is a semitone. Intervals smaller than a semitone are called microtones. They can be formed using the notes of various kinds of non-diatonic scales. Some of the very smallest ones are called commas, and describe small discrepancies, observed in some tuning systems, between enharmonically equivalent notes such as C and D. Intervals can be arbitrarily small, and even imperceptible to the human ear. In physical terms, an interval is the ratio between two sonic frequen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Equal Temperaments
Equal(s) may refer to: Mathematics * Equality (mathematics). * Equals sign (=), a mathematical symbol used to indicate equality. Arts and entertainment * ''Equals'' (film), a 2015 American science fiction film * ''Equals'' (game), a board game * The Equals, a British pop group formed in 1965 * "Equal", a 2016 song by Chrisette Michele from ''Milestone'' * "Equal", a 2022 song by Odesza featuring Låpsley from '' The Last Goodbye'' * "Equals", a 2009 song by Set Your Goals from ''This Will Be the Death of Us'' * ''Equal'' (TV series), a 2020 American docuseries on HBO * ''='' (album), a 2021 album by Ed Sheeran * "=", a 2022 song by J-Hope from ''Jack in the Box'' Other uses * Equal (sweetener) Equal is an American brand of artificial sweetener containing aspartame, acesulfame potassium, dextrose and maltodextrin. It is marketed as a tabletop sweetener by Merisant, a global corporation which also used to own the well-known NutraSweet ..., a brand of artificial sweetener. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Musical Tuning
In music, there are two common meanings for tuning: * Tuning practice, the act of tuning an instrument or voice. * Tuning systems, the various systems of pitches used to tune an instrument, and their theoretical bases. Tuning practice Tuning is the process of adjusting the pitch of one or many tones from musical instruments to establish typical intervals between these tones. Tuning is usually based on a fixed reference, such as A = 440 Hz. The term "''out of tune''" refers to a pitch/tone that is either too high ( sharp) or too low ( flat) in relation to a given reference pitch. While an instrument might be in tune relative to its own range of notes, it may not be considered 'in tune' if it does not match the chosen reference pitch. Some instruments become 'out of tune' with temperature, humidity, damage, or simply time, and must be readjusted or repaired. Different methods of sound production require different methods of adjustment: * Tuning to a pitch with one's voi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Decidecade
A one-third octave is a logarithmic unit of frequency ratio equal to either one third of an octave (1200/3 = 400 cents: major third) or one tenth of a decade (3986.31/10 = 398.631 cents: M3 ). An alternative (unambiguous) term for one tenth of a decade is a decidecade. One octave is a factor of 2, so \log_ (2) = 0.301 decades per octave, while a third would be 0.\overline. Definitions Base 2 ISO 18405:2017 defines a "one-third octave" (or "one-third octave (base 2)") as one third of an octave, corresponding to a frequency ratio of 2^. A one-third octave (base 2) is precisely 400 cents. Base 10 IEC 61260-1:2014 and ANSI S1.6-2016 define a "one-third octave" as one tenth of a decade, corresponding to a frequency ratio of 10^. This unit is referred to by ISO 18405 as a "decidecade" or "one-third octave (base 10)".(This makes sense as, if we want one third of an octave, the ratio will be f2/f1=2^, and if we log10 both members of equation we have, log=log-> log(f2/f1)=log(2)*1/3, wh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hermann Von Helmholtz
Hermann Ludwig Ferdinand von Helmholtz (31 August 1821 – 8 September 1894) was a German physicist and physician who made significant contributions in several scientific fields, particularly hydrodynamic stability. The Helmholtz Association, the largest German association of research institutions, is named in his honor. In the fields of physiology and psychology, Helmholtz is known for his mathematics concerning the eye, theories of vision, ideas on the visual perception of space, color vision research, the sensation of tone, perceptions of sound, and empiricism in the physiology of perception. In physics, he is known for his theories on the conservation of energy, work in electrodynamics, chemical thermodynamics, and on a mechanical foundation of thermodynamics. As a philosopher, he is known for his philosophy of science, ideas on the relation between the laws of perception and the laws of nature, the science of aesthetics, and ideas on the civilizing power o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
John Curwen
John Curwen (14 November 1816 – 26 May 1880) was an English Congregationalist minister and diffuser of the tonic sol-fa system of music education created by Sarah Ann Glover. He was educated at Wymondley College in Hertfordshire, then Coward College as that institution became known when it moved to London, and finally University College London. Background and biography John Curwen was a descendant of the Curwens of Workington Hall in Cumbria, one of the oldest families in England, the male line proper being a direct descent from Eldred, a pre-Norman Englishman, whose son Ketel held lands in the Barony of Kendal. Orm, Ketel's son, inherited the Cumbrian manor of Workington. Curwen was born 14 November 1816, at Heckmondwike, West Riding of Yorkshire, the son of Spedding Curwen and Mary Jubb. His father was a Non-conformist minister, as John was also from 1838 until 1864. Curwen gave up full-time ministry to devote himself to his new method of musical nomenclature. He es ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |