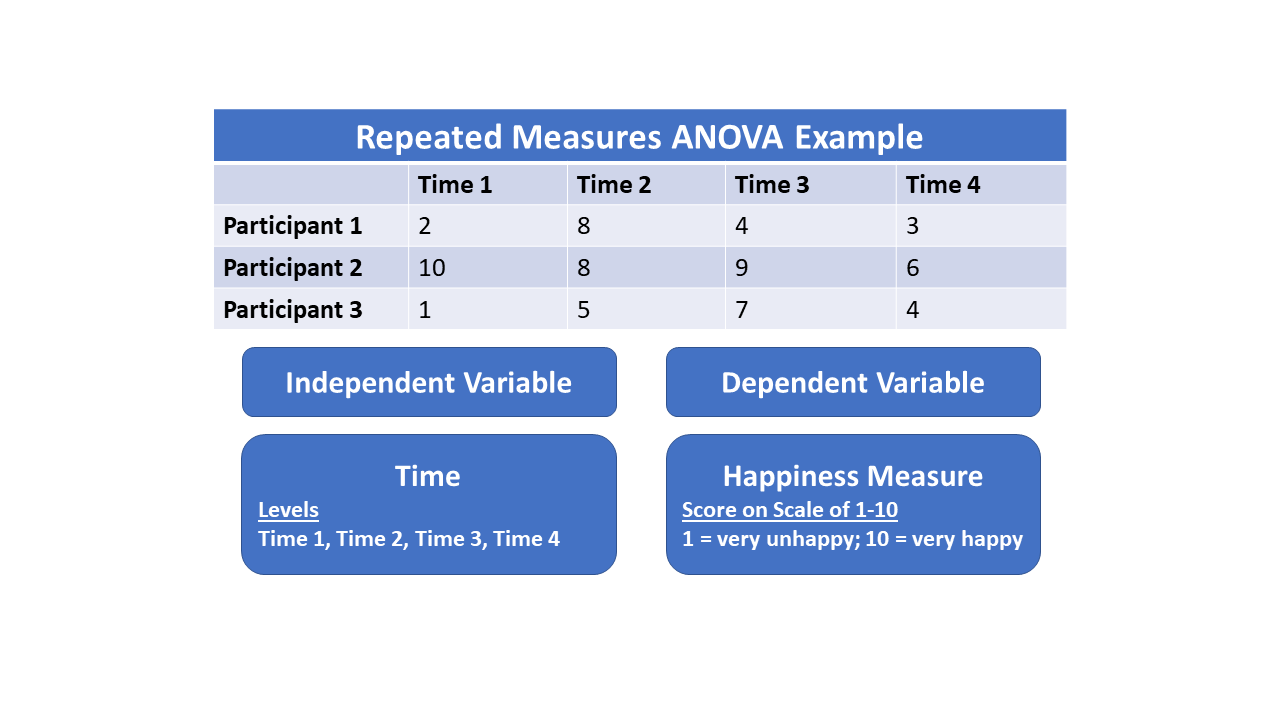
|
Repeated Measures
Repeated measures design is a research design that involves multiple measures of the same variable taken on the same or matched subjects either under different conditions or over two or more time periods. For instance, repeated measurements are collected in a longitudinal study in which change over time is assessed. Crossover studies A popular repeated-measures design is the crossover study. A crossover study is a longitudinal study in which subjects receive a sequence of different treatments (or exposures). While crossover studies can be observational studies, many important crossover studies are controlled experiments. Crossover designs are common for experiments in many scientific disciplines, for example psychology, education, pharmaceutical science, and health care, especially medicine. Randomized, controlled, crossover experiments are especially important in health care. In a randomized clinical trial, the subjects are randomly assigned treatments. When such a trial is a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Research Design
Research design refers to the overall strategy utilized to carry out research that defines a succinct and logical plan to tackle established research question(s) through the collection, interpretation, analysis, and discussion of data. Incorporated in the design of a research study will depend on the standpoint of the researcher over their beliefs in the nature of knowledge (see epistemology) and reality (see ontology), often shaped by the disciplinary areas the researcher belongs to. The design of a study defines the study type (descriptive, correlational, semi-experimental, experimental, review, meta-analytic) and sub-type (e.g., descriptive-longitudinal case study), research problem, hypotheses, independent and dependent variables, experimental design, and, if applicable, data collection methods and a statistical analysis plan. A research design is a framework that has been created to find answers to research questions. Design types and sub-types There are many ways to cl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Order Effect
Order, ORDER or Orders may refer to: * Categorization, the process in which ideas and objects are recognized, differentiated, and understood * Heterarchy, a system of organization wherein the elements have the potential to be ranked a number of different ways * Hierarchy, an arrangement of items that are represented as being "above", "below", or "at the same level as" one another * an action or inaction that must be obeyed, mandated by someone in authority People * Orders (surname) Arts, entertainment, and media * ''Order'' (album), a 2009 album by Maroon * "Order", a 2016 song from '' Brand New Maid'' by Band-Maid * ''Orders'' (1974 film), a 1974 film by Michel Brault * ''Orders'', a 2010 film by Brian Christopher * ''Orders'', a 2017 film by Eric Marsh and Andrew Stasiulis * ''Jed & Order'', a 2022 film by Jedman Business * Blanket order, purchase order to allow multiple delivery dates over a period of time * Money order or postal order, a financial instrument usually int ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Clinical Trial Protocol
In natural and social science research, a protocol is most commonly a predefined procedural method in the design and implementation of an experiment. Protocols are written whenever it is desirable to standardize a laboratory method to ensure successful replication of results by others in the same laboratory or by other laboratories. Additionally, and by extension, protocols have the advantage of facilitating the assessment of experimental results through peer review. In addition to detailed procedures, equipment, and instruments, protocols will also contain study objectives, reasoning for experimental design, reasoning for chosen sample sizes, safety precautions, and how results were calculated and reported, including statistical analysis and any rules for predefining and documenting excluded data to avoid bias. Similarly, a protocol may refer to the procedural methods of health organizations, commercial laboratories, manufacturing plants, etc. to ensure their activities (e.g., blo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Analysis Of Variance
Analysis of variance (ANOVA) is a collection of statistical models and their associated estimation procedures (such as the "variation" among and between groups) used to analyze the differences among means. ANOVA was developed by the statistician Ronald Fisher. ANOVA is based on the law of total variance, where the observed variance in a particular variable is partitioned into components attributable to different sources of variation. In its simplest form, ANOVA provides a statistical test of whether two or more population means are equal, and therefore generalizes the ''t''-test beyond two means. In other words, the ANOVA is used to test the difference between two or more means. History While the analysis of variance reached fruition in the 20th century, antecedents extend centuries into the past according to Stigler. These include hypothesis testing, the partitioning of sums of squares, experimental techniques and the additive model. Laplace was performing hypothesis testi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mixed Model
A mixed model, mixed-effects model or mixed error-component model is a statistical model containing both fixed effects and random effects. These models are useful in a wide variety of disciplines in the physical, biological and social sciences. They are particularly useful in settings where repeated measurements are made on the same statistical units (longitudinal study), or where measurements are made on clusters of related statistical units. Because of their advantage in dealing with missing values, mixed effects models are often preferred over more traditional approaches such as repeated measures analysis of variance. This page will discuss mainly linear mixed-effects models (LMEM) rather than generalized linear mixed models or nonlinear mixed-effects models. History and current status Ronald Fisher introduced random effects models to study the correlations of trait values between relatives. In the 1950s, Charles Roy Henderson provided best linear unbiased estimates ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Effect Size
In statistics, an effect size is a value measuring the strength of the relationship between two variables in a population, or a sample-based estimate of that quantity. It can refer to the value of a statistic calculated from a sample of data, the value of a parameter for a hypothetical population, or to the equation that operationalizes how statistics or parameters lead to the effect size value. Examples of effect sizes include the correlation between two variables, the regression coefficient in a regression, the mean difference, or the risk of a particular event (such as a heart attack) happening. Effect sizes complement statistical hypothesis testing, and play an important role in power analyses, sample size planning, and in meta-analyses. The cluster of data-analysis methods concerning effect sizes is referred to as estimation statistics. Effect size is an essential component when evaluating the strength of a statistical claim, and it is the first item (magnitude) in the MA ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Greenhouse–Geisser Correction
The Greenhouse–Geisser correction \widehat is a statistical method of adjusting for lack of sphericity in a repeated measures ANOVA. The correction functions as both an estimate of epsilon (sphericity) and a correction for lack of sphericity. The correction was proposed by Samuel Greenhouse and Seymour Geisser in 1959. The Greenhouse–Geisser correction is an estimate of sphericity (\widehat). If sphericity is met, then \varepsilon = 1 . If sphericity is not met, then epsilon will be less than 1 (and the degrees of freedom will be overestimated and the F-value will be inflated). To correct for this inflation, multiply the Greenhouse–Geisser estimate of epsilon to the degrees of freedom used to calculate the F critical value. An alternative correction that is believed to be less conservative is the Huynh–Feldt correction (1976). As a general rule of thumb, the Greenhouse–Geisser correction is the preferred correction method when the epsilon estimate is below 0.75. Otherwi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
F Statistic
An ''F''-test is any statistical test in which the test statistic has an ''F''-distribution under the null hypothesis. It is most often used when comparing statistical models that have been fitted to a data set, in order to identify the model that best fits the population from which the data were sampled. Exact "''F''-tests" mainly arise when the models have been fitted to the data using least squares. The name was coined by George W. Snedecor, in honour of Ronald Fisher. Fisher initially developed the statistic as the variance ratio in the 1920s. Common examples Common examples of the use of ''F''-tests include the study of the following cases: * The hypothesis that the means of a given set of normally distributed populations, all having the same standard deviation, are equal. This is perhaps the best-known ''F''-test, and plays an important role in the analysis of variance (ANOVA). * The hypothesis that a proposed regression model fits the data well. See Lack-of- ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mauchly's Sphericity Test
Mauchly's sphericity test or Mauchly's ''W'' is a statistical test used to validate a repeated measures analysis of variance (ANOVA). It was developed in 1940 by John Mauchly. Sphericity Sphericity is an important assumption of a repeated-measures ANOVA. It is the condition of equal variances among the differences between all possible pairs of within-subject conditions (i.e., levels of the independent variable). If sphericity is violated (i.e., if the variances of the differences between all combinations of the conditions are not equal), then the variance calculations may be distorted, which would result in an inflated F-ratio. Sphericity can be evaluated when there are three or more levels of a repeated measure factor and, with each additional repeated measures factor, the risk for violating sphericity increases. If sphericity is violated, a decision must be made as to whether a univariate or multivariate analysis is selected. If a univariate method is selected, the repeated-mea ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Normal Distribution
In statistics, a normal distribution or Gaussian distribution is a type of continuous probability distribution for a real-valued random variable. The general form of its probability density function is : f(x) = \frac e^ The parameter \mu is the mean or expectation of the distribution (and also its median and mode), while the parameter \sigma is its standard deviation. The variance of the distribution is \sigma^2. A random variable with a Gaussian distribution is said to be normally distributed, and is called a normal deviate. Normal distributions are important in statistics and are often used in the natural and social sciences to represent real-valued random variables whose distributions are not known. Their importance is partly due to the central limit theorem. It states that, under some conditions, the average of many samples (observations) of a random variable with finite mean and variance is itself a random variable—whose distribution converges to a normal dist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Type 1 Error
In statistical hypothesis testing, a type I error is the mistaken rejection of an actually true null hypothesis (also known as a "false positive" finding or conclusion; example: "an innocent person is convicted"), while a type II error is the failure to reject a null hypothesis that is actually false (also known as a "false negative" finding or conclusion; example: "a guilty person is not convicted"). Much of statistical theory revolves around the minimization of one or both of these errors, though the complete elimination of either is a statistical impossibility if the outcome is not determined by a known, observable causal process. By selecting a low threshold (cut-off) value and modifying the alpha (α) level, the quality of the hypothesis test can be increased. The knowledge of type I errors and type II errors is widely used in medical science, biometrics and computer science. Intuitively, type I errors can be thought of as errors of ''commission'', i.e. the researcher unluck ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
F-test
An ''F''-test is any statistical test in which the test statistic has an ''F''-distribution under the null hypothesis. It is most often used when comparing statistical models that have been fitted to a data set, in order to identify the model that best fits the population from which the data were sampled. Exact "''F''-tests" mainly arise when the models have been fitted to the data using least squares. The name was coined by George W. Snedecor, in honour of Ronald Fisher. Fisher initially developed the statistic as the variance ratio in the 1920s. Common examples Common examples of the use of ''F''-tests include the study of the following cases: * The hypothesis that the means of a given set of normally distributed populations, all having the same standard deviation, are equal. This is perhaps the best-known ''F''-test, and plays an important role in the analysis of variance (ANOVA). * The hypothesis that a proposed regression model fits the data well. See Lack-of-f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
