|
Quasiperiodic
Quasiperiodicity is the property of a system that displays irregular periodicity. Periodic behavior is defined as recurring at regular intervals, such as "every 24 hours". Quasiperiodic behavior is almost but not quite periodic. The term used to denote oscillations that appear to follow a regular pattern but which do not have a fixed period. The term thus used does not have a precise definition and should not be confused with more strictly defined mathematical concepts such as an almost periodic function or a quasiperiodic function. Climatology Climate oscillations that appear to follow a regular pattern but which do not have a fixed period are called ''quasiperiodic''.''The meteorological glossary: 2d ed.'' 1930. Meteorological Office, Great Britain. "Certain phenomena which recur more or less regularly but without the exactness of truly periodic phenomena are termed quasi-periodic." Within a dynamical system such as the ocean-atmosphere system, oscillations may occur regularly ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quasiperiodic Motion
In mathematics and theoretical physics, quasiperiodic motion is motion on a torus that never comes back to the same point. This behavior can also be called quasiperiodic evolution, dynamics, or flow. The torus may be a generalized torus so that the neighborhood of any point is more than two-dimensional. At each point of the torus there is a direction of motion that remains on the torus. Once a flow on a torus is defined or fixed, it determines trajectories. If the trajectories come back to a given point after a certain time then the motion is periodic with that period, otherwise it is quasiperiodic. The quasiperiodic motion is characterized by a finite set of frequencies which can be thought of as the frequencies at which the motion goes around the torus in different directions. For instance, if the torus is the surface of a doughnut, then there is the frequency at which the motion goes around the doughnut and the frequency at which it goes inside and out. But the set of frequenci ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
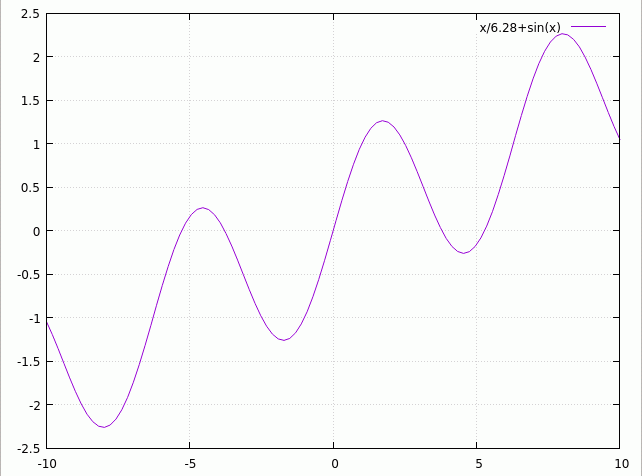
Quasiperiodic Function
In mathematics, a quasiperiodic function is a function that has a certain similarity to a periodic function. A function f is quasiperiodic with quasiperiod \omega if f(z + \omega) = g(z,f(z)), where g is a "''simpler''" function than f. What it means to be "''simpler''" is vague. A simple case (sometimes called arithmetic quasiperiodic) is if the function obeys the equation: :f(z + \omega) = f(z) + C Another case (sometimes called geometric quasiperiodic) is if the function obeys the equation: :f(z + \omega) = C f(z) An example of this is the Jacobi theta function, where :\vartheta(z+\tau;\tau) = e^\vartheta(z;\tau), shows that for fixed \tau it has quasiperiod \tau; it also is periodic with period one. Another example is provided by the Weierstrass sigma function, which is quasiperiodic in two independent quasiperiods, the periods of the corresponding Weierstrass ''℘'' function. Bloch's theorem says that the eigenfunctions of a periodic Schrödinger equation (or o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Almost Periodic Function
In mathematics, an almost periodic function is, loosely speaking, a function of a real variable that is periodic to within any desired level of accuracy, given suitably long, well-distributed "almost-periods". The concept was first studied by Harald Bohr and later generalized by Vyacheslav Stepanov, Hermann Weyl and Abram Samoilovitch Besicovitch, amongst others. There is also a notion of almost periodic functions on locally compact abelian groups, first studied by John von Neumann. Almost periodicity is a property of dynamical systems that appear to retrace their paths through phase space, but not exactly. An example would be a planetary system, with planets in orbits moving with periods that are not commensurable (i.e., with a period vector that is not proportional to a vector of integers). A theorem of Kronecker from diophantine approximation can be used to show that any particular configuration that occurs once, will recur to within any specified accuracy: if we wai ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Climate Oscillation
Climate variability includes all the variations in the climate that last longer than individual weather events, whereas the term climate change only refers to those variations that persist for a longer period of time, typically decades or more. ''Climate change'' may refer to any time in Earth's history, but the term is now commonly used to describe contemporary climate change, often popularly referred to as global warming. Since the Industrial Revolution, the climate has increasingly been affected by human activities. The climate system receives nearly all of its energy from the sun and radiates energy to outer space. The balance of incoming and outgoing energy and the passage of the energy through the climate system is Earth's energy budget. When the incoming energy is greater than the outgoing energy, Earth's energy budget is positive and the climate system is warming. If more energy goes out, the energy budget is negative and Earth experiences cooling. The energy moving t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Seasonality
In time series data, seasonality refers to the trends that occur at specific regular intervals less than a year, such as weekly, monthly, or quarterly. Seasonality may be caused by various factors, such as weather, vacation, and holidays and consists of periodic, repetitive, and generally regular and predictable patterns in the levels of a time series. Seasonal fluctuations in a time series can be contrasted with cyclical patterns. The latter occur when the data exhibits rises and falls that are not of a fixed period. Such non-seasonal fluctuations are usually due to economic conditions and are often related to the "business cycle"; their period usually extends beyond a single year, and the fluctuations are usually of at least two years. Organisations facing seasonal variations, such as ice-cream vendors, are often interested in knowing their performance relative to the normal seasonal variation. Seasonal variations in the labour market can be attributed to the entrance of school ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quasiperiodic Tiling
A quasiperiodic tiling is a tiling of the plane that exhibits local periodicity under some transformations: every finite subset of its tiles reappears infinitely often throughout the tiling, but there is no nontrivial way of superimposing the whole tiling onto itself so that all tiles overlap perfectly. See also * Aperiodic tiling and Penrose tiling for a mathematical viewpoint * Quasicrystal A quasiperiodicity, quasiperiodic crystal, or quasicrystal, is a structure that is Order and disorder (physics), ordered but not Bravais lattice, periodic. A quasicrystalline pattern can continuously fill all available space, but it lacks trans ... for a physics viewpoint References {{Reflist Tessellation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
System
A system is a group of interacting or interrelated elements that act according to a set of rules to form a unified whole. A system, surrounded and influenced by its open system (systems theory), environment, is described by its boundaries, structure and purpose and is expressed in its functioning. Systems are the subjects of study of systems theory and other systems sciences. Systems have several common properties and characteristics, including structure, function(s), behavior and interconnectivity. Etymology The term ''system'' comes from the Latin word ''systēma'', in turn from Greek language, Greek ''systēma'': "whole concept made of several parts or members, system", literary "composition"."σύστημα" , Henry George Liddell, Robert Scott, ''A Greek–English Lexicon'', on Pers ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Climate (journal)
This is a list of academic journals published by MDPI. As of September 2022, MDPI publishes 399 peer-reviewed academic journals and nine conference journals. {, class="wikitable sortable" , +List of MDPI journals !Journal name !Subject !Established !ISSN , - , ''Acoustics'' , Engineering , 2019 , 2624-599X , - , ''Actuators'' , Engineering , 2012 , 2076-0825 , - , ''Administrative Sciences'' , Business , 2011 , 2076-3387 , - , ''Adolescents'' , Health , 2021 , 2673-7051 , - , ''Advances in Respiratory Medicine'' (formerly ''Pneumonologia i Alergologia Polska)'' , Health , , 2451-4934 , - , ''Aerospace'' , Engineering , 2014 , 2226-4310 , - , ''Agriculture'' , Agriculture , 2011 , 2077-0472 , - , ''AgriEngineering'' , Agriculture , 2019 , 2624-7402 , - , ''Agronomy'' , Agriculture , 2011 , 2073-4395 , - , ''AI'' , Computers , 2020 , 2673-2688 , - , ''Algorithms'' , Mathematics , 2008 , 1999-4893 , - , ''Allergies'' , Medicine , 2021 , 2313-5786 , - , ''Alloys'' , Engineering ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Systems Theory
Systems theory is the Transdisciplinarity, transdisciplinary study of systems, i.e. cohesive groups of interrelated, interdependent components that can be natural or artificial. Every system has causal boundaries, is influenced by its context, defined by its structure, function and role, and expressed through its relations with other systems. A system is "more than the sum of its parts" when it expresses synergy or emergent behavior. Changing one component of a system may affect other components or the whole system. It may be possible to predict these changes in patterns of behavior. For systems that learn and adapt, the growth and the degree of adaptation depend upon how well the system is engaged with its environment and other contexts influencing its organization. Some systems support other systems, maintaining the other system to prevent failure. The goals of systems theory are to model a system's dynamics, Theory of constraints, constraints, conditions, and relations; and to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quasi-periodic Oscillations
In X-ray astronomy, quasi-periodic oscillation (QPO) is the manner in which the X-ray light from an astronomical object flickers about certain frequencies. In these situations, the X-rays are emitted near the inner edge of an accretion disk in which gas swirls onto a compact object such as a white dwarf, neutron star, or black hole. The QPO phenomenon promises to help astronomers understand the innermost regions of accretion disks and the masses, radii, and spin periods of white dwarfs, neutron stars, and black holes. QPOs could help test Albert Einstein's theory of general relativity which makes predictions that differ most from those of Newtonian gravity when the gravitational force is strongest or when rotation is fastest (when a phenomenon called the Lense–Thirring effect comes into play). However, the various explanations of QPOs remain controversial and the conclusions reached from their study remain provisional. A QPO is identified by performing a power spectrum of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nonlinear Resonance
In physics, nonlinear resonance is the occurrence of resonance in a nonlinear system. In nonlinear resonance the system behaviour – resonance frequency, resonance frequencies and normal mode, modes – depends on the amplitude of the oscillations, while for linear systems this is independent of amplitude. The mixing of modes in non-linear systems is termed resonant interaction. Description Generically two types of resonances have to be distinguished – linear and nonlinear. From the physical point of view, they are defined by whether or not external force coincides with the natural frequency, eigen-frequency of the system (linear and nonlinear resonance correspondingly). Vibrational modes can interact in a resonant interaction when both the energy and momentum of the interacting modes is conserved. The conservation of energy implies that the sum of the frequencies of the modes must sum to zero: : \omega_n=\omega_+ \omega_+ \cdots + \omega_, with possibly different \omega_i=\o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |