|
Quantum Oscillations
In condensed matter physics, quantum oscillations describes a series of related experimental techniques used to map the Fermi surface of a metal in the presence of a strong magnetic field. These techniques are based on the principle of Landau quantization of Fermions moving in a magnetic field. For a gas of free fermions in a strong magnetic field, the energy levels are quantized into bands, called the ''Landau levels'', whose separation is proportional to the strength of the magnetic field. In a quantum oscillation experiment, the external magnetic field is varied, which causes the Landau levels to pass over the Fermi surface, which in turn results in oscillations of the electronic density of states at the Fermi level; this produces oscillations in the many material properties which depend on this, including resistance (the Shubnikov–de Haas effect), Hall resistance, and magnetic susceptibility (the de Haas–van Alphen effect). Observation of quantum oscillations in a material ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Condensed Matter Physics
Condensed matter physics is the field of physics that deals with the macroscopic and microscopic physical properties of matter, especially the solid and liquid State of matter, phases, that arise from electromagnetic forces between atoms and electrons. More generally, the subject deals with condensed phases of matter: systems of many constituents with strong interactions among them. More exotic condensed phases include the superconductivity, superconducting phase exhibited by certain materials at extremely low cryogenic temperatures, the ferromagnetic and antiferromagnetic phases of Spin (physics), spins on crystal lattices of atoms, the Bose–Einstein condensates found in ultracold atomic systems, and liquid crystals. Condensed matter physicists seek to understand the behavior of these phases by experiments to measure various material properties, and by applying the physical laws of quantum mechanics, electromagnetism, statistical mechanics, and other theoretical physics, physic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Condensed Matter Physics
Condensed matter physics is the field of physics that deals with the macroscopic and microscopic physical properties of matter, especially the solid and liquid State of matter, phases, that arise from electromagnetic forces between atoms and electrons. More generally, the subject deals with condensed phases of matter: systems of many constituents with strong interactions among them. More exotic condensed phases include the superconductivity, superconducting phase exhibited by certain materials at extremely low cryogenic temperatures, the ferromagnetic and antiferromagnetic phases of Spin (physics), spins on crystal lattices of atoms, the Bose–Einstein condensates found in ultracold atomic systems, and liquid crystals. Condensed matter physicists seek to understand the behavior of these phases by experiments to measure various material properties, and by applying the physical laws of quantum mechanics, electromagnetism, statistical mechanics, and other theoretical physics, physic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
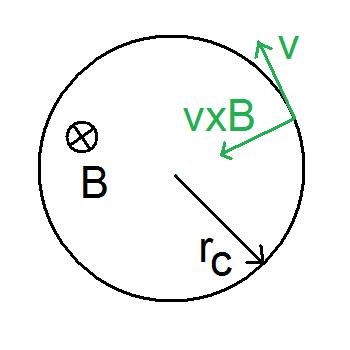
Landau Levels
In quantum mechanics, the energies of cyclotron orbits of charged particles in a uniform magnetic field are quantized to discrete values, thus known as Landau levels. These levels are degenerate, with the number of electrons per level directly proportional to the strength of the applied magnetic field. It is named after the Soviet physicist Lev Landau. Landau quantization contributes towards magnetic susceptibility of metals, known as Landau diamagnetism. Under strong magnetic fields, Landau quantization leads to oscillations in electronic properties of materials as a function of the applied magnetic field known as the De Haas–Van Alphen and Shubnikov–de Haas effects. Landau quantization is a key ingredient in explanation of the integer quantum Hall effect. Derivation Consider a system of non-interacting particles with charge and spin confined to an area in the plane. Apply a uniform magnetic field \mathbf = \begin0\\0\\B\end along the -axis. In SI units, the Hamil ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
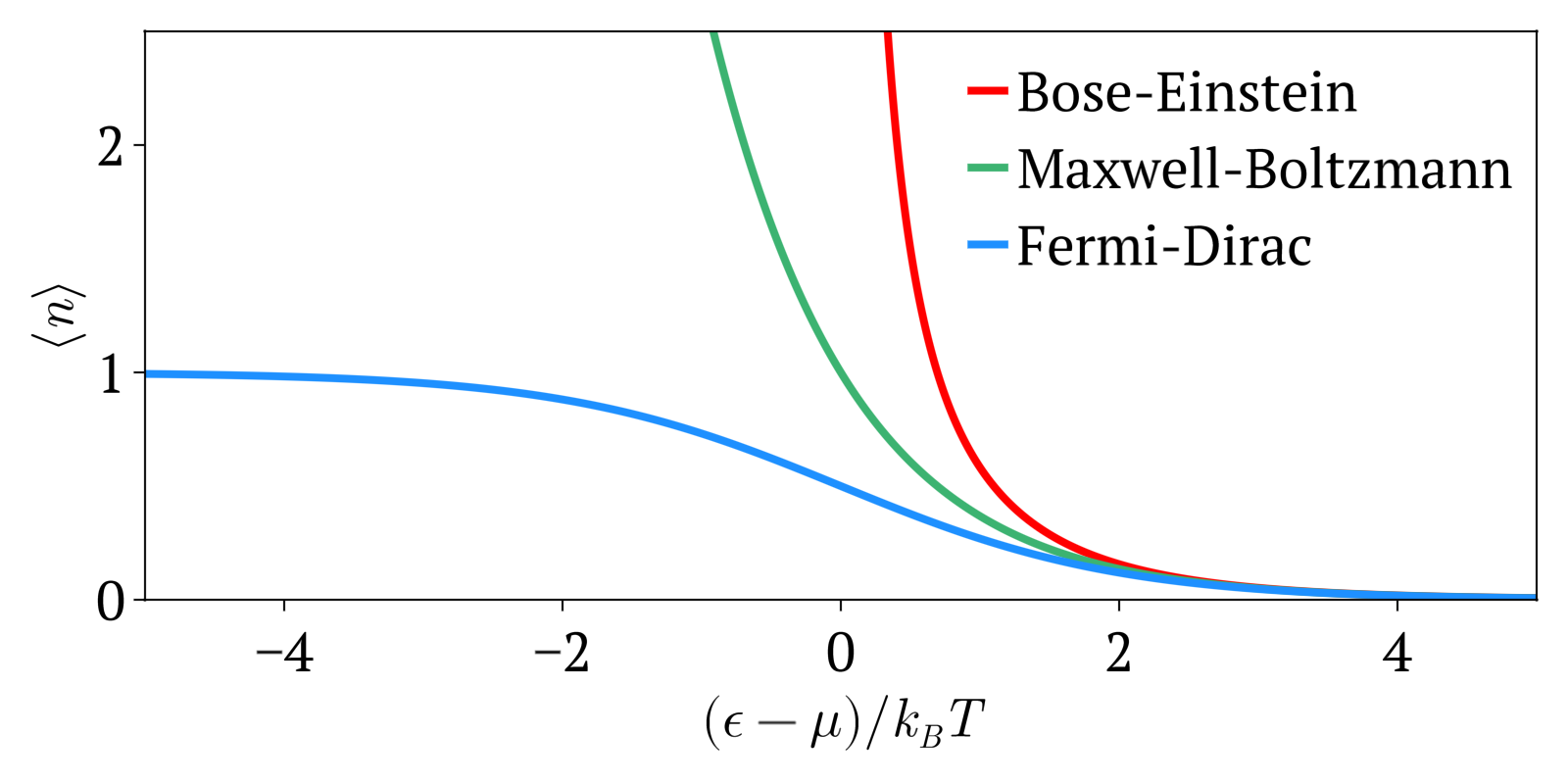
Fermi–Dirac Statistics
Fermi–Dirac statistics is a type of quantum statistics that applies to the physics of a system consisting of many non-interacting, identical particles that obey the Pauli exclusion principle. A result is the Fermi–Dirac distribution of particles over energy states. It is named after Enrico Fermi and Paul Dirac, each of whom derived the distribution independently in 1926. Fermi–Dirac statistics is a part of the field of statistical mechanics and uses the principles of quantum mechanics. Fermi–Dirac statistics applies to identical and indistinguishable particles with half-integer spin (1/2, 3/2, etc.), called fermions, in thermodynamic equilibrium. For the case of negligible interaction between particles, the system can be described in terms of single-particle energy states. A result is the Fermi–Dirac distribution of particles over these states where no two particles can occupy the same state, which has a considerable effect on the properties of the system. Fermi� ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Non-Fermi Liquid
Fermi liquid theory (also known as Landau's Fermi-liquid theory) is a theoretical model of interacting fermions that describes the normal state of the conduction electrons in most metals at sufficiently low temperatures. The theory describes the behavior of many-body systems of particles in which the interactions between particles may be strong. The phenomenological theory of Fermi liquids was introduced by the Soviet physicist Lev Davidovich Landau in 1956, and later developed by Alexei Abrikosov and Isaak Khalatnikov using diagrammatic perturbation theory. The theory explains why some of the properties of an interacting fermion system are very similar to those of the ideal Fermi gas (collection of non-interacting fermions), and why other properties differ. Fermi liquid theory applies most notably to conduction electrons in normal (non-superconducting) metals, and to liquid helium-3. Liquid helium-3 is a Fermi liquid at low temperatures (but not low enough to be in its superflu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
ARPES
Angle-resolved photoemission spectroscopy (ARPES) is an experimental technique used in condensed matter physics to probe the allowed energies and momenta of the electrons in a material, usually a crystalline solid. It is based on the photoelectric effect, in which an incoming photon of sufficient energy ejects an electron from the surface of a material. By directly measuring the kinetic energy and emission angle distributions of the emitted photoelectrons, the technique can map the electronic band structure and Fermi surfaces. ARPES is best suited for the study of one- or two-dimensional materials. It has been used by physicists to investigate high-temperature superconductors, graphene, topological materials, quantum well states, and materials exhibiting charge density waves. ARPES systems consist of a monochromatic light source to deliver a narrow beam of photons, a sample holder connected to a manipulator used to position the sample of a material, and an electron spectro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
YBCO
Yttrium barium copper oxide (YBCO) is a family of crystalline chemical compounds that display high-temperature superconductivity; it includes the first material ever discovered to become superconductivity, superconducting above the boiling point of liquid nitrogen [] at about . Many YBCO compounds have the general formula (also known as Y123), although materials with other Y:Ba:Cu ratios exist, such as (Y124) or (Y247). At present, there is no singularly recognised theory for high-temperature superconductivity. It is part of the more general group of rare-earth barium copper oxides (ReBCO) in which, instead of yttrium, other rare earths are present. History In April 1986, Georg Bednorz and Karl Alexander Müller, Karl Müller, working at IBM Research – Zurich, IBM in Zurich, discovered that certain semiconducting oxides became superconducting at relatively high temperature, in particular, a lanthanum barium copper oxide becomes superconducting at 35 K. This oxide was an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Effective Mass (solid-state Physics)
In solid state physics, a particle's effective mass (often denoted m^*) is the mass that it ''seems'' to have when responding to forces, or the mass that it seems to have when interacting with other identical particles in a thermal distribution. One of the results from the band theory of solids is that the movement of particles in a periodic potential, over long distances larger than the lattice spacing, can be very different from their motion in a vacuum. The effective mass is a quantity that is used to simplify band structures by modeling the behavior of a free particle with that mass. For some purposes and some materials, the effective mass can be considered to be a simple constant of a material. In general, however, the value of effective mass depends on the purpose for which it is used, and can vary depending on a number of factors. For electrons or electron holes in a solid, the effective mass is usually stated as a factor multiplying the rest mass of an electron, ''m'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Oscillations At 100 T
In physics, a quantum (: quanta) is the minimum amount of any physical entity (physical property) involved in an interaction. The fundamental notion that a property can be "quantized" is referred to as "the hypothesis of quantization". This means that the magnitude of the physical property can take on only discrete values consisting of integer multiples of one quantum. For example, a photon is a single quantum of light of a specific frequency (or of any other form of electromagnetic radiation). Similarly, the energy of an electron bound within an atom is quantized and can exist only in certain discrete values. Atoms and matter in general are stable because electrons can exist only at discrete energy levels within an atom. Quantization is one of the foundations of the much broader physics of quantum mechanics. Quantization of energy and its influence on how energy and matter interact (quantum electrodynamics) is part of the fundamental framework for understanding and describing ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fermion
In particle physics, a fermion is a subatomic particle that follows Fermi–Dirac statistics. Fermions have a half-integer spin (spin 1/2, spin , Spin (physics)#Higher spins, spin , etc.) and obey the Pauli exclusion principle. These particles include all quarks and leptons and all composite particles made of an even and odd, odd number of these, such as all baryons and many atoms and atomic nucleus, nuclei. Fermions differ from bosons, which obey Bose–Einstein statistics. Some fermions are elementary particles (such as electrons), and some are composite particles (such as protons). For example, according to the spin-statistics theorem in Theory of relativity, relativistic quantum field theory, particles with integer Spin (physics), spin are bosons. In contrast, particles with half-integer spin are fermions. In addition to the spin characteristic, fermions have another specific property: they possess conserved baryon or lepton quantum numbers. Therefore, what is usually referr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polariton Superfluid
Polariton superfluid is predicted to be a state of the exciton-polaritons system that combines the characteristics of lasers with those of excellent electrical conductors. Researchers look for this state in a solid state optical microcavity coupled with quantum well excitons. The idea is to create an ensemble of particles known as exciton-polaritons and trap them. Wave behavior in this state results in a light beam similar to that from a laser but possibly more energy efficient. Unlike traditional superfluids that need temperatures of approximately ~4 K, the polariton superfluid could in principle be stable at much higher temperatures, and might soon be demonstrable at room temperature. Evidence for polariton superfluidity was reported in by Alberto Amo and coworkers, based on the suppressed scattering of the polaritons during their motion. Although several other researchers are working in the same field, the terminology and conclusions are not completely shared by the differen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |