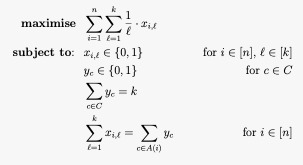|
Proportional Approval Voting
Proportional approval voting (PAV) is a proportional electoral system for multiwinner elections. It is a multiwinner approval method that extends the D'Hondt method of apportionment commonly used to calculate apportionments for party-list proportional representation. However, PAV allows voters to support only the candidates they approve of, rather than being forced to approve or reject all candidates on a given party list. In PAV, voters cast approval ballots marking all candidates they approve of; each voter's ballot is then treated as if all candidates on the ballot were on their own "party list." Seats are then apportioned between candidates in a way that ensures all coalitions are represented proportionally. History PAV is a special case of Thiele's voting rule, proposed by Thorvald N. Thiele. It was used in combination with ranked voting in the Swedish elections from 1909 to 1921 for distributing seats within parties and in local elections. PAV was rediscovered by For ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sequential Proportional Approval Voting
Sequential proportional approval voting (SPAV) or reweighted approval voting (RAV) is an electoral system that extends the concept of approval voting to a multiple winner election. It is a simplified version of proportional approval voting. It is a special case of Thiele's voting rules, proposed by Danish statistician Thorvald N. Thiele in the early 1900s. It was used in Sweden from 1909 to 1921, when it was replaced by a "party-list" style system, and is still used for some local elections. Description Sequential proportional approval voting uses approval voting ballots to elect multiple winners on a round-by-round basis. With approval voting ballots, each voter may support any number of candidates on their ballot as they see fit. For tabulation, each ballot is weighted according to a formula, the candidate with the most support is elected, and the process is repeated until there are no more seats to fill. The aforementioned formula is as follows: W=\frac where E is the n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Example 2
Example may refer to: * ''exempli gratia'' (e.g.), usually read out in English as "for example" * .example, reserved as a domain name that may not be installed as a top-level domain of the Internet ** example.com, example.net, example.org, and example.edu: second-level domain names reserved for use in documentation as examples * HMS ''Example'' (P165), an Archer-class patrol and training vessel of the Royal Navy Arts * ''The Example'', a 1634 play by James Shirley * ''The Example'' (comics), a 2009 graphic novel by Tom Taylor and Colin Wilson * Example (musician), the British dance musician Elliot John Gleave (born 1982) * ''Example'' (album), a 1995 album by American rock band For Squirrels See also * Exemplar (other), a prototype or model which others can use to understand a topic better * Exemplum, medieval collections of short stories to be told in sermons * Eixample The Eixample (, ) is a district of Barcelona between the old city (Ciutat Vella) a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sequential Proportional Approval Voting
Sequential proportional approval voting (SPAV) or reweighted approval voting (RAV) is an electoral system that extends the concept of approval voting to a multiple winner election. It is a simplified version of proportional approval voting. It is a special case of Thiele's voting rules, proposed by Danish statistician Thorvald N. Thiele in the early 1900s. It was used in Sweden from 1909 to 1921, when it was replaced by a "party-list" style system, and is still used for some local elections. Description Sequential proportional approval voting uses approval voting ballots to elect multiple winners on a round-by-round basis. With approval voting ballots, each voter may support any number of candidates on their ballot as they see fit. For tabulation, each ballot is weighted according to a formula, the candidate with the most support is elected, and the process is repeated until there are no more seats to fill. The aforementioned formula is as follows: W=\frac where E is the n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
House Monotonicity
House monotonicity (also called house-size monotonicity) is a property of apportionment methods. These are methods for allocating seats in a parliament among federal states (or among political parties). The property says that, if the number of seats in the "house" (the parliament) increases, and the method is re-activated, then no state (or party) should have fewer seats than it previously had. A method that fails to satisfy house-monotonicity is said to have the Alabama paradox. In the context of committee elections, house monotonicity is often called committee monotonicity. It says that, if the size of the committee increases, then all the candidate that were previously elected, are still elected. House monotonicity is the special case of ''resource monotonicity'' for the setting in which the resource consists of identical discrete items (the seats). Methods violating house-monotonicity An example of a method violating house-monotonicity is the largest remainder method (= H ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Consistency Criterion
A voting system satisfies join-consistency (also called the reinforcement criterion) if combining two sets of votes, both electing ''A'' over ''B'', always results in a combined electorate that ranks ''A'' over ''B''. It is a stronger form of the participation criterion. Systems that fail the consistency criterion (such as instant-runoff voting or Condorcet method, Condorcet methods) are susceptible to the multiple-district paradox, a Pathological (mathematics), pathological behavior where a candidate can win an election without carrying even a single precinct. Conversely, it can be seen as allowing for a particularly egregious kind of gerrymander: it is possible to draw boundaries in such a way that a candidate who wins the overall election fails to carry even a single electoral district. Rules susceptible to the multiple-districts paradox include all Condorcet methods and Instant-runoff voting, instant-runoff (or ranked-choice) voting. Rules that are not susceptible to it includ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polynomial Time
In theoretical computer science, the time complexity is the computational complexity that describes the amount of computer time it takes to run an algorithm. Time complexity is commonly estimated by counting the number of elementary operations performed by the algorithm, supposing that each elementary operation takes a fixed amount of time to perform. Thus, the amount of time taken and the number of elementary operations performed by the algorithm are taken to be related by a constant factor. Since an algorithm's running time may vary among different inputs of the same size, one commonly considers the worst-case time complexity, which is the maximum amount of time required for inputs of a given size. Less common, and usually specified explicitly, is the average-case complexity, which is the average of the time taken on inputs of a given size (this makes sense because there are only a finite number of possible inputs of a given size). In both cases, the time complexity is gener ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Phragmen's Voting Rules
Phragmén's voting rules are rules for multiwinner voting. They allow voters to vote for individual candidates rather than parties, but still guarantee proportional representation. They were published by Lars Edvard Phragmén in French and Swedish between 1893 and 1899, and translated to English by Svante Janson in 2016. Background In multiwinner approval voting, each voter can vote for one or more candidates, and the goal is to select a fixed number ''k'' of winners (where ''k'' may be, for example, the number of parliament members). The question is how to determine the set of winners? * The simplest method is ''multiple non-transferable vote'', in which the ''k'' candidates with the largest number of approvals are elected. But this method tends to select ''k'' candidates of the largest party, leaving the smaller parties with no representation at all. * In the 19th century, there was much discussion regarding election systems that could guarantee proportional representatio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Method Of Equal Shares
The method of equal shares is a proportional method of counting ballots that applies to participatory budgeting, to committee elections, and to simultaneous public decisions. It can be used when the voters vote via approval ballots, ranked ballots or cardinal ballots. It works by dividing the available budget into equal parts that are assigned to each voter. The method is only allowed to use the budget share of a voter to implement projects that the voter voted for. It then repeatedly finds projects that can be afforded using the budget shares of the supporting voters. In contexts other than participatory budgeting, the method works by equally dividing an abstract budget of "voting power". In 2023, the method of equal shares was being used in a participatory budgeting program in the Polish city of Wieliczka. The program, known as Green Million (''Zielony Milion''), was set to distribute 1 million złoty to ecological projects proposed by residents of the city. It was also used ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pigou–Dalton Principle
The Pigou–Dalton principle (PDP) is a principle in welfare economics, particularly in cardinal welfarism. Named after Arthur Cecil Pigou and Hugh Dalton, it is a condition on social welfare functions. It says that, all other things being equal, a social welfare function should prefer allocations that are more equitable. In other words, a transfer of some defined variable (for example utility or income) from the rich to the poor is desirable, as long as it does not bring the rich to a poorer situation than the poor. Formally, let u=(u_1,u_2,\dots,u_n) and u'=(u'_1,u'_2,\dots,u'_n) be two utility profiles. Suppose that at the first profile: :u_1 [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Core (game Theory)
In cooperative game theory, the core is the set of feasible allocations or imputations where no coalition of agents can benefit by breaking away from the grand coalition. An allocation is said to be in the ''core'' of a game if there is no coalition that can improve upon it. The core is then the set of all feasible allocations. Origin The idea of the core already appeared in the writings of , at the time referred to as the ''contract curve''. Even though von Neumann and Morgenstern considered it an interesting concept, they only worked with zero-sum games where the core is always empty. The modern definition of the core is due to Gillies. Definition Consider a transferable utility cooperative game (N,v) where N denotes the set of players and v is the characteristic function. An imputation x\in\mathbb^N is ''dominated'' by another imputation y if there exists a coalition C, such that each player in C weakly-prefers y (x_i\leq y_i for all i\in C) and there exists i\in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Proportional Justified Representation
Justified representation (JR) is a criterion of fairness in multiwinner approval voting. It can be seen as an adaptation of the proportional representation criterion to approval voting. Background Proportional representation (PR) is an important consideration in designing electoral systems. It means that the various groups and sectors in the population should be represented in the parliament in proportion to their size. The most common system for ensuring proportional representation is the party-list system. In this system, the candidates are partitioned into parties, and each citizen votes for a single party. Each party receives a number of seats proportional to the number of citizens who voted for it. For example, for a parliament with 10 seats, if exactly 50% of the citizens vote for party A, exactly 30% vote for party B, and exactly 20% vote for party C, then proportional representation requires that the parliament contains exactly 5 candidates from party A, exactly 3 can ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |