|
Proof That π Is Irrational
In the 1760s, Johann Heinrich Lambert was the first to prove that the number is irrational, meaning it cannot be expressed as a fraction a/b, where a and b are both integers. In the 19th century, Charles Hermite found a proof that requires no prerequisite knowledge beyond basic calculus. Three simplifications of Hermite's proof are due to Mary Cartwright, Ivan Niven, and Nicolas Bourbaki. Another proof, which is a simplification of Lambert's proof, is due to Miklós Laczkovich. Many of these are proofs by contradiction. In 1882, Ferdinand von Lindemann proved that \pi is not just irrational, but transcendental as well. Lambert's proof In 1761, Johann Heinrich Lambert proved that \pi is irrational by first showing that this continued fraction expansion holds: :\tan(x) = \cfrac. Then Lambert proved that if x is non-zero and rational, then this expression must be irrational. Since \tan\tfrac\pi4 =1, it follows that \tfrac\pi4 is irrational, and thus \pi is also irrational. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Johann Heinrich Lambert
Johann Heinrich Lambert (; ; 26 or 28 August 1728 – 25 September 1777) was a polymath from the Republic of Mulhouse, at that time allied to the Switzerland, Swiss Confederacy, who made important contributions to the subjects of mathematics, physics (particularly optics), philosophy, astronomy and map projections. Biography Lambert was born in 1728 into a Huguenot family in the city of Mulhouse, nowadays in Alsace, France, at that time a city-state allied to the Swiss Confederacy. Some sources give 26 August as his birth date and others 28 August. Leaving school at 12, he continued to study in his free time while undertaking a series of jobs. These included assistant to his father (a tailor), a clerk at a nearby iron works, a private tutor, secretary to the editor of ''Basler Zeitung'' and, at the age of 20, private tutor to the sons of Count Salis in Chur. Travelling Europe with his charges (1756–1758) allowed him to meet established mathematicians in the German states, Th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
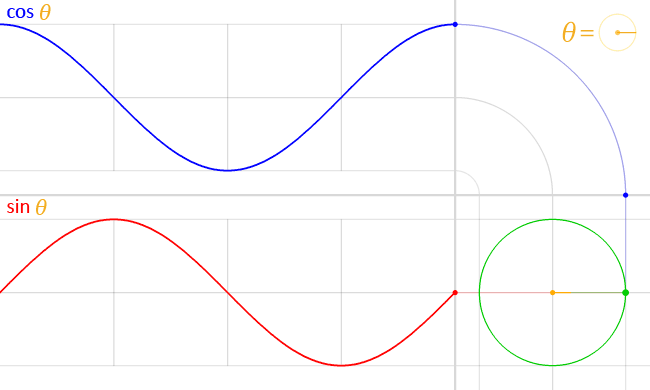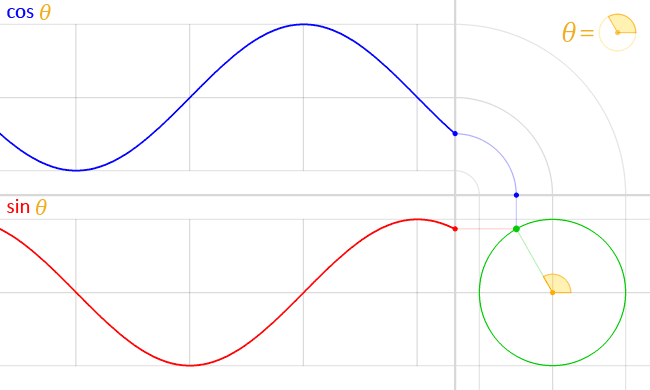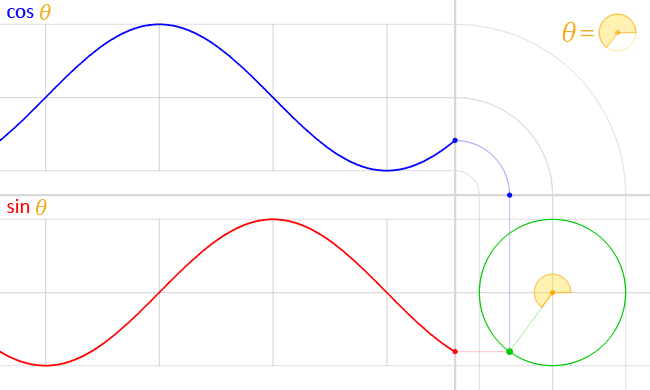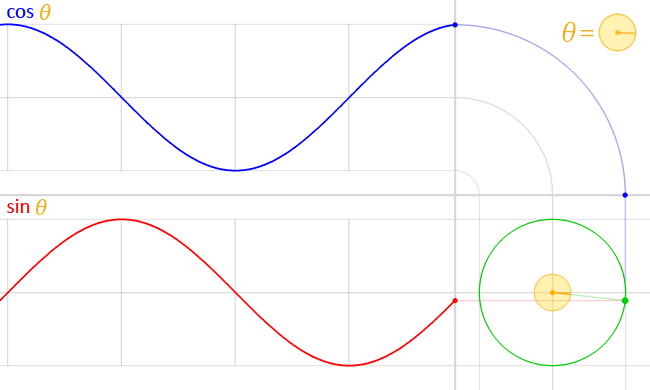
Cosine
In mathematics, sine and cosine are trigonometric functions of an angle. The sine and cosine of an acute angle are defined in the context of a right triangle: for the specified angle, its sine is the ratio of the length of the side opposite that angle to the length of the longest side of the triangle (the hypotenuse), and the cosine is the ratio of the length of the adjacent leg to that of the hypotenuse. For an angle \theta, the sine and cosine functions are denoted as \sin(\theta) and \cos(\theta). The definitions of sine and cosine have been extended to any real number, real value in terms of the lengths of certain line segments in a unit circle. More modern definitions express the sine and cosine as Series (mathematics), infinite series, or as the solutions of certain differential equations, allowing their extension to arbitrary positive and negative values and even to complex numbers. The sine and cosine functions are commonly used to model periodic function, periodic pheno ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sine
In mathematics, sine and cosine are trigonometric functions of an angle. The sine and cosine of an acute angle are defined in the context of a right triangle: for the specified angle, its sine is the ratio of the length of the side opposite that angle to the length of the longest side of the triangle (the hypotenuse), and the cosine is the ratio of the length of the adjacent leg to that of the hypotenuse. For an angle \theta, the sine and cosine functions are denoted as \sin(\theta) and \cos(\theta). The definitions of sine and cosine have been extended to any real value in terms of the lengths of certain line segments in a unit circle. More modern definitions express the sine and cosine as infinite series, or as the solutions of certain differential equations, allowing their extension to arbitrary positive and negative values and even to complex numbers. The sine and cosine functions are commonly used to model periodic phenomena such as sound and light waves, the posit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polynomial
In mathematics, a polynomial is a Expression (mathematics), mathematical expression consisting of indeterminate (variable), indeterminates (also called variable (mathematics), variables) and coefficients, that involves only the operations of addition, subtraction, multiplication and exponentiation to nonnegative integer powers, and has a finite number of terms. An example of a polynomial of a single indeterminate is . An example with three indeterminates is . Polynomials appear in many areas of mathematics and science. For example, they are used to form polynomial equations, which encode a wide range of problems, from elementary word problem (mathematics education), word problems to complicated scientific problems; they are used to define polynomial functions, which appear in settings ranging from basic chemistry and physics to economics and social science; and they are used in calculus and numerical analysis to approximate other functions. In advanced mathematics, polynomials are ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Recurrence Relation
In mathematics, a recurrence relation is an equation according to which the nth term of a sequence of numbers is equal to some combination of the previous terms. Often, only k previous terms of the sequence appear in the equation, for a parameter k that is independent of n; this number k is called the ''order'' of the relation. If the values of the first k numbers in the sequence have been given, the rest of the sequence can be calculated by repeatedly applying the equation. In ''linear recurrences'', the th term is equated to a linear function of the k previous terms. A famous example is the recurrence for the Fibonacci numbers, F_n=F_+F_ where the order k is two and the linear function merely adds the two previous terms. This example is a linear recurrence with constant coefficients, because the coefficients of the linear function (1 and 1) are constants that do not depend on n. For these recurrences, one can express the general term of the sequence as a closed-form expression o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cambridge University
The University of Cambridge is a Public university, public collegiate university, collegiate research university in Cambridge, England. Founded in 1209, the University of Cambridge is the List of oldest universities in continuous operation, world's third-oldest university in continuous operation. The university's founding followed the arrival of scholars who left the University of Oxford for Cambridge after a dispute with local townspeople. The two ancient university, ancient English universities, although sometimes described as rivals, share many common features and are often jointly referred to as Oxbridge. In 1231, 22 years after its founding, the university was recognised with a royal charter, granted by Henry III of England, King Henry III. The University of Cambridge includes colleges of the University of Cambridge, 31 semi-autonomous constituent colleges and List of institutions of the University of Cambridge#Schools, Faculties, and Departments, over 150 academic departm ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Harold Jeffreys
Sir Harold Jeffreys, FRS (22 April 1891 – 18 March 1989) was a British geophysicist who made significant contributions to mathematics and statistics. His book, ''Theory of Probability'', which was first published in 1939, played an important role in the revival of the objective Bayesian view of probability. Education Jeffreys was born in Fatfield, County Durham, England, the son of Robert Hal Jeffreys, headmaster of Fatfield Church School, and his wife, Elizabeth Mary Sharpe, a school teacher. He was educated at his father's school and at Rutherford Technical College, then studied at Armstrong College in Newcastle upon Tyne (at that time part of the University of Durham) and with the University of London External Programme.Cook, Alan ev.br>"Jeffreys, Sir Harold (1891–1989)" ''Oxford Dictionary of National Biography'', Oxford University Press, 2004; online edition, September 2004. Retrieved 1 January 2023. Jeffreys subsequently won a scholarship to study the Mathem ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Transcendental Number
In mathematics, a transcendental number is a real or complex number that is not algebraic: that is, not the root of a non-zero polynomial with integer (or, equivalently, rational) coefficients. The best-known transcendental numbers are and . The quality of a number being transcendental is called transcendence. Though only a few classes of transcendental numbers are known, partly because it can be extremely difficult to show that a given number is transcendental. Transcendental numbers are not rare: indeed, almost all real and complex numbers are transcendental, since the algebraic numbers form a countable set, while the set of real numbers and the set of complex numbers are both uncountable sets, and therefore larger than any countable set. All transcendental real numbers (also known as real transcendental numbers or transcendental irrational numbers) are irrational numbers, since all rational numbers are algebraic. The converse is not true: Not all irrational numbers are ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Leibniz Integral Rule
In calculus, the Leibniz integral rule for differentiation under the integral sign, named after Gottfried Wilhelm Leibniz, states that for an integral of the form \int_^ f(x,t)\,dt, where -\infty < a(x), b(x) < \infty and the integrands are functions dependent on the derivative of this integral is expressible as where the partial derivative indicates that inside the integral, only the variation of with is considered in taking the derivative. In the special case where the functions and |
Integration By Parts
In calculus, and more generally in mathematical analysis, integration by parts or partial integration is a process that finds the integral of a product of functions in terms of the integral of the product of their derivative and antiderivative. It is frequently used to transform the antiderivative of a product of functions into an antiderivative for which a solution can be more easily found. The rule can be thought of as an integral version of the product rule of differentiation; it is indeed derived using the product rule. The integration by parts formula states: \begin \int_a^b u(x) v'(x) \, dx & = \Big (x) v(x)\Biga^b - \int_a^b u'(x) v(x) \, dx\\ & = u(b) v(b) - u(a) v(a) - \int_a^b u'(x) v(x) \, dx. \end Or, letting u = u(x) and du = u'(x) \,dx while v = v(x) and dv = v'(x) \, dx, the formula can be written more compactly: \int u \, dv \ =\ uv - \int v \, du. The former expression is written as a definite integral and the latter is written as an indefinite ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Natural Number
In mathematics, the natural numbers are the numbers 0, 1, 2, 3, and so on, possibly excluding 0. Some start counting with 0, defining the natural numbers as the non-negative integers , while others start with 1, defining them as the positive integers Some authors acknowledge both definitions whenever convenient. Sometimes, the whole numbers are the natural numbers as well as zero. In other cases, the ''whole numbers'' refer to all of the integers, including negative integers. The counting numbers are another term for the natural numbers, particularly in primary education, and are ambiguous as well although typically start at 1. The natural numbers are used for counting things, like "there are ''six'' coins on the table", in which case they are called ''cardinal numbers''. They are also used to put things in order, like "this is the ''third'' largest city in the country", which are called ''ordinal numbers''. Natural numbers are also used as labels, like Number (sports), jersey ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Induction
Mathematical induction is a method for mathematical proof, proving that a statement P(n) is true for every natural number n, that is, that the infinitely many cases P(0), P(1), P(2), P(3), \dots all hold. This is done by first proving a simple case, then also showing that if we assume the claim is true for a given case, then the next case is also true. Informal metaphors help to explain this technique, such as falling dominoes or climbing a ladder: A proof by induction consists of two cases. The first, the base case, proves the statement for n = 0 without assuming any knowledge of other cases. The second case, the induction step, proves that ''if'' the statement holds for any given case n = k, ''then'' it must also hold for the next case n = k + 1. These two steps establish that the statement holds for every natural number n. The base case does not necessarily begin with n = 0, but often with n = 1, and possibly with any fixed natural number n = N, establishing the trut ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |