|
Process Calculi
In computer science, the process calculi (or process algebras) are a diverse family of related approaches for formally modelling concurrent systems. Process calculi provide a tool for the high-level description of interactions, communications, and synchronizations between a collection of independent agents or processes. They also provide algebraic laws that allow process descriptions to be manipulated and analyzed, and permit formal reasoning about equivalences between processes (e.g., using bisimulation). Leading examples of process calculi include Communicating Sequential Processes, CSP, Calculus of Communicating Systems, CCS, Algebra of Communicating Processes, ACP, and Language Of Temporal Ordering Specification, LOTOS. More recent additions to the family include the Pi-calculus, π-calculus, the ambient calculus, PEPA, the fusion calculus and the join-calculus. Essential features While the variety of existing process calculi is very large (including variants that incorporat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Computer Science
Computer science is the study of computation, information, and automation. Computer science spans Theoretical computer science, theoretical disciplines (such as algorithms, theory of computation, and information theory) to Applied science, applied disciplines (including the design and implementation of Computer architecture, hardware and Software engineering, software). Algorithms and data structures are central to computer science. The theory of computation concerns abstract models of computation and general classes of computational problem, problems that can be solved using them. The fields of cryptography and computer security involve studying the means for secure communication and preventing security vulnerabilities. Computer graphics (computer science), Computer graphics and computational geometry address the generation of images. Programming language theory considers different ways to describe computational processes, and database theory concerns the management of re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
π-calculus
In theoretical computer science, the -calculus (or pi-calculus) is a process calculus. The -calculus allows channel names to be communicated along the channels themselves, and in this matter, it is able to describe concurrent computations whose network configuration may change during the computation. The -calculus has few terms and is a small, yet expressive language (see ). Functional programs can be encoded into the -calculus, and the encoding emphasises the dialogue nature of computation, drawing connections with game semantics. Extensions of the -calculus, such as the spi calculus and applied , have been successful in reasoning about cryptographic protocols. Beside the original use in describing concurrent systems, the -calculus has also been used to reason through business processes,OMG Specification (2011)"Business Process Model and Notation (BPMN) Version 2.0" ''Object Management Group''. p.21 molecular biology. and autonomous agents in artificial intelligence. Inform ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jan Bergstra
Johannes Aldert "Jan" Bergstra (born 1951) is a Dutch computer scientist. His work has focused on logic and the theoretical foundations of software engineering, especially on formal methods for system design. He is best known as an expert on algebraic methods for the specification of data and computational processes in general. Biography Jan Bergstra was born in 1951 in Rotterdam, the son of Tjeerd Bergstra and Johanna Bisschop.Jan A. Bergstra (2009)Curriculum Vitae Jan Aldert Bergstra at ''uva.nl''. October 20, 2009. Accessed August 30, 2013 He was educated at the Montessori Lyceum Rotterdam (gymnasium beta) and then studied mathematics at Utrecht University, starting in 1969. After an MSc he wrote a PhD thesis, defended in 1976, on recursion theory in higher types, under the supervision of Dirk van Dalen. Bergstra held posts at the Institute of Applied Mathematics and Computer Science of the University of Leiden (1976–82), and the Centrum Wiskunde & Informatica (CWI) in Am ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Robin Milner
Arthur John Robin Gorell Milner (13 January 1934 – 20 March 2010) was a British computer scientist, and a Turing Award winner.Obituary – Professor Robin Milner: computer scientist '''', 31 March 2010. Life, education and career Milner was born in , near , |
Actor Model
The actor model in computer science is a mathematical model of concurrent computation that treats an ''actor'' as the basic building block of concurrent computation. In response to a message it receives, an actor can: make local decisions, create more actors, send more messages, and determine how to respond to the next message received. Actors may modify their own private state, but can only affect each other indirectly through messaging (removing the need for lock-based synchronization). The actor model originated in 1973. It has been used both as a framework for a theoretical understanding of computation and as the theoretical basis for several practical implementations of concurrent systems. The relationship of the model to other work is discussed in actor model and process calculi. History According to Carl Hewitt, unlike previous models of computation, the actor model was inspired by physics, including general relativity and quantum mechanics. It was also influenced ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
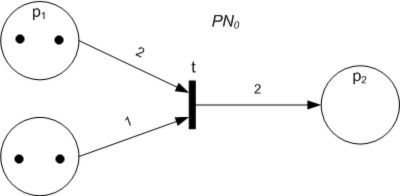
Petri Net
A Petri net, also known as a place/transition net (PT net), is one of several mathematical modeling languages for the description of distributed systems. It is a class of discrete event dynamic system. A Petri net is a directed bipartite graph that has two types of elements: places and transitions. Place elements are depicted as white circles and transition elements are depicted as rectangles. A place can contain any number of tokens, depicted as black circles. A transition is enabled if all places connected to it as inputs contain at least one token. Some sources state that Petri nets were invented in August 1939 by Carl Adam Petri — at the age of 13 — for the purpose of describing chemical processes. Like industry standards such as UML activity diagrams, Business Process Model and Notation, and event-driven process chains, Petri nets offer a graphical notation for stepwise processes that include choice, iteration, and concurrent execution. Unlike these standards, Pet ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lambda Calculus
In mathematical logic, the lambda calculus (also written as ''λ''-calculus) is a formal system for expressing computability, computation based on function Abstraction (computer science), abstraction and function application, application using variable Name binding, binding and Substitution (algebra), substitution. Untyped lambda calculus, the topic of this article, is a universal machine, a model of computation that can be used to simulate any Turing machine (and vice versa). It was introduced by the mathematician Alonzo Church in the 1930s as part of his research into the foundations of mathematics. In 1936, Church found a formulation which was #History, logically consistent, and documented it in 1940. Lambda calculus consists of constructing #Lambda terms, lambda terms and performing #Reduction, reduction operations on them. A term is defined as any valid lambda calculus expression. In the simplest form of lambda calculus, terms are built using only the following rules: # x: A ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Turing Machine
A Turing machine is a mathematical model of computation describing an abstract machine that manipulates symbols on a strip of tape according to a table of rules. Despite the model's simplicity, it is capable of implementing any computer algorithm. The machine operates on an infinite memory tape divided into discrete mathematics, discrete cells, each of which can hold a single symbol drawn from a finite set of symbols called the Alphabet (formal languages), alphabet of the machine. It has a "head" that, at any point in the machine's operation, is positioned over one of these cells, and a "state" selected from a finite set of states. At each step of its operation, the head reads the symbol in its cell. Then, based on the symbol and the machine's own present state, the machine writes a symbol into the same cell, and moves the head one step to the left or the right, or halts the computation. The choice of which replacement symbol to write, which direction to move the head, and whet ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Μ-recursive Function
In mathematical logic and computer science, a general recursive function, partial recursive function, or μ-recursive function is a partial function from natural numbers to natural numbers that is "computable" in an intuitive sense – as well as in a formal one. If the function is total, it is also called a total recursive function (sometimes shortened to recursive function). In computability theory, it is shown that the μ-recursive functions are precisely the functions that can be computed by Turing machines (this is one of the theorems that supports the Church–Turing thesis). The μ-recursive functions are closely related to primitive recursive functions, and their inductive definition (below) builds upon that of the primitive recursive functions. However, not every total recursive function is a primitive recursive function—the most famous example is the Ackermann function. Other equivalent classes of functions are the functions of lambda calculus and the functions tha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Discrete Time And Continuous Time
In mathematical dynamics, discrete time and continuous time are two alternative frameworks within which variables that evolve over time are modeled. Discrete time Discrete time views values of variables as occurring at distinct, separate "points in time", or equivalently as being unchanged throughout each non-zero region of time ("time period")—that is, time is viewed as a discrete variable. Thus a non-time variable jumps from one value to another as time moves from one time period to the next. This view of time corresponds to a digital clock that gives a fixed reading of 10:37 for a while, and then jumps to a new fixed reading of 10:38, etc. In this framework, each variable of interest is measured once at each time period. The number of measurements between any two time periods is finite. Measurements are typically made at sequential integer values of the variable "time". A discrete signal or discrete-time signal is a time series consisting of a sequence of quantities. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Replication (computing)
Replication in computing refers to maintaining multiple copies of data, processes, or resources to ensure consistency across redundant components. This fundamental technique spans databases, file systems, and distributed systems, serving to improve availability, fault-tolerance, accessibility, and performance. Through replication, systems can continue operating when components fail ( failover), serve requests from geographically distributed locations, and balance load across multiple machines. The challenge lies in maintaining consistency between replicas while managing the fundamental tradeoffs between data consistency, system availability, and network partition tolerance – constraints known as the CAP theorem. Terminology Replication in computing can refer to: * ''Data replication'', where the same data is stored on multiple storage devices * ''Computation replication'', where the same computing task is executed many times. Computational tasks may be: ** ''Replicated in s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |