|
Prismanes
The prismanes are a class of hydrocarbon compounds consisting of prism-like polyhedra of various numbers of sides on the polygonal base. Chemically, it is a series of fused cyclobutane rings (a ladderane, with all- cis/all- syn geometry) that wraps around to join its ends and form a band, with cycloalkane edges. Their chemical formula is (C2H2)n, where ''n'' is the number of cyclobutane sides (the size of the cycloalkane base), and that number also forms the basis for a system of nomenclature within this class. The first few chemicals in this class are: Triprismane, tetraprismane, and pentaprismane have been synthesized and studied experimentally, and many higher members of the series have been studied using computer models. The first several members do indeed have the geometry of a regular prism, with flat ''n''-gon bases. As ''n'' becomes increasingly large, however, modeling experiments find that highly symmetric geometry is no longer stable, and the molecule distorts into l ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Asterane
Asteranes are members of a series of cage hydrocarbons consisting of two cycloalkane rings linked to each other by methylene groups. Each linking face is thus a cyclohexane, which has a boat conformation. They can be considered as homologues of the prismanes, but with a carbon linker between the faces rather than direct bonding. The molecules having triangular and square bases, sterane and sterane, have been synthesized and studied experimentally, and many higher members of the series have been studied using computer models Computer simulation is the process of mathematical modelling, performed on a computer, which is designed to predict the behaviour of, or the outcome of, a real-world or physical system. The reliability of some mathematical models can be det .... Modeling experiments predict that the highly symmetric geometry is no longer stable starting with sterane. References {{reflist Hydrocarbons ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
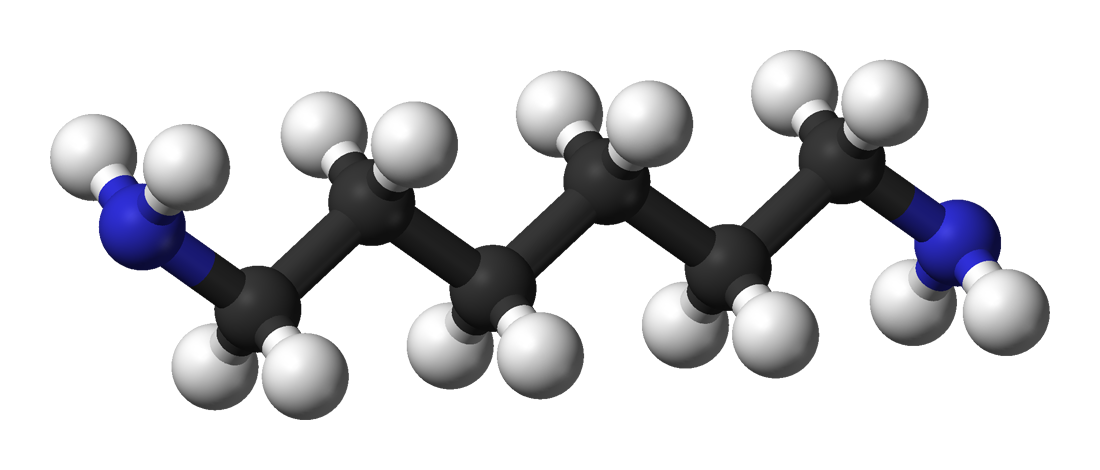
Ladderane
In chemistry, a ladderane is an organic molecule containing two or more fused cyclobutane rings. The name arises from the resemblance of a series of fused cyclobutane rings to a ladder. Numerous synthetic approaches have been developed for the synthesis of ladderane compounds of various lengths. The mechanisms often involve + 2photocycloadditions, a useful reaction for creating strained 4-membered rings. Naturally occurring ladderanes have been identified as major components of the anammoxosome membrane of the anammox bacteria, phylum ''Planctomycetota''. Nomenclature Chain length Synthetic approaches have yielded ladderanes of varying lengths. A classification system has been developed to describe ladderanes based on the number of consecutive rings. The length of the ladderane is described by the number in brackets that precedes the word "ladderane". This is equal to the number of bonds shared by two cyclobutanes (''n'') plus 1. A ladderane of 3 or more units can connect in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prismane
Prismane or 'Ladenburg benzene' is a polycyclic hydrocarbon with the formula C6H6. It is an isomer of benzene, specifically a valence isomer. Prismane is far less stable than benzene. The carbon (and hydrogen) atoms of the prismane molecule are arranged in the shape of a six-atom triangular prism—this compound is the parent and simplest member of the prismanes class of molecules. Albert Ladenburg proposed this structure for the compound now known as benzene. The compound was not synthesized until 1973. History In the mid 19th century, investigators proposed several possible structures for benzene which were consistent with its empirical formula, C6H6, which had been determined by combustion analysis. The first, which was proposed by Kekulé in 1865, later proved to be closest to the true structure of benzene. This structure inspired several others to draw structures that were consistent with benzene's empirical formula; for example, Ladenburg proposed prismane, Dewar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cubane
Cubane () is a synthetic hydrocarbon compound that consists of eight carbon atoms arranged at the corners of a Cube (geometry), cube, with one hydrogen atom attached to each carbon atom. A solid crystalline substance, cubane is one of the Platonic hydrocarbons and a member of the prismanes. It was first synthesized in 1964 by Philip Eaton and Thomas Cole. Before this work, Eaton believed that cubane would be impossible to synthesize due to the "required 90 degree molecular geometry, bond angles". The cubic shape requires the carbon atoms to adopt an unusually sharp 90° bonding angle, which would be highly strain (chemistry), strained as compared to the 109.45° angle of a tetrahedral geometry, tetrahedral carbon. Once formed, cubane is quite kinetic stability, kinetically stable, due to a lack of readily available decomposition paths. It is the simplest hydrocarbon with octahedral symmetry. Having high potential energy but kinetic stability makes cubane and its derivative compoun ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Allotropes Of Carbon
Carbon is capable of forming many allotropes (structurally different forms of the same element) due to its valency. Well-known forms of carbon include diamond and graphite. In recent decades, many more allotropes have been discovered and researched, including ball shapes such as buckminsterfullerene and sheets such as graphene. Larger-scale structures of carbon include carbon nano tube, nanotubes, nanobuds and nanoribbons. Other unusual forms of carbon exist at very high temperatures or extreme pressures. Around 500 hypothetical 3‑periodic allotropes of carbon are known at the present time, according to the Samara Carbon Allotrope Database (SACADA). Diamond Diamond is a well-known allotrope of carbon. The hardness, extremely high refractive index, and high dispersion of light make diamond useful for industrial applications and for jewelry. Diamond is the hardest known natural mineral. This makes it an excellent abrasive and makes it hold polish and luster extre ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cyclohexane
Cyclohexane is a cycloalkane with the molecular formula . Cyclohexane is non-polar. Cyclohexane is a colorless, flammable liquid with a distinctive detergent-like odor, reminiscent of cleaning products (in which it is sometimes used). Cyclohexane is mainly used for the industrial production of adipic acid and caprolactam, which are precursors to nylon. Cyclohexyl () is the alkyl substituent of cyclohexane and is abbreviated Cy. Production Modern On an industrial scale, cyclohexane is produced by hydrogenation of benzene in the presence of a Raney nickel catalyst. Producers of cyclohexane account for approximately 11.4% of global demand for benzene. The reaction is highly exothermic, with ΔH(500 K) = -216.37 kJ/mol. Dehydrogenation commenced noticeably above 300 °C, reflecting the favorable entropy for dehydrogenation. : Early Unlike benzene, cyclohexane is not found in natural resources such as coal. For this reason, early investigators synthesized their cyclohex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Methylene Group
In organic chemistry, a methylene group is any part of a molecule that consists of two hydrogen atoms bound to a carbon Carbon () is a chemical element with the symbol C and atomic number 6. It is nonmetallic and tetravalent—its atom making four electrons available to form covalent chemical bonds. It belongs to group 14 of the periodic table. Carbon makes ... atom, which is connected to the remainder of the molecule by two single bonds. The group may be represented as , where the '<' denotes the two bonds. This can equally well be represented as . This stands in contrast to a situation where the carbon atom is bound to the rest of the molecule by a double bond, which is preferably called a methylidene group, represented . Formerly the methylene name was used for both isomers. The name “ [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Flag Of Israel
The flag of Israel ( he, דגל ישראל '; ar, علم إسرائيل ') was adopted on 28 October 1948, five months after the establishment of the State of Israel. It depicts a blue hexagram on a white background, between two horizontal blue stripes. The Israeli flag legislation states that the official measurements are 160 × 220 cm. Therefore, the official proportions are 8:11. Variants can be found at a wide range of proportions, with 2:3 being common. The blue colour is described as "dark sky-blue",Israel Ministry of Foreign Affairs publicatioThe Flag and the Emblem by art historian Alec Mishory, wherein he quotes "The Provisional Council of State Proclamation of the Flag of the State of Israel" made on October 28, 1948 by Joseph Sprinzak, Speaker. and varies from flag to flag, ranging from a hue of pure blue, sometimes shaded almost as dark as navy blue, to hues about 75% toward pure cyan and shades as light as very light blue. An early version of the flag was dis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Flag Of Switzerland
The national flag of Switzerland (german: Schweizerfahne; french: drapeau de la Suisse; it, bandiera svizzera; rm, bandiera da la Svizra) displays a white cross in the centre of a square red field. The white cross is known as the Swiss cross or the federal cross. Its arms are equilateral, and their ratio of length to width is 7:6. The size of the cross in relation to the field was set in 2017 as 5:8.Appendix 2 ''Wappenschutzgesetz'' (SR 232.21), 21 June 2013 (effective 1 January 2017) ength of an arm: 7 units, width o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometric Isomer
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is called a ''geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point, line, plane, distance, angle, surface, and curve, as fundamental concepts. During the 19th century several discoveries enlarged dramatically the scope of geometry. One of the oldest such discoveries is Carl Friedrich Gauss' ("remarkable theorem") that asserts roughly that the Gaussian curvature of a surface is independent from any specific embedding in a Euclidean space. This implies that surfaces can be studied ''intrinsically'', that is, as stand-alone spaces, and has been expanded into the theory of manifolds and Riemannian geometry. Later in the 19th century, it appeared that geometries ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dodecagon
In geometry, a dodecagon or 12-gon is any twelve-sided polygon. Regular dodecagon A regular dodecagon is a figure with sides of the same length and internal angles of the same size. It has twelve lines of reflective symmetry and rotational symmetry of order 12. A regular dodecagon is represented by the Schläfli symbol and can be constructed as a truncated hexagon, t, or a twice-truncated triangle, tt. The internal angle at each vertex of a regular dodecagon is 150°. Area The area of a regular dodecagon of side length ''a'' is given by: :\begin A & = 3 \cot\left(\frac \right) a^2 = 3 \left(2+\sqrt \right) a^2 \\ & \simeq 11.19615242\,a^2 \end And in terms of the apothem ''r'' (see also inscribed figure), the area is: :\begin A & = 12 \tan\left(\frac\right) r^2 = 12 \left(2-\sqrt \right) r^2 \\ & \simeq 3.2153903\,r^2 \end In terms of the circumradius ''R'', the area is: :A = 6 \sin\left(\fr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
_Ladderane.png)