|
Polytropic Process
A polytropic process is a thermodynamic process that obeys the relation: p V^ = C where ''p'' is the pressure, ''V'' is volume, ''n'' is the polytropic index, and ''C'' is a constant. The polytropic process equation describes expansion and compression processes which include heat transfer. Particular cases Some specific values of ''n'' correspond to particular cases: * n=0 for an isobaric process, * n=+\infty for an isochoric process. In addition, when the ideal gas law applies: * n=1 for an isothermal process, * n=\gamma for an isentropic process. Where \gamma is the ratio of the heat capacity at constant pressure (C_P) to heat capacity at constant volume (C_V). Equivalence between the polytropic coefficient and the ratio of energy transfers For an ideal gas in a closed system undergoing a slow process with negligible changes in kinetic and potential energy the process is polytropic, such that p v^ = C where ''C'' is a constant, K = \frac, \gamma = \frac, and with the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Biogeography
Biogeography is the study of the species distribution, distribution of species and ecosystems in geography, geographic space and through evolutionary history of life, geological time. Organisms and biological community (ecology), communities often vary in a regular fashion along geographic gradients of latitude, elevation, allopatric speciation, isolation and habitat species-area curve, area. Phytogeography is the branch of biogeography that studies the distribution of plants. Zoogeography is the branch that studies distribution of animals. Mycogeography is the branch that studies distribution of fungi, such as mushrooms. Knowledge of spatial variation in the numbers and types of organisms is as vital to us today as it was to our early human ancestors, as we adapt to heterogeneous but geographically predictable Natural environment, environments. Biogeography is an integrative field of inquiry that unites concepts and information from ecology, evolutionary biology, taxonomy (bio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Explosion
An explosion is a rapid expansion in volume of a given amount of matter associated with an extreme outward release of energy, usually with the generation of high temperatures and release of high-pressure gases. Explosions may also be generated by a slower expansion that would normally not be forceful, but is not allowed to expand, so that when whatever is containing the expansion is broken by the pressure that builds as the matter inside tries to expand, the matter expands forcefully. An example of this is a Volcano, volcanic eruption created by the expansion of magma in a magma chamber as it rises to the surface. Supersonic explosions created by high explosives are known as detonations and travel through shock waves. wikt:subsonic, Subsonic explosions are created by low explosives through a slower combustion process known as deflagration. Causes For an explosion to occur, there must be a rapid, forceful expansion of matter. There are numerous ways this can happen, both natura ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compressor
A compressor is a mechanical device that increases the pressure of a gas by reducing its volume. An air compressor is a specific type of gas compressor. Many compressors can be staged, that is, the gas is compressed several times in steps or stages, to increase discharge pressure. Often, the second stage is physically smaller than the primary stage, to accommodate the already compressed gas without reducing its pressure. Each stage further compresses the gas and increases its pressure and also temperature (if inter cooling between stages is not used). Types Compressors are similar to pumps: both increase the pressure on a fluid (such as a gas) and both can transport the fluid through a pipe. The main distinction is that the focus of a compressor is to change the density or volume of the fluid, which is mostly only achievable on gases. Gases are compressible, while liquids are relatively incompressible, so compressors are rarely used for liquids. The main action of a pump is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Adiabatic Process
An adiabatic process (''adiabatic'' ) is a type of thermodynamic process that occurs without transferring heat between the thermodynamic system and its Environment (systems), environment. Unlike an isothermal process, an adiabatic process transfers energy to the surroundings only as Work (thermodynamics), work and/or mass flow.. A translation may be founhere. Also a mostly reliabltranslation is to be foundin As a key concept in thermodynamics, the adiabatic process supports the theory that explains the first law of thermodynamics. The opposite term to "adiabatic" is ''diabatic''. Some chemical and physical processes occur too rapidly for energy to enter or leave the system as heat, allowing a convenient "adiabatic approximation".Bailyn, M. (1994), pp. 52–53. For example, the adiabatic flame temperature uses this approximation to calculate the upper limit of fire, flame temperature by assuming combustion loses no heat to its surroundings. In meteorology, adiabatic expansion an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chloroprene
Chloroprene (IUPAC name 2-chlorobuta-1,3-diene) is a chemical compound with the molecular formula CH2=CCl−CH=CH2. Chloroprene is a colorless volatile liquid, almost exclusively used as a monomer for the production of the polymer polychloroprene, better known as neoprene, a type of synthetic rubber. History Although it may have been discovered earlier, chloroprene was largely developed by DuPont during the early 1930s, specifically with the formation of neoprene in mind. The chemists Elmer K. Bolton, Wallace Carothers, Arnold Collins and Ira Williams are generally accredited with its development and commercialisation although the work was based upon that of Julius Arthur Nieuwland, with whom they collaborated. Production Chloroprene is produced in three steps from 1,3-butadiene: (i) chlorination, (ii) isomerization of part of the product stream, and (iii) dehydrochlorination of 3,4-dichlorobut-1-ene. Chlorine adds to 1,3-butadiene to afford a mixture of 3,4-dichlorobut-1-e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lead Poisoning
Lead poisoning, also known as plumbism and saturnism, is a type of metal poisoning caused by lead in the body. Symptoms may include abdominal pain, constipation, headaches, irritability, memory problems, infertility, numbness and paresthesia, tingling in the hands and feet. It causes almost 10% of intellectual disability of otherwise unknown cause and can result in behavioral problems. Some of the effects are permanent. In severe cases, anemia, seizures, coma, or death may occur. Exposure to lead can occur by contaminated air, water, dust, food, or consumer products. Lead poisoning poses a significantly increased risk to children and pets as they are far more likely to ingest lead indirectly by chewing on toys or other objects that are coated in lead paint. Additionally, children absorb greater quantities of lead from ingested sources than adults. Exposure at work is a common cause of lead poisoning in adults with certain occupations at particular risk. Diagnosis is typically b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
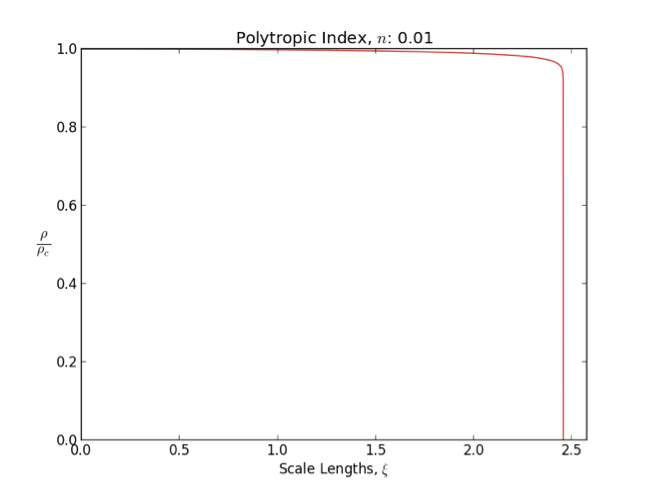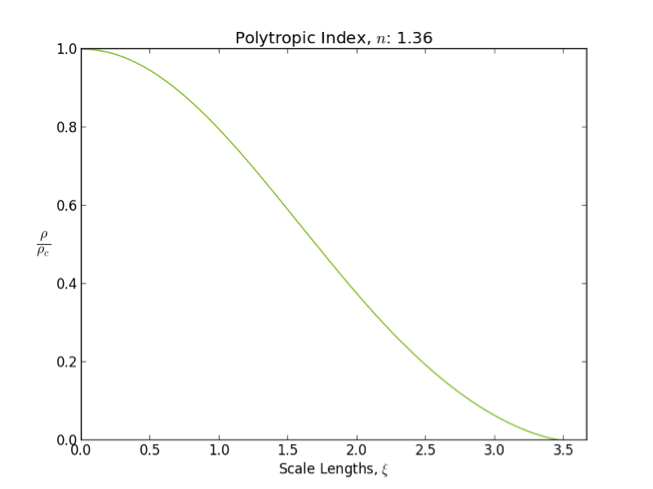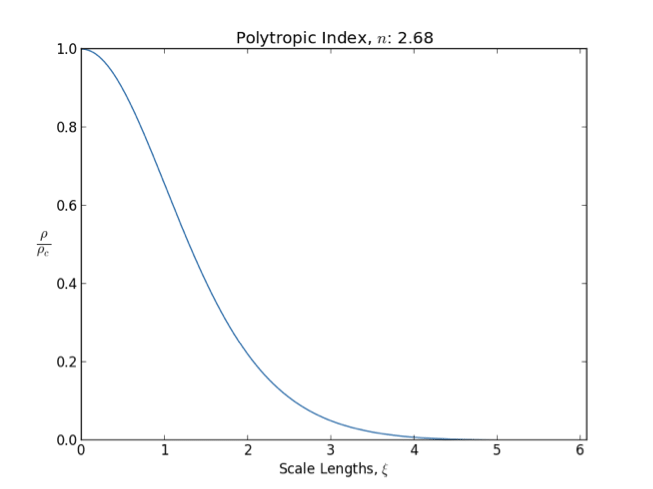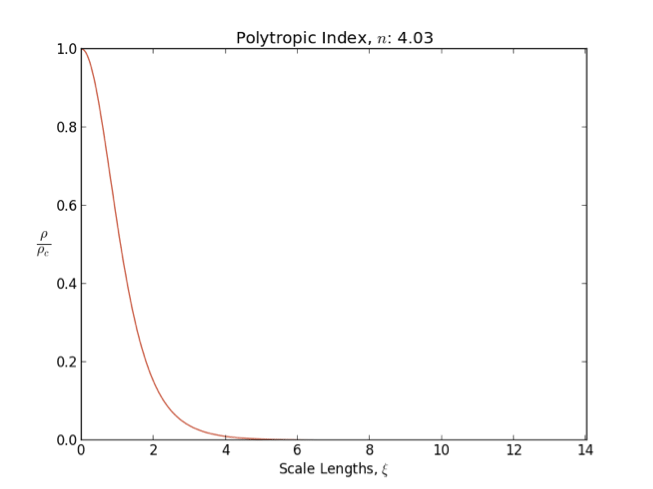
Polytrope
In astrophysics, a polytrope refers to a solution of the Lane–Emden equation in which the pressure depends upon the density in the form P = K \rho^ = K \rho^, where is pressure, is density and is a Constant (mathematics), constant of Proportionality (mathematics), proportionality. The constant is known as the polytropic index; note however that the polytropic index has an alternative definition as with ''n'' as the exponent. This relation need not be interpreted as an equation of state, which states ''P'' as a function of both ρ and ''T'' (the temperature); however in the particular case described by the polytrope equation there are other additional relations between these three quantities, which together determine the equation. Thus, this is simply a relation that expresses an assumption about the change of pressure with radius in terms of the change of density with radius, yielding a solution to the Lane–Emden equation. Sometimes the word ''polytrope'' may refer t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lane–Emden Equation
In astrophysics, the Lane–Emden equation is a dimensionless form of Poisson's equation for the gravitational potential of a Newtonian self-gravitating, spherically symmetric, polytropic fluid. It is named after astrophysicists Jonathan Homer Lane and Robert Emden. The equation reads where \xi is a dimensionless radius and \theta is related to the density, and thus the pressure, by \rho=\rho_c\theta^n for central density \rho_c. The index n is the polytropic index that appears in the polytropic equation of state, P = K \rho^\, where P and \rho are the pressure and density, respectively, and K is a constant of proportionality. The standard boundary conditions are \theta(0)=1 and \theta'(0)=0. Solutions thus describe the run of pressure and density with radius and are known as polytropes of index n. If an isothermal fluid (polytropic index tends to infinity) is used instead of a polytropic fluid, one obtains the Emden–Chandrasekhar equation. Applications Physically, hydro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mayer's Relation
In the 19th century, German chemist and physicist Julius von Mayer derived a relation between the molar heat capacity at constant pressure and the molar heat capacity at constant volume for an ideal gas. Mayer's relation states that C_ - C_ = R, where is the molar heat at constant pressure, is the molar heat at constant volume and is the gas constant. For more general homogeneous substances, not just ideal gases, the difference takes the form, C_ - C_ = V_ T \frac (see relations between heat capacities), where V_ is the molar volume, T is the temperature, \alpha_ is the thermal expansion coefficient and \beta is the isothermal compressibility. From this latter relation, several inferences can be made: * Since the isothermal compressibility \beta_ is positive for nearly all phases, and the square of thermal expansion coefficient \alpha is always either a positive quantity or zero, the specific heat at constant pressure is nearly always greater than or equal to specific heat at ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bounded Function
In mathematics, a function f defined on some set X with real or complex values is called bounded if the set of its values (its image) is bounded. In other words, there exists a real number M such that :, f(x), \le M for all x in X. A function that is ''not'' bounded is said to be unbounded. If f is real-valued and f(x) \leq A for all x in X, then the function is said to be bounded (from) above by A. If f(x) \geq B for all x in X, then the function is said to be bounded (from) below by B. A real-valued function is bounded if and only if it is bounded from above and below. An important special case is a bounded sequence, where ''X'' is taken to be the set \mathbb N of natural numbers. Thus a sequence f = (a_0, a_1, a_2, \ldots) is bounded if there exists a real number M such that :, a_n, \le M for every natural number n. The set of all bounded sequences forms the sequence space l^\infty. The definition of boundedness can be generalized to functions f: X \rightarrow Y taking ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Volume (thermodynamics)
In thermodynamics, the volume of a system is an important extensive parameter for describing its thermodynamic state. The '' specific volume'', an intensive property, is the system's volume per unit mass. Volume is a function of state and is interdependent with other thermodynamic properties such as pressure and temperature. For example, volume is related to the pressure and temperature of an ideal gas by the ideal gas law. The physical region covered by a system may or may not coincide with a ''control volume'' used to analyze the system. Overview The volume of a thermodynamic system typically refers to the volume of the working fluid, such as, for example, the fluid within a piston. Changes to this volume may be made through an application of work, or may be used to produce work. An isochoric process however operates at a constant-volume, thus no work can be produced. Many other thermodynamic processes will result in a change in volume. A polytropic process, in parti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
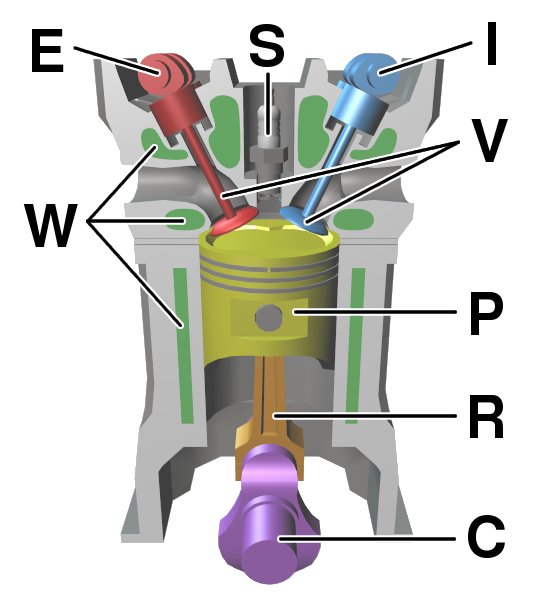
Internal Combustion Engine
An internal combustion engine (ICE or IC engine) is a heat engine in which the combustion of a fuel occurs with an oxidizer (usually air) in a combustion chamber that is an integral part of the working fluid flow circuit. In an internal combustion engine, the expansion of the high-temperature and high-pressure gases produced by combustion applies direct force to some component of the engine. The force is typically applied to pistons (reciprocating engine, piston engine), turbine blades (gas turbine), a Wankel engine, rotor (Wankel engine), or a propulsive nozzle, nozzle (jet engine). This force moves the component over a distance. This process transforms chemical energy into kinetic energy which is used to propel, move or power whatever the engine is attached to. The first commercially successful internal combustion engines were invented in the mid-19th century. The first modern internal combustion engine, the Otto engine, was designed in 1876 by the German engineer Nicolaus ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |