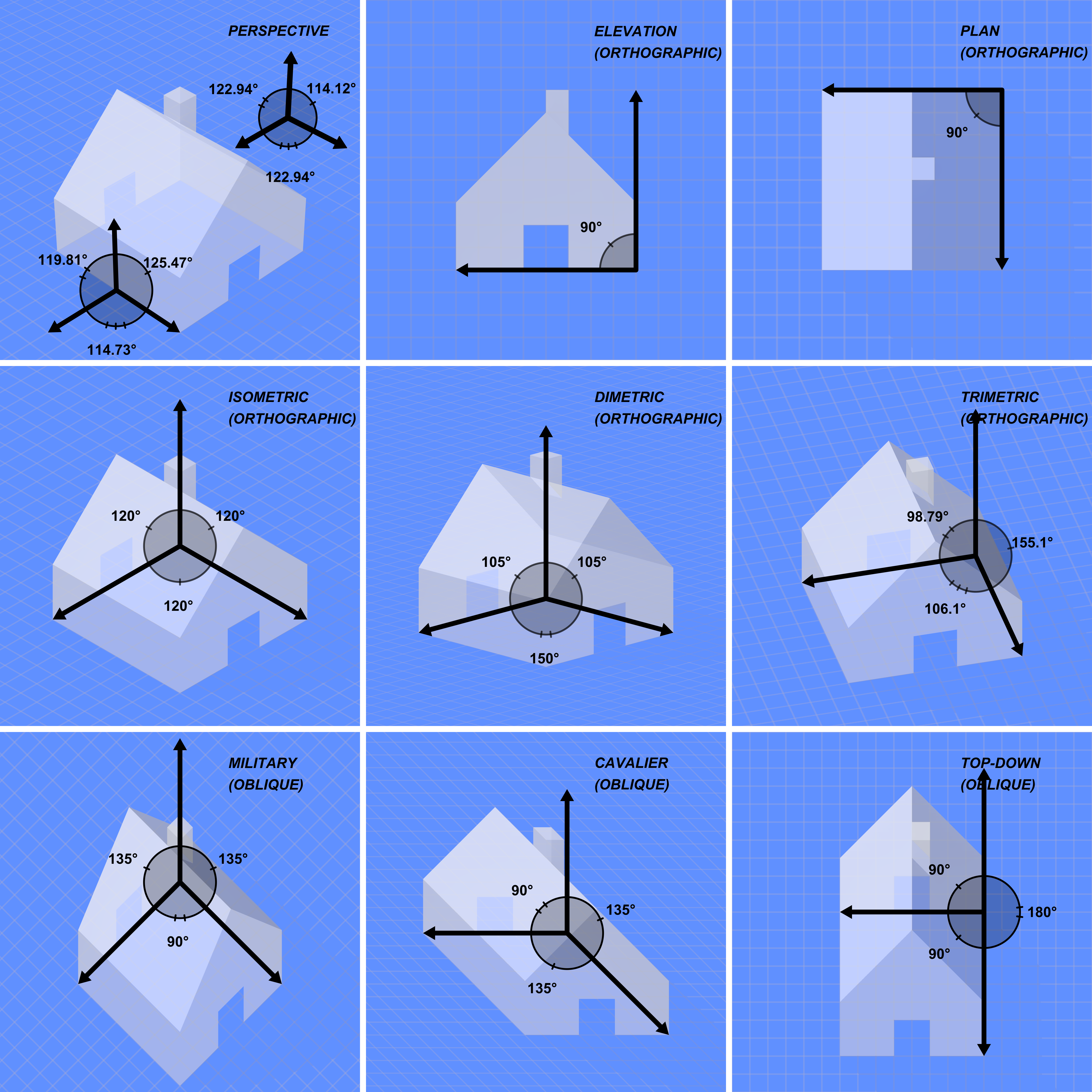
|
Planar Projection
Planar projections are the subset of 3D projection, 3D graphical projections constructed by Linear map, linearly mapping points in three-dimensional space to points on a two-dimensional projection plane. The projected point on the Plane (geometry), plane is chosen such that it is Line (geometry), collinear with the corresponding three-dimensional point and the centre of projection. The lines connecting these points are commonly referred to as projectors. The centre of projection can be thought of as the location of the observer, while the plane of projection is the surface on which the two dimensional projected image of the scene is recorded or from which it is viewed (e.g., photographic negative, photographic print, computer monitor). When the centre of projection is at a finite distance from the projection plane, a Perspective (graphical), perspective projection is obtained. When the centre of projection is at infinity, all the projectors are parallel, and the corresponding su ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
3D Projection
A 3D projection (or graphical projection) is a Design, design technique used to display a three-dimensional (3D) object on a two-dimensional (2D) surface. These projections rely on perspective (graphical), visual perspective and aspect analysis to Projection mapping, project a complex object for viewing capability on a simpler plane. 3D projections use the Primary Qualities, primary qualities of an object's basic shape to create a map of points, that are then connected to one another to create a visual element. The result is a graphic that contains conceptual properties to interpret the figure or image as not actually flat (2D), but rather, as a solid object (3D) being viewed on a 2D display. 3D objects are largely displayed on two-dimensional mediums (such as paper and computer monitors). As such, graphical projections are a commonly used design element; notably, in engineering drawing, technical drawing, drafting, and computer graphics. Projections can be calculated through ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Map
In mathematics, and more specifically in linear algebra, a linear map (also called a linear mapping, linear transformation, vector space homomorphism, or in some contexts linear function) is a mapping V \to W between two vector spaces that preserves the operations of vector addition and scalar multiplication. The same names and the same definition are also used for the more general case of modules over a ring; see Module homomorphism. If a linear map is a bijection then it is called a . In the case where V = W, a linear map is called a linear endomorphism. Sometimes the term refers to this case, but the term "linear operator" can have different meanings for different conventions: for example, it can be used to emphasize that V and W are real vector spaces (not necessarily with V = W), or it can be used to emphasize that V is a function space, which is a common convention in functional analysis. Sometimes the term ''linear function'' has the same meaning as ''linear m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Three-dimensional Space
In geometry, a three-dimensional space (3D space, 3-space or, rarely, tri-dimensional space) is a mathematical space in which three values ('' coordinates'') are required to determine the position of a point. Most commonly, it is the three-dimensional Euclidean space, that is, the Euclidean space of dimension three, which models physical space. More general three-dimensional spaces are called '' 3-manifolds''. The term may also refer colloquially to a subset of space, a ''three-dimensional region'' (or 3D domain), a '' solid figure''. Technically, a tuple of numbers can be understood as the Cartesian coordinates of a location in a -dimensional Euclidean space. The set of these -tuples is commonly denoted \R^n, and can be identified to the pair formed by a -dimensional Euclidean space and a Cartesian coordinate system. When , this space is called the three-dimensional Euclidean space (or simply "Euclidean space" when the context is clear). In classical physics, it serve ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Two-dimensional
A two-dimensional space is a mathematical space with two dimensions, meaning points have two degrees of freedom: their locations can be locally described with two coordinates or they can move in two independent directions. Common two-dimensional spaces are often called '' planes'', or, more generally, '' surfaces''. These include analogs to physical spaces, like flat planes, and curved surfaces like spheres, cylinders, and cones, which can be infinite or finite. Some two-dimensional mathematical spaces are not used to represent physical positions, like an affine plane or complex plane. Flat The most basic example is the flat Euclidean plane, an idealization of a flat surface in physical space such as a sheet of paper or a chalkboard. On the Euclidean plane, any two points can be joined by a unique straight line along which the distance can be measured. The space is flat because any two lines transversed by a third line perpendicular to both of them are parallel, meaning th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Plane (geometry)
In mathematics, a Euclidean plane is a Euclidean space of dimension two, denoted \textbf^2 or \mathbb^2. It is a geometric space in which two real numbers are required to determine the position of each point. It is an affine space, which includes in particular the concept of parallel lines. It has also metrical properties induced by a distance, which allows to define circles, and angle measurement. A Euclidean plane with a chosen Cartesian coordinate system is called a '' Cartesian plane''. The set \mathbb^2 of the ordered pairs of real numbers (the real coordinate plane), equipped with the dot product, is often called ''the'' Euclidean plane or ''standard Euclidean plane'', since every Euclidean plane is isomorphic to it. History Books I through IV and VI of Euclid's Elements dealt with two-dimensional geometry, developing such notions as similarity of shapes, the Pythagorean theorem (Proposition 47), equality of angles and areas, parallelism, the sum of the angles ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Line (geometry)
In geometry, a straight line, usually abbreviated line, is an infinitely long object with no width, depth, or curvature, an idealization of such physical objects as a straightedge, a taut string, or a ray (optics), ray of light. Lines are space (mathematics), spaces of dimension one, which may be Embedding, embedded in spaces of dimension two, three, or higher. The word ''line'' may also refer, in everyday life, to a line segment, which is a part of a line delimited by two Point (geometry), points (its ''endpoints''). Euclid's Elements, Euclid's ''Elements'' defines a straight line as a "breadthless length" that "lies evenly with respect to the points on itself", and introduced several postulates as basic unprovable properties on which the rest of geometry was established. ''Euclidean line'' and ''Euclidean geometry'' are terms introduced to avoid confusion with generalizations introduced since the end of the 19th century, such as Non-Euclidean geometry, non-Euclidean, Project ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Image
An image or picture is a visual representation. An image can be Two-dimensional space, two-dimensional, such as a drawing, painting, or photograph, or Three-dimensional space, three-dimensional, such as a carving or sculpture. Images may be displayed through other media, including a Projector, projection on a surface, activation of electronic signals, or Display device, digital displays; they can also be reproduced through mechanical means, such as photography, printmaking, or Photocopier, photocopying. Images can also be Animation, animated through digital or physical processes. In the context of signal processing, an image is a distributed amplitude of color(s). In optics, the term ''image'' (or ''optical image'') refers specifically to the reproduction of an object formed by light waves coming from the object. A ''volatile image'' exists or is perceived only for a short period. This may be a reflection of an object by a mirror, a projection of a camera obscura, or a scene d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Perspective (graphical)
Linear or point-projection perspective () is one of two types of graphical projection perspective in the graphic arts; the other is parallel projection. Linear perspective is an approximate representation, generally on a flat surface, of an image as it is seen by the eye. Perspective drawing is useful for representing a three-dimensional scene in a two-dimensional medium, like paper. It is based on the optical fact that for a person an object looks N times (linearly) smaller if it has been moved N times further from the eye than the original distance was. The most characteristic features of linear perspective are that objects appear smaller as their distance from the observer increases, and that they are subject to , meaning that an object's dimensions parallel to the line of sight appear shorter than its dimensions perpendicular to the line of sight. All objects will recede to points in the distance, usually along the horizon line, but also above and below the horiz ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Transformations
In mathematics, and more specifically in linear algebra, a linear map (also called a linear mapping, linear transformation, vector space homomorphism, or in some contexts linear function) is a mapping V \to W between two vector spaces that preserves the operations of vector addition and scalar multiplication. The same names and the same definition are also used for the more general case of modules over a ring; see Module homomorphism. If a linear map is a bijection then it is called a . In the case where V = W, a linear map is called a linear endomorphism. Sometimes the term refers to this case, but the term "linear operator" can have different meanings for different conventions: for example, it can be used to emphasize that V and W are real vector spaces (not necessarily with V = W), or it can be used to emphasize that V is a function space, which is a common convention in functional analysis. Sometimes the term ''linear function'' has the same meaning as ''linear map'', ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Function Composition
In mathematics, the composition operator \circ takes two function (mathematics), functions, f and g, and returns a new function h(x) := (g \circ f) (x) = g(f(x)). Thus, the function is function application, applied after applying to . (g \circ f) is pronounced "the composition of and ". Reverse composition, sometimes denoted f \mapsto g , applies the operation in the opposite order, applying f first and g second. Intuitively, reverse composition is a chaining process in which the output of function feeds the input of function . The composition of functions is a special case of the composition of relations, sometimes also denoted by \circ. As a result, all properties of composition of relations are true of composition of functions, such as #Properties, associativity. Examples * Composition of functions on a finite set (mathematics), set: If , and , then , as shown in the figure. * Composition of functions on an infinite set: If (where is the set of all real numbers) is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orthographic Projection
Orthographic projection (also orthogonal projection and analemma) is a means of representing Three-dimensional space, three-dimensional objects in Plane (mathematics), two dimensions. Orthographic projection is a form of parallel projection in which all the projection lines are orthogonal to the projection plane, resulting in every plane of the scene appearing in affine transformation on the viewing surface. The obverse of an orthographic projection is an oblique projection, which is a parallel projection in which the projection lines are ''not'' orthogonal to the projection plane. The term ''orthographic'' sometimes means a technique in multiview projection in which principal axes or the planes of the subject are also parallel with the projection plane to create the ''primary views''. If the principal planes or axes of an object in an orthographic projection are ''not'' parallel with the projection plane, the depiction is called ''axonometric'' or an ''auxiliary views''. (''Ax ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rotation (mathematics)
Rotation in mathematics is a concept originating in geometry. Any rotation is a motion of a certain space that preserves at least one point. It can describe, for example, the motion of a rigid body around a fixed point. Rotation can have a sign (as in the sign of an angle): a clockwise rotation is a negative magnitude so a counterclockwise turn has a positive magnitude. A rotation is different from other types of motions: translations, which have no fixed points, and (hyperplane) reflections, each of them having an entire -dimensional flat of fixed points in a - dimensional space. Mathematically, a rotation is a map. All rotations about a fixed point form a group under composition called the rotation group (of a particular space). But in mechanics and, more generally, in physics, this concept is frequently understood as a coordinate transformation (importantly, a transformation of an orthonormal basis), because for any motion of a body there is an inverse transformat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |