|
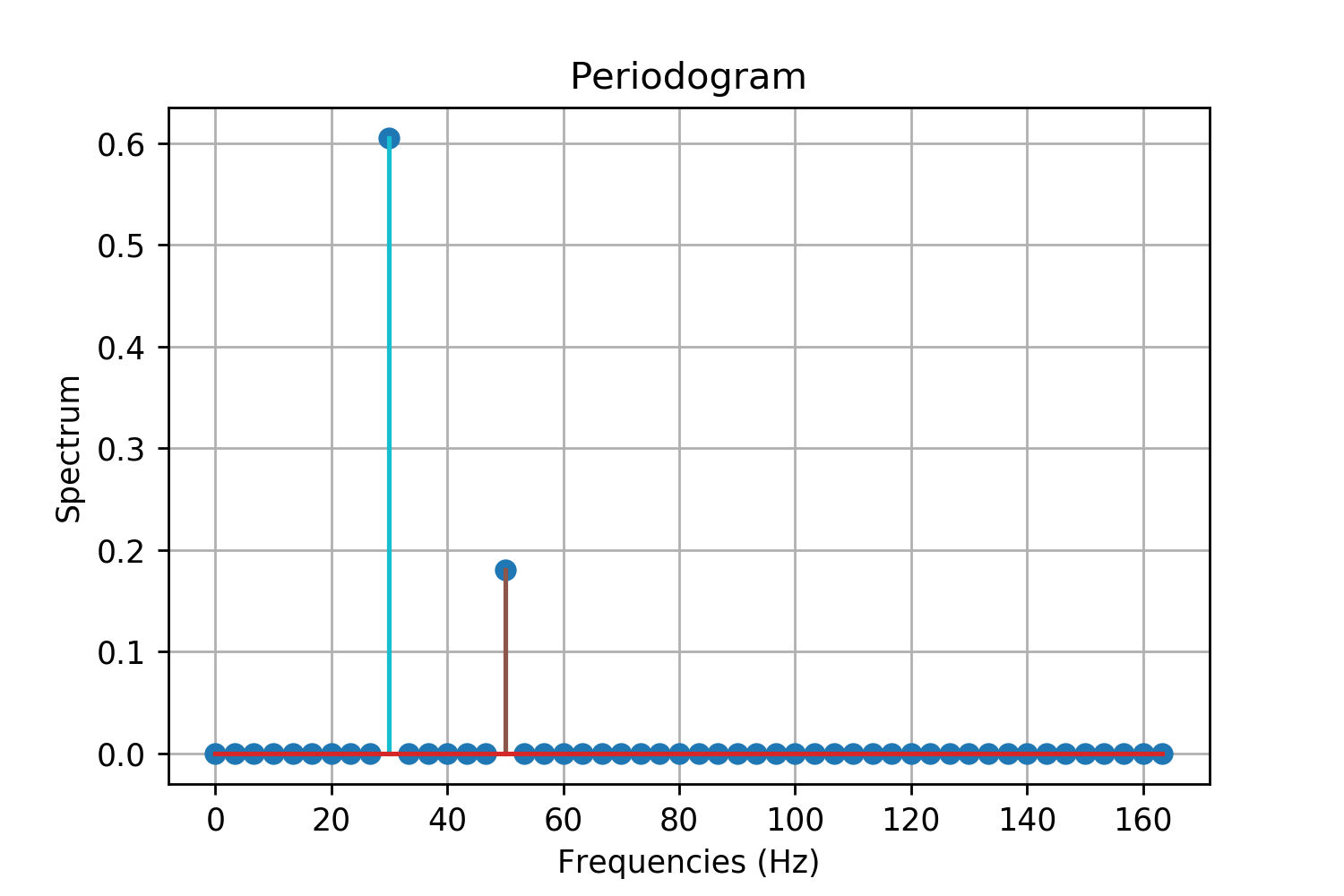
Periodogram
In signal processing, a periodogram is an estimate of the spectral density of a signal. The term was coined by Arthur Schuster in 1898. Today, the periodogram is a component of more sophisticated methods (see spectral estimation). It is the most common tool for examining the amplitude vs frequency characteristics of FIR filters and window functions. FFT spectrum analyzers are also implemented as a time-sequence of periodograms. Definition There are at least two different definitions in use today. One of them involves time-averaging, and one does not. Time-averaging is also the purview of other articles (Bartlett's method and Welch's method). This article is not about time-averaging. The definition of interest here is that the power spectral density of a continuous function, x(t), is the Fourier transform of its auto-correlation function (see Cross-correlation theorem, Spectral density#Power spectral density, and Wiener–Khinchin theorem): :\mathcal\ = X(f)\cdot X^ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Least-squares Spectral Analysis
Least-squares spectral analysis (LSSA) is a method of estimating a frequency spectrum, based on a least squares fit of sinusoids to data samples, similar to Fourier analysis. Fourier analysis, the most used spectral method in science, generally boosts long-periodic noise in long gapped records; LSSA mitigates such problems. Unlike with Fourier analysis, data need not be equally spaced to use LSSA. LSSA is also known as the Vaníček method or the Gauss-Vaniček method after Petr Vaníček, and as the Lomb method or the Lomb–Scargle periodogram, based on the contributions of Nicholas R. Lomb and, independently, Jeffrey D. Scargle. Historical background The close connections between Fourier analysis, the periodogram, and least-squares fitting of sinusoids have long been known. Most developments, however, are restricted to complete data sets of equally spaced samples. In 1963, Freek J. M. Barning of Mathematisch Centrum, Amsterdam, handled unequally spaced data by similar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
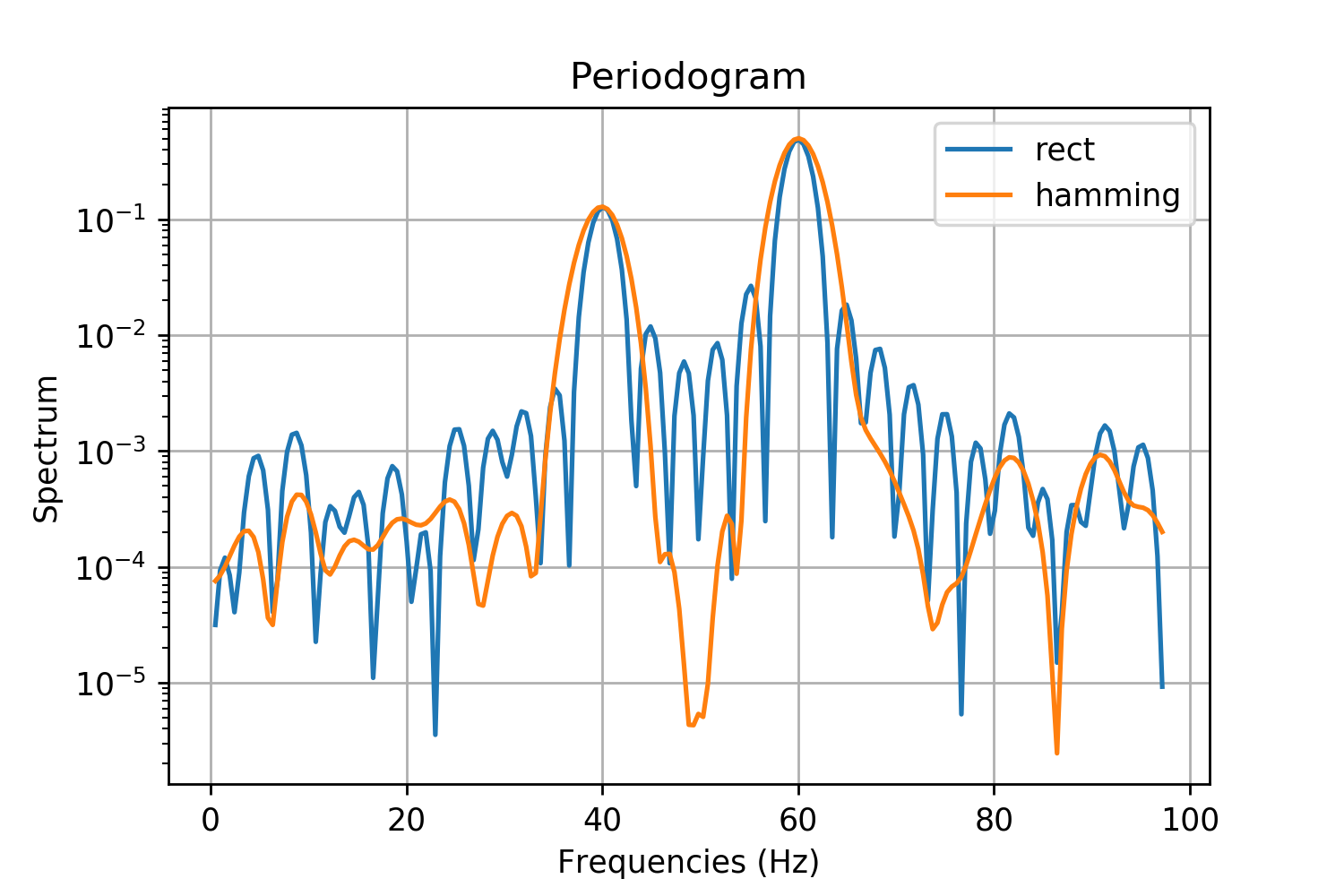
Periodogram Windows
In signal processing, a periodogram is an estimate of the spectral density of a signal. The term was coined by Arthur Schuster in 1898. Today, the periodogram is a component of more sophisticated methods (see spectral estimation). It is the most common tool for examining the amplitude vs frequency characteristics of FIR filters and window functions. FFT spectrum analyzers are also implemented as a time-sequence of periodograms. Definition There are at least two different definitions in use today. One of them involves time-averaging, and one does not. Time-averaging is also the purview of other articles ( Bartlett's method and Welch's method). This article is not about time-averaging. The definition of interest here is that the power spectral density of a continuous function, x(t), is the Fourier transform of its auto-correlation function (see Cross-correlation theorem, Spectral density#Power spectral density, and Wiener–Khinchin theorem): :\mathcal\ = X(f)\cdot X^* ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Periodogram
In signal processing, a periodogram is an estimate of the spectral density of a signal. The term was coined by Arthur Schuster in 1898. Today, the periodogram is a component of more sophisticated methods (see spectral estimation). It is the most common tool for examining the amplitude vs frequency characteristics of FIR filters and window functions. FFT spectrum analyzers are also implemented as a time-sequence of periodograms. Definition There are at least two different definitions in use today. One of them involves time-averaging, and one does not. Time-averaging is also the purview of other articles (Bartlett's method and Welch's method). This article is not about time-averaging. The definition of interest here is that the power spectral density of a continuous function, x(t), is the Fourier transform of its auto-correlation function (see Cross-correlation theorem, Spectral density#Power spectral density, and Wiener–Khinchin theorem): :\mathcal\ = X(f)\cdot X^ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spectral Estimation
In statistical signal processing, the goal of spectral density estimation (SDE) or simply spectral estimation is to estimate the spectral density (also known as the power spectral density) of a signal from a sequence of time samples of the signal. Intuitively speaking, the spectral density characterizes the frequency content of the signal. One purpose of estimating the spectral density is to detect any periodicities in the data, by observing peaks at the frequencies corresponding to these periodicities. Some SDE techniques assume that a signal is composed of a limited (usually small) number of generating frequencies plus noise and seek to find the location and intensity of the generated frequencies. Others make no assumption on the number of components and seek to estimate the whole generating spectrum. Overview Spectrum analysis, also referred to as frequency domain analysis or spectral density estimation, is the technical process of decomposing a complex signal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spectral Density Estimation
In statistical signal processing, the goal of spectral density estimation (SDE) or simply spectral estimation is to estimate the spectral density (also known as the power spectral density) of a signal from a sequence of time samples of the signal. Intuitively speaking, the spectral density characterizes the frequency content of the signal. One purpose of estimating the spectral density is to detect any periodicities in the data, by observing peaks at the frequencies corresponding to these periodicities. Some SDE techniques assume that a signal is composed of a limited (usually small) number of generating frequencies plus noise and seek to find the location and intensity of the generated frequencies. Others make no assumption on the number of components and seek to estimate the whole generating spectrum. Overview Spectrum analysis, also referred to as frequency domain analysis or spectral density estimation, is the technical process of decomposing a complex signal in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bartlett's Method
In time series analysis, Bartlett's method (also known as the method of averaged periodograms), is used for estimating power spectra. It provides a way to reduce the variance of the periodogram in exchange for a reduction of resolution, compared to standard periodograms. A final estimate of the spectrum at a given frequency is obtained by averaging the estimates from the periodograms (at the same frequency) derived from non-overlapping portions of the original series. The method is used in physics, engineering, and applied mathematics. Common applications of Bartlett's method are frequency response measurements and general spectrum analysis. The method is named after M. S. Bartlett who first proposed it. Definition and procedure Bartlett’s method consists of the following steps: # The original N point data segment is split up into K (non-overlapping) data segments, each of length M # For each segment, compute the periodogram by computing the discrete Fourier transform (DFT v ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Welch's Method
Welch's method, named after Peter D. Welch, is an approach for spectral density estimation. It is used in physics, engineering, and applied mathematics for estimating the power of a signal at different frequencies. The method is based on the concept of using periodogram spectrum estimates, which are the result of converting a signal from the time domain to the frequency domain. Welch's method is an improvement on the standard periodogram spectrum estimating method and on Bartlett's method, in that it reduces noise in the estimated power spectra in exchange for reducing the frequency resolution. Due to the noise caused by imperfect and finite data, the noise reduction from Welch's method is often desired. Definition and procedure The Welch method is based on Bartlett's method and differs in two ways: # The signal is split up into overlapping segments: the original data segment is split up into L data segments of length M, overlapping by D points. ## If D = M / 2, the overlap is s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spectral Density
The power spectrum S_(f) of a time series x(t) describes the distribution of power into frequency components composing that signal. According to Fourier analysis, any physical signal can be decomposed into a number of discrete frequencies, or a spectrum of frequencies over a continuous range. The statistical average of a certain signal or sort of signal (including noise) as analyzed in terms of its frequency content, is called its spectrum. When the energy of the signal is concentrated around a finite time interval, especially if its total energy is finite, one may compute the energy spectral density. More commonly used is the power spectral density (or simply power spectrum), which applies to signals existing over ''all'' time, or over a time period large enough (especially in relation to the duration of a measurement) that it could as well have been over an infinite time interval. The power spectral density (PSD) then refers to the spectral energy distribution that would ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Discrete-time Fourier Transform
In mathematics, the discrete-time Fourier transform (DTFT) is a form of Fourier analysis that is applicable to a sequence of values. The DTFT is often used to analyze samples of a continuous function. The term ''discrete-time'' refers to the fact that the transform operates on discrete data, often samples whose interval has units of time. From uniformly spaced samples it produces a function of frequency that is a periodic summation of the continuous Fourier transform of the original continuous function. Under certain theoretical conditions, described by the sampling theorem, the original continuous function can be recovered perfectly from the DTFT and thus from the original discrete samples. The DTFT itself is a continuous function of frequency, but discrete samples of it can be readily calculated via the discrete Fourier transform (DFT) (see ), which is by far the most common method of modern Fourier analysis. Both transforms are invertible. The inverse DTFT is the ori ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Arthur Schuster
Sir Franz Arthur Friedrich Schuster (12 September 1851 – 14 October 1934) was a German-born British physicist known for his work in spectroscopy, electrochemistry, optics, X-radiography and the application of harmonic analysis to physics. Schuster's integral is named after him. He contributed to making the University of Manchester a centre for the study of physics. Early years Arthur Schuster was born in Frankfurt am Main, Germany the son of Francis Joseph Schuster, a cotton merchant and banker, and his wife Marie Pfeiffer. Schuster's parents were married in 1849, converted from Judaism to Christianity, and brought up their children in that faith. In 1869, his father moved to Manchester where the family textile business was based. Arthur, who had been to school in Frankfurt and was studying in Geneva, joined his parents in 1870 and he and the other children became British citizens in 1875. Edgar Schuster (1897–1969) was his nephew. From his childhood, Schuster had bee ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |