|
Perfect Gas
In physics, engineering, and physical chemistry, a perfect gas is a theoretical gas model that differs from real gases in specific ways that makes certain calculations easier to handle. In all perfect gas models, intermolecular forces are neglected. This means that one can neglect many complications that may arise from the Van der Waals forces. All perfect gas models are ideal gas models in the sense that they all follow the ideal gas equation of state. However, the idea of a perfect gas model is often invoked as a combination of the ideal gas equation of state with specific additional assumptions regarding the variation (or nonvariation) of the heat capacity with temperature. Perfect gas nomenclature The terms ''perfect gas'' and ''ideal gas'' are sometimes used interchangeably, depending on the particular field of physics and engineering. Sometimes, other distinctions are made, such as between ''thermally perfect gas'' and ''calorically perfect gas'', or between imperfect, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Physics
Physics is the scientific study of matter, its Elementary particle, fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge which relates to the order of nature, or, in other words, to the regular succession of events." It is one of the most fundamental scientific disciplines. "Physics is one of the most fundamental of the sciences. Scientists of all disciplines use the ideas of physics, including chemists who study the structure of molecules, paleontologists who try to reconstruct how dinosaurs walked, and climatologists who study how human activities affect the atmosphere and oceans. Physics is also the foundation of all engineering and technology. No engineer could design a flat-screen TV, an interplanetary spacecraft, or even a better mousetrap without first understanding the basic laws of physics. (...) You will come to see physics as a towering achievement of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
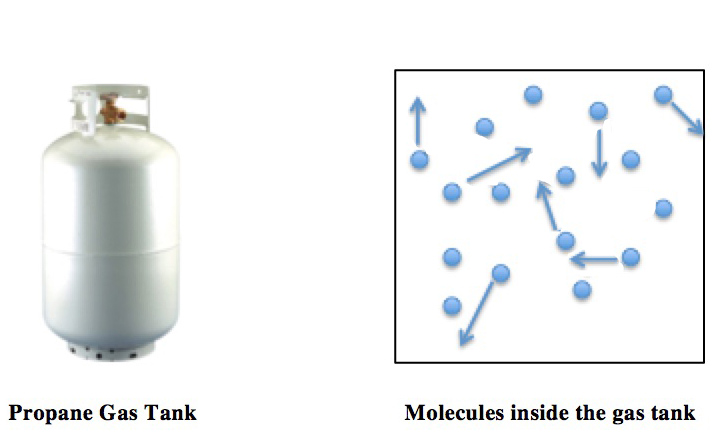
Ideal Gas
An ideal gas is a theoretical gas composed of many randomly moving point particles that are not subject to interparticle interactions. The ideal gas concept is useful because it obeys the ideal gas law, a simplified equation of state, and is amenable to analysis under statistical mechanics. The requirement of zero interaction can often be relaxed if, for example, the interaction is perfectly elastic or regarded as point-like collisions. Under various conditions of temperature and pressure, many real gases behave qualitatively like an ideal gas where the gas molecules (or atoms for monatomic gas) play the role of the ideal particles. Many gases such as nitrogen, oxygen, hydrogen, noble gases, some heavier gases like carbon dioxide and mixtures such as air, can be treated as ideal gases within reasonable tolerances over a considerable parameter range around standard temperature and pressure. Generally, a gas behaves more like an ideal gas at higher temperature and lower ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ideal Gas Law
The ideal gas law, also called the general gas equation, is the equation of state of a hypothetical ideal gas. It is a good approximation of the behavior of many gases under many conditions, although it has several limitations. It was first stated by Benoît Paul Émile Clapeyron in 1834 as a combination of the empirical Boyle's law, Charles's law, Avogadro's law, and Gay-Lussac's law. The ideal gas law is often written in an empirical form: pV = nRT where p, V and T are the pressure, volume and Thermodynamic temperature, temperature respectively; n is the amount of substance; and R is the ideal gas constant. It can also be derived from the microscopic kinetic theory of gases, kinetic theory, as was achieved (independently) by August Krönig in 1856 and Rudolf Clausius in 1857. Equation The state function, state of an amount of gas is determined by its pressure, volume, and temperature. The modern form of the equation relates these simply in two main forms. The temperature us ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gas Laws
The laws describing the behaviour of gases under fixed pressure, volume, amount of gas, and absolute temperature conditions are called gas laws. The basic gas laws were discovered by the end of the 18th century when scientists found out that relationships between pressure, volume and temperature of a sample of gas could be obtained which would hold to approximation for all gases. The combination of several empirical gas laws led to the development of the ideal gas law. The ideal gas law was later found to be consistent with atomic and kinetic theory. History In 1643, the Italian physicist and mathematician, Evangelista Torricelli, who for a few months had acted as Galileo Galilei's secretary, conducted a celebrated experiment in Florence. He demonstrated that a column of mercury in an inverted tube can be supported by the pressure of air outside of the tube, with the creation of a small section of vacuum above the mercury. This experiment essentially paved the way towards ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Axial Compressor
An axial compressor is a gas compressor that can continuously pressurize gases. It is a rotating, airfoil-based compressor in which the gas or working fluid principally flows parallel to the axis of rotation, or axially. This differs from other rotating compressors such as centrifugal compressor, axi-centrifugal compressors and mixed-flow compressors where the fluid flow will include a "radial component" through the compressor. The energy level of the fluid increases as it flows through the compressor due to the action of the rotor blades which exert a torque on the fluid. The stationary blades slow the fluid, converting the circumferential component of flow into pressure. Compressors are typically driven by an electric motor or a steam or a gas turbine. Axial flow compressors produce a continuous flow of compressed gas, and have the benefits of high efficiency and large mass flow rate, particularly in relation to their size and cross-section. They do, however, require several ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Boltzmann Distribution
In statistical mechanics and mathematics, a Boltzmann distribution (also called Gibbs distribution Translated by J.B. Sykes and M.J. Kearsley. See section 28) is a probability distribution or probability measure that gives the probability that a system will be in a certain state as a function of that state's energy and the temperature of the system. The distribution is expressed in the form: :p_i \propto \exp\left(- \frac \right) where is the probability of the system being in state , is the exponential function, is the energy of that state, and a constant of the distribution is the product of the Boltzmann constant and thermodynamic temperature . The symbol \propto denotes proportionality (see for the proportionality constant). The term ''system'' here has a wide meaning; it can range from a collection of 'sufficient number' of atoms or a single atom to a macroscopic system such as a natural gas storage tank. Therefore, the Boltzmann distribution can be used to sol ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Statistical Mechanics
Quantum statistical mechanics is statistical mechanics applied to quantum mechanical systems. It relies on constructing density matrices that describe quantum systems in thermal equilibrium. Its applications include the study of collections of identical particles, which provides a theory that explains phenomena including superconductivity and superfluidity. Density matrices, expectation values, and entropy In quantum mechanics, probabilities for the outcomes of experiments made upon a system are calculated from the quantum state describing that system. Each physical system is associated with a vector space, or more specifically a Hilbert space. The dimension of the Hilbert space may be infinite, as it is for the space of square-integrable functions on a line, which is used to define the quantum physics of a continuous degree of freedom. Alternatively, the Hilbert space may be finite-dimensional, as occurs for spin degrees of freedom. A density operator, the mathematical r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Equipartition Theorem
In classical physics, classical statistical mechanics, the equipartition theorem relates the temperature of a system to its average energy, energies. The equipartition theorem is also known as the law of equipartition, equipartition of energy, or simply equipartition. The original idea of equipartition was that, in thermal equilibrium, energy is shared equally among all of its various forms; for example, the average kinetic energy per Degrees of freedom (physics and chemistry), degree of freedom in translation (physics), translational motion of a molecule should equal that in rotational motion. The equipartition theorem makes quantitative predictions. Like the virial theorem, it gives the total average kinetic and potential energies for a system at a given temperature, from which the system's heat capacity can be computed. However, equipartition also gives the average values of individual components of the energy, such as the kinetic energy of a particular particle or the potent ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kinetic Theory Of Gases
The kinetic theory of gases is a simple classical model of the thermodynamic behavior of gases. Its introduction allowed many principal concepts of thermodynamics to be established. It treats a gas as composed of numerous particles, too small to be seen with a microscope, in constant, random motion. These particles are now known to be the atoms or molecules of the gas. The kinetic theory of gases uses their collisions with each other and with the walls of their container to explain the relationship between the macroscopic properties of gases, such as volume, pressure, and temperature, as well as transport properties such as viscosity, thermal conductivity and mass diffusivity. The basic version of the model describes an ideal gas. It treats the collisions as perfectly elastic and as the only interaction between the particles, which are additionally assumed to be much smaller than their average distance apart. Due to the time reversibility of microscopic dynamics ( microsco ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistical Mechanics
In physics, statistical mechanics is a mathematical framework that applies statistical methods and probability theory to large assemblies of microscopic entities. Sometimes called statistical physics or statistical thermodynamics, its applications include many problems in a wide variety of fields such as biology, neuroscience, computer science Computer science is the study of computation, information, and automation. Computer science spans Theoretical computer science, theoretical disciplines (such as algorithms, theory of computation, and information theory) to Applied science, ..., information theory and sociology. Its main purpose is to clarify the properties of matter in aggregate, in terms of physical laws governing atomic motion. Statistical mechanics arose out of the development of classical thermodynamics, a field for which it was successful in explaining macroscopic physical properties—such as temperature, pressure, and heat capacity—in terms of microscop ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Thermodynamic Equations
Thermodynamics is expressed by a mathematical framework of ''thermodynamic equations'' which relate various thermodynamic quantities and physical properties measured in a laboratory or production process. Thermodynamics is based on a fundamental set of postulates, that became the laws of thermodynamics. Introduction One of the fundamental thermodynamic equations is the description of thermodynamic work in analogy to mechanical work, or weight lifted through an elevation against gravity, as defined in 1824 by French physicist Sadi Carnot. Carnot used the phrase motive power for work. In the footnotes to his famous ''On the Motive Power of Fire'', he states: “We use here the expression ''motive power'' to express the useful effect that a motor is capable of producing. This effect can always be likened to the elevation of a weight to a certain height. It has, as we know, as a measure, the product of the weight multiplied by the height to which it is raised.” With the in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Differential (mathematics)
In mathematics, differential refers to several related notions derived from the early days of calculus, put on a rigorous footing, such as infinitesimal differences and the derivatives of functions. The term is used in various branches of mathematics such as calculus, differential geometry, algebraic geometry and algebraic topology. Introduction The term differential is used nonrigorously in calculus to refer to an infinitesimal ("infinitely small") change in some varying quantity. For example, if ''x'' is a variable, then a change in the value of ''x'' is often denoted Δ''x'' (pronounced ''delta x''). The differential ''dx'' represents an infinitely small change in the variable ''x''. The idea of an infinitely small or infinitely slow change is, intuitively, extremely useful, and there are a number of ways to make the notion mathematically precise. Using calculus, it is possible to relate the infinitely small changes of various variables to each other mathematically us ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |