|
Percentiles
In statistics, a ''k''-th percentile (percentile score or centile) is a score ''below which'' a given percentage ''k'' of scores in its frequency distribution falls (exclusive definition) or a score ''at or below which'' a given percentage falls (inclusive definition). For example, the 50th percentile (the median) is the score below which 50% of the scores in the distribution are found (by the "exclusive" definition), or at or below which 50% of the scores are found (by the "inclusive" definition). Percentiles are expressed in the same unit of measurement as the input scores; for example, if the scores refer to human weight, the corresponding percentiles will be expressed in kilograms or pounds. The percentile score and the ''percentile rank'' are related terms. The percentile rank of a score is the percentage of scores in its distribution that are less than it, an exclusive definition, and one that can be expressed with a single, simple formula. Percentile scores and percent ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Percentile
In statistics, a ''k''-th percentile (percentile score or centile) is a score ''below which'' a given percentage ''k'' of scores in its frequency distribution falls (exclusive definition) or a score ''at or below which'' a given percentage falls (inclusive definition). For example, the 50th percentile (the median) is the score below which 50% of the scores in the distribution are found (by the "exclusive" definition), or at or below which 50% of the scores are found (by the "inclusive" definition). Percentiles are expressed in the same unit of measurement as the input scores; for example, if the scores refer to human weight, the corresponding percentiles will be expressed in kilograms or pounds. The percentile score and the ''percentile rank'' are related terms. The percentile rank of a score is the percentage of scores in its distribution that are less than it, an exclusive definition, and one that can be expressed with a single, simple formula. Percentile scores and percen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Growth Chart
A growth chart is used by pediatricians and other health care providers to follow a child's growth over time. Growth charts have been constructed by observing the growth of large numbers of healthy children over time. The height, weight, and head circumference of a child can be compared to the expected parameters of children of the same age and sex to determine whether the child is growing appropriately. Growth charts can also be used to predict the expected adult height and weight of a child because, in general, children maintain a fairly constant growth curve. When a child deviates from his or her previously established growth curve, investigation into the cause is generally warranted. Parameters used to analyze growth charts include weight velocity (defined as rate of change in weight over time), height velocity (defined as rate of change in stature over time), and whether someone's growth chart crosses percentiles. For instance, endocrine disorders can be associated with a decrea ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ordinal Scale
Ordinal data is a categorical, statistical data type where the variables have natural, ordered categories and the distances between the categories are not known. These data exist on an ordinal scale, one of four levels of measurement described by S. S. Stevens in 1946. The ordinal scale is distinguished from the nominal scale by having a ''ranking''. It also differs from the interval scale and ratio scale by not having category widths that represent equal increments of the underlying attribute. Examples of ordinal data A well-known example of ordinal data is the Likert scale. An example of a Likert scale is: Examples of ordinal data are often found in questionnaires: for example, the survey question "Is your general health poor, reasonable, good, or excellent?" may have those answers coded respectively as 1, 2, 3, and 4. Sometimes data on an interval scale or ratio scale are grouped onto an ordinal scale: for example, individuals whose income is known might be grouped into ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Percentile Rank
In statistics, the percentile rank (PR) of a given score is the percentage of scores in its frequency distribution that are less than that score. Its mathematical formula is : PR = \frac \times 100, where ''CF''—the cumulative frequency—is the count of all scores less than or equal to the score of interest, ''F'' is the frequency for the score of interest, and ''N'' is the number of scores in the distribution. Alternatively, if ''CF'' is the count of all scores less than the score of interest, then : PR = \frac \times 100. The figure illustrates the percentile rank computation and shows how the 0.5 × ''F'' term in the formula ensures that the percentile rank reflects a percentage of scores less than the specified score. For example, for the 10 scores shown in the figure, 60% of them are below a score of 4 (five less than 4 and half of the two equal to 4) and 95% are below 7 (nine less than 7 and half of the one equal to 7). Occasionally the percentile rank of a score is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Normal Distribution
In statistics, a normal distribution or Gaussian distribution is a type of continuous probability distribution for a real-valued random variable. The general form of its probability density function is : f(x) = \frac e^ The parameter \mu is the mean or expectation of the distribution (and also its median and mode), while the parameter \sigma is its standard deviation. The variance of the distribution is \sigma^2. A random variable with a Gaussian distribution is said to be normally distributed, and is called a normal deviate. Normal distributions are important in statistics and are often used in the natural and social sciences to represent real-valued random variables whose distributions are not known. Their importance is partly due to the central limit theorem. It states that, under some conditions, the average of many samples (observations) of a random variable with finite mean and variance is itself a random variable—whose distribution converges to a normal dist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Norm-referenced Test
A norm-referenced test (NRT) is a type of test, assessment, or evaluation which yields an estimate of the position of the tested individual in a predefined population, with respect to the trait being measured. Assigning scores on such tests may be described as relative grading, marking on a curve (BrE) or grading on a curve ( AmE, CanE) (also referred to as curved grading, bell curving, or using grading curves). It is a method of assigning grades to the students in a class in such a way as to obtain or approach a pre-specified distribution of these grades having a specific mean and derivation properties, such as a normal distribution (also called Gaussian distribution). The term "curve" refers to the bell curve, the graphical representation of the probability density of the normal distribution, but this method can be used to achieve any desired distribution of the grades – for example, a uniform distribution. The estimate is derived from the analysis of test scores and possibly ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cumulative Distribution Function
In probability theory and statistics, the cumulative distribution function (CDF) of a real-valued random variable X, or just distribution function of X, evaluated at x, is the probability that X will take a value less than or equal to x. Every probability distribution supported on the real numbers, discrete or "mixed" as well as continuous, is uniquely identified by an ''upwards continuous'' ''monotonic increasing'' cumulative distribution function F : \mathbb R \rightarrow ,1/math> satisfying \lim_F(x)=0 and \lim_F(x)=1. In the case of a scalar continuous distribution, it gives the area under the probability density function from minus infinity to x. Cumulative distribution functions are also used to specify the distribution of multivariate random variables. Definition The cumulative distribution function of a real-valued random variable X is the function given by where the right-hand side represents the probability that the random variable X takes on a value less ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Glivenko–Cantelli Theorem
In the theory of probability, the Glivenko–Cantelli theorem (sometimes referred to as the Fundamental Theorem of Statistics), named after Valery Ivanovich Glivenko and Francesco Paolo Cantelli, determines the asymptotic behaviour of the empirical distribution function as the number of independent and identically distributed observations grows. The uniform convergence of more general empirical measures becomes an important property of the Glivenko–Cantelli classes of functions or sets. The Glivenko–Cantelli classes arise in Vapnik–Chervonenkis theory, with applications to machine learning. Applications can be found in econometrics making use of M-estimators. Statement Assume that X_1,X_2,\dots are independent and identically distributed random variables in \mathbb with common cumulative distribution function F(x). The ''empirical distribution function'' for X_1,\dots,X_n is defined by :F_n(x)=\frac\sum_^n I_(x) = \frac\left, \left\\ where I_C is the indicator fun ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
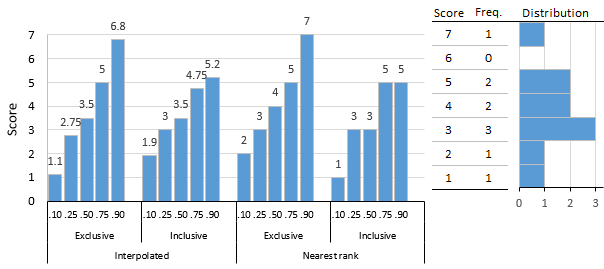
Frequency Histogram And Exclusive And Inclusive Percentiles 2
Frequency is the number of occurrences of a repeating event per unit of time. It is also occasionally referred to as ''temporal frequency'' for clarity, and is distinct from ''angular frequency''. Frequency is measured in hertz (Hz) which is equal to one event per second. The period is the interval of time between events, so the period is the reciprocal of the frequency. For example, if a heart beats at a frequency of 120 times a minute (2 hertz), the period, —the interval at which the beats repeat—is half a second (60 seconds divided by 120 beats). Frequency is an important parameter used in science and engineering to specify the rate of oscillatory and vibratory phenomena, such as mechanical vibrations, audio signals (sound), radio waves, and light. Definitions and units For cyclical phenomena such as oscillations, waves, or for examples of simple harmonic motion, the term ''frequency'' is defined as the number of cycles or vibrations per unit of time. The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistics
Statistics (from German: '' Statistik'', "description of a state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of surveys and experiments.Dodge, Y. (2006) ''The Oxford Dictionary of Statistical Terms'', Oxford University Press. When census data cannot be collected, statisticians collect data by developing specific experiment designs and survey samples. Representative sampling assures that inferences and conclusions can reasonably extend from the sample to the population as a whole. An ex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ranking
A ranking is a relationship between a set of items such that, for any two items, the first is either "ranked higher than", "ranked lower than" or "ranked equal to" the second. In mathematics, this is known as a weak order or total preorder of objects. It is not necessarily a total order of objects because two different objects can have the same ranking. The rankings themselves are totally ordered. For example, materials are totally preordered by hardness, while degrees of hardness are totally ordered. If two items are the same in rank it is considered a tie. By reducing detailed measures to a sequence of ordinal numbers, rankings make it possible to evaluate complex information according to certain criteria. Thus, for example, an Internet search engine may rank the pages it finds according to an estimation of their relevance, making it possible for the user quickly to select the pages they are likely to want to see. Analysis of data obtained by ranking commonly requires no ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
.jpg)
.jpg)



