|
Partial Least Squares Path Modeling
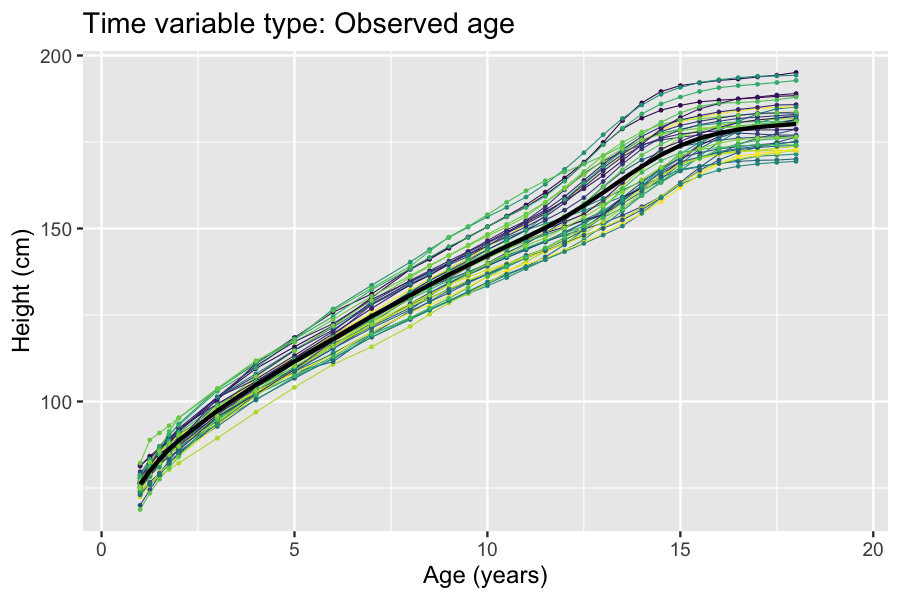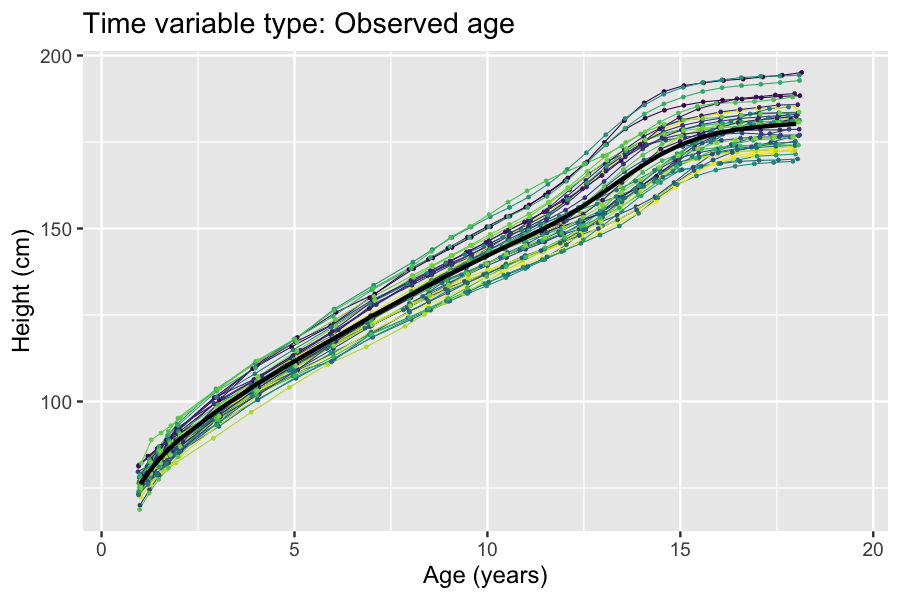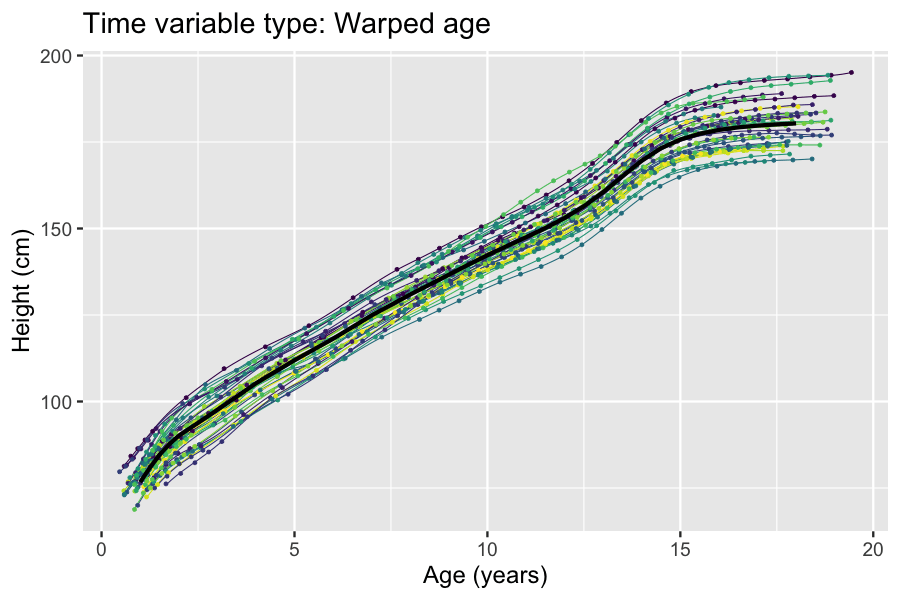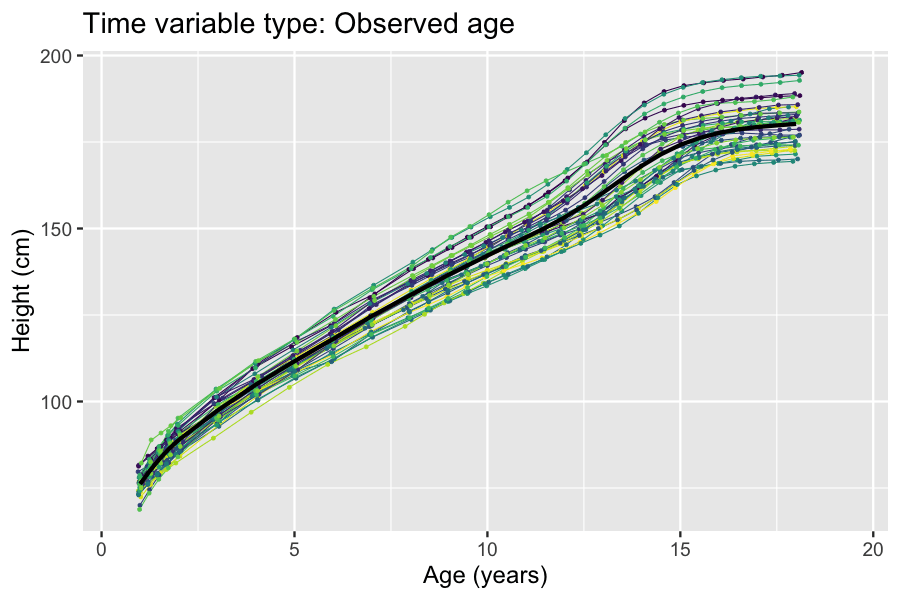
The partial least squares path modeling or partial least squares structural equation modeling (PLS-PM, PLS-SEM) is a method for structural equation modeling that allows estimation of complex cause-effect relationships in path models with latent variables. Overview PLS-PM is a component-based estimation approach that differs from the covariance-based structural equation modeling. Unlike covariance-based approaches to structural equation modeling, PLS-PM does not fit a common factor model to the data, it rather fits a composite model. In doing so, it maximizes the amount of variance explained (though what this means from a statistical point of view is unclear and PLS-PM users do not agree on how this goal might be achieved). In addition, by an adjustment PLS-PM is capable of consistently estimating certain parameters of common factor models as well, through an approach called consistent PLS-PM (PLSc-PM). A further related development is factor-based PLS-PM (PLSF), a variation of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Structural Equation Modeling
Structural equation modeling (SEM) is a label for a diverse set of methods used by scientists in both experimental and observational research across the sciences, business, and other fields. It is used most in the social and behavioral sciences. A definition of SEM is difficult without reference to highly technical language, but a good starting place is the name itself. SEM involves the construction of a '' model'', to represent how various aspects of an observable or theoretical phenomenon are thought to be causally structurally related to one another. The ''structural'' aspect of the model implies theoretical associations between variables that represent the phenomenon under investigation. The postulated causal structuring is often depicted with arrows representing causal connections between variables (as in Figures 1 and 2) but these causal connections can be equivalently represented as equations. The causal structures imply that specific patterns of connections should app ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Latent Variables
In statistics, latent variables (from Latin: present participle of ''lateo'', “lie hidden”) are variables that can only be inferred indirectly through a mathematical model from other observable variables that can be directly observed or measured. Such '' latent variable models'' are used in many disciplines, including political science, demography, engineering, medicine, ecology, physics, machine learning/artificial intelligence, bioinformatics, chemometrics, natural language processing, management and the social sciences. Latent variables may correspond to aspects of physical reality. These could in principle be measured, but may not be for practical reasons. In this situation, the term ''hidden variables'' is commonly used (reflecting the fact that the variables are meaningful, but not observable). Other latent variables correspond to abstract concepts, like categories, behavioral or mental states, or data structures. The terms ''hypothetical variables'' or ''hypothetical ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Regression
In statistics, linear regression is a linear approach for modelling the relationship between a scalar response and one or more explanatory variables (also known as dependent and independent variables). The case of one explanatory variable is called '' simple linear regression''; for more than one, the process is called multiple linear regression. This term is distinct from multivariate linear regression, where multiple correlated dependent variables are predicted, rather than a single scalar variable. In linear regression, the relationships are modeled using linear predictor functions whose unknown model parameters are estimated from the data. Such models are called linear models. Most commonly, the conditional mean of the response given the values of the explanatory variables (or predictors) is assumed to be an affine function of those values; less commonly, the conditional median or some other quantile is used. Like all forms of regression analysis, linear regressio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Partial Least Squares Regression
Partial least squares regression (PLS regression) is a statistical method that bears some relation to principal components regression; instead of finding hyperplanes of maximum variance between the response and independent variables, it finds a linear regression model by projecting the predicted variables and the observable variables to a new space. Because both the ''X'' and ''Y'' data are projected to new spaces, the PLS family of methods are known as bilinear factor models. Partial least squares discriminant analysis (PLS-DA) is a variant used when the Y is categorical. PLS is used to find the fundamental relations between two matrices (''X'' and ''Y''), i.e. a latent variable approach to modeling the covariance structures in these two spaces. A PLS model will try to find the multidimensional direction in the ''X'' space that explains the maximum multidimensional variance direction in the ''Y'' space. PLS regression is particularly suited when the matrix of predictors has more ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Principal Component Analysis
Principal component analysis (PCA) is a popular technique for analyzing large datasets containing a high number of dimensions/features per observation, increasing the interpretability of data while preserving the maximum amount of information, and enabling the visualization of multidimensional data. Formally, PCA is a statistical technique for reducing the dimensionality of a dataset. This is accomplished by linearly transforming the data into a new coordinate system where (most of) the variation in the data can be described with fewer dimensions than the initial data. Many studies use the first two principal components in order to plot the data in two dimensions and to visually identify clusters of closely related data points. Principal component analysis has applications in many fields such as population genetics, microbiome studies, and atmospheric science. The principal components of a collection of points in a real coordinate space are a sequence of p unit vectors, where the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Structural Equation Modeling
Structural equation modeling (SEM) is a label for a diverse set of methods used by scientists in both experimental and observational research across the sciences, business, and other fields. It is used most in the social and behavioral sciences. A definition of SEM is difficult without reference to highly technical language, but a good starting place is the name itself. SEM involves the construction of a '' model'', to represent how various aspects of an observable or theoretical phenomenon are thought to be causally structurally related to one another. The ''structural'' aspect of the model implies theoretical associations between variables that represent the phenomenon under investigation. The postulated causal structuring is often depicted with arrows representing causal connections between variables (as in Figures 1 and 2) but these causal connections can be equivalently represented as equations. The causal structures imply that specific patterns of connections should app ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Least Squares
The method of least squares is a standard approach in regression analysis to approximate the solution of overdetermined systems (sets of equations in which there are more equations than unknowns) by minimizing the sum of the squares of the residuals (a residual being the difference between an observed value and the fitted value provided by a model) made in the results of each individual equation. The most important application is in data fitting. When the problem has substantial uncertainties in the independent variable (the ''x'' variable), then simple regression and least-squares methods have problems; in such cases, the methodology required for fitting errors-in-variables models may be considered instead of that for least squares. Least squares problems fall into two categories: linear or ordinary least squares and nonlinear least squares, depending on whether or not the residuals are linear in all unknowns. The linear least-squares problem occurs in statistical regr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Graphical Models
''Graphical Models'' is an academic journal in computer graphics and geometry processing publisher by Elsevier. , its editor-in-chief is Jorg Peters of the University of Florida. History This journal has gone through multiple names. Founded in 1972 as ''Computer Graphics and Image Processing'' by Azriel Rosenfeld, it became the first journal to focus on computer image analysis. Its first change of name came in 1983, when it became ''Computer Vision, Graphics, and Image Processing''. In 1991 it split into two journals, ''CVGIP: Graphical Models and Image Processing'', and ''CVGIP: Image Understanding'', which later became ''Computer Vision and Image Understanding''. Meanwhile, in 1995, the journal ''Graphical Models and Image Processing'' removed the "CVGIP" prefix from its former name, and finally took its current title, ''Graphical Models'', in 2002. Ranking Although initially ranked by SCImago Journal Rank The SCImago Journal Rank (SJR) indicator is a measure of the presti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |