|
Oversampling
In signal processing, oversampling is the process of sampling a signal at a sampling frequency significantly higher than the Nyquist rate. Theoretically, a bandwidth-limited signal can be perfectly reconstructed if sampled at the Nyquist rate or above it. The Nyquist rate is defined as twice the bandwidth of the signal. Oversampling is capable of improving resolution and signal-to-noise ratio, and can be helpful in avoiding aliasing and phase distortion by relaxing anti-aliasing filter performance requirements. A signal is said to be oversampled by a factor of ''N'' if it is sampled at ''N'' times the Nyquist rate. Motivation There are three main reasons for performing oversampling: to improve anti-aliasing performance, to increase resolution and to reduce noise. Anti-aliasing Oversampling can make it easier to realize analog anti-aliasing filters. Without oversampling, it is very difficult to implement filters with the sharp cutoff necessary to maximize use of the availab ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Resolution (audio)
In digital audio using pulse-code modulation (PCM), bit depth is the number of bits of information in each sample, and it directly corresponds to the resolution of each sample. Examples of bit depth include Compact Disc Digital Audio, which uses 16 bits per sample, and DVD-Audio and Blu-ray Disc which can support up to 24 bits per sample. In basic implementations, variations in bit depth primarily affect the noise level from quantization error—thus the signal-to-noise ratio (SNR) and dynamic range. However, techniques such as dithering, noise shaping, and oversampling can mitigate these effects without changing the bit depth. Bit depth also affects bit rate and file size. Bit depth is only meaningful in reference to a PCM digital signal. Non-PCM formats, such as lossy compression formats, do not have associated bit depths. Binary representation A PCM signal is a sequence of digital audio samples containing the data providing the necessary information to reconstruc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
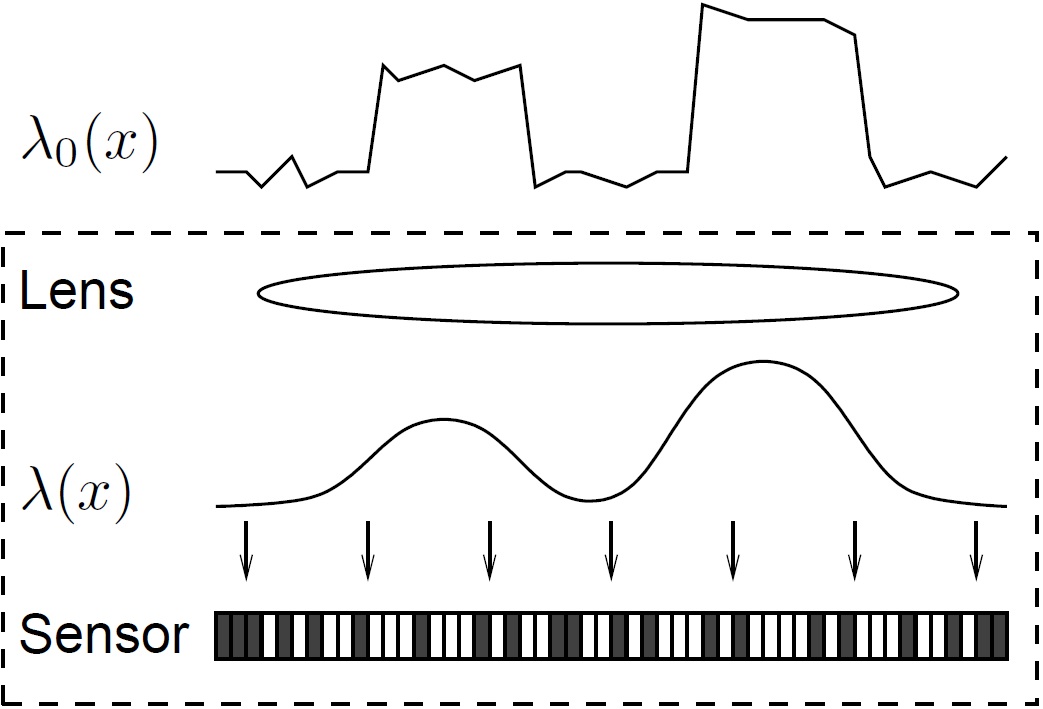
Oversampled Binary Image Sensor
An oversampled binary image sensor is an image sensor with non-linear response capabilities reminiscent of traditional photographic film. Each pixel in the sensor has a binary response, giving only a one-bit quantized measurement of the local light intensity. The response function of the image sensor is non-linear and similar to a logarithmic function, which makes the sensor suitable for high dynamic range imaging. Working principle Before the advent of digital image sensors, photography, for the most part of its history, used film to record light information. At the heart of every photographic film are a large number of light-sensitive grains of silver-halide crystals.T. H. James, The Theory of The Photographic Process, 4th ed., New York: Macmillan Publishing Co., Inc., 1977. During exposure, each micron-sized grain has a binary fate: Either it is struck by some incident photons and becomes "exposed", or it is missed by the photon bombardment and remains "unexposed". In the subseq ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Delta-sigma Modulation
Delta-sigma (ΔΣ; or sigma-delta, ΣΔ) modulation is a method for encoding analog signals into digital signals as found in an analog-to-digital converter (ADC). It is also used to convert high bit-count, low-frequency digital signals into lower bit-count, higher-frequency digital signals as part of the process to convert digital signals into analog as part of a digital-to-analog converter (DAC). In a conventional ADC, an analog signal is sampled with a sampling frequency and subsequently quantized in a multi-level quantizer into a digital signal. This process introduces quantization error noise. The first step in a delta-sigma modulation is delta modulation. In delta modulation the change in the signal (its delta) is encoded, rather than the absolute value. The result is a stream of pulses, as opposed to a stream of numbers as is the case with pulse-code modulation (PCM). In delta-sigma modulation, accuracy of the modulation is improved by passing the digital output thro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sampling (signal Processing)
In signal processing, sampling is the reduction of a continuous-time signal to a discrete-time signal. A common example is the conversion of a sound wave to a sequence of "samples". A sample is a value of the signal at a point in time and/or space; this definition differs from the usage in statistics, which refers to a set of such values. A sampler is a subsystem or operation that extracts samples from a continuous signal. A theoretical ideal sampler produces samples equivalent to the instantaneous value of the continuous signal at the desired points. The original signal can be reconstructed from a sequence of samples, up to the Nyquist limit, by passing the sequence of samples through a type of low-pass filter called a reconstruction filter. Theory Functions of space, time, or any other dimension can be sampled, and similarly in two or more dimensions. For functions that vary with time, let ''S''(''t'') be a continuous function (or "signal") to be sampled, and let s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Analog-to-digital Converter
In electronics, an analog-to-digital converter (ADC, A/D, or A-to-D) is a system that converts an analog signal, such as a sound picked up by a microphone or light entering a digital camera, into a digital signal. An ADC may also provide an isolated measurement such as an electronic device that converts an analog input voltage or current to a digital number representing the magnitude of the voltage or current. Typically the digital output is a two's complement binary number that is proportional to the input, but there are other possibilities. There are several ADC architectures. Due to the complexity and the need for precisely matched components, all but the most specialized ADCs are implemented as integrated circuits (ICs). These typically take the form of metal–oxide–semiconductor (MOS) mixed-signal integrated circuit chips that integrate both analog and digital circuits. A digital-to-analog converter (DAC) performs the reverse function; it converts a digita ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
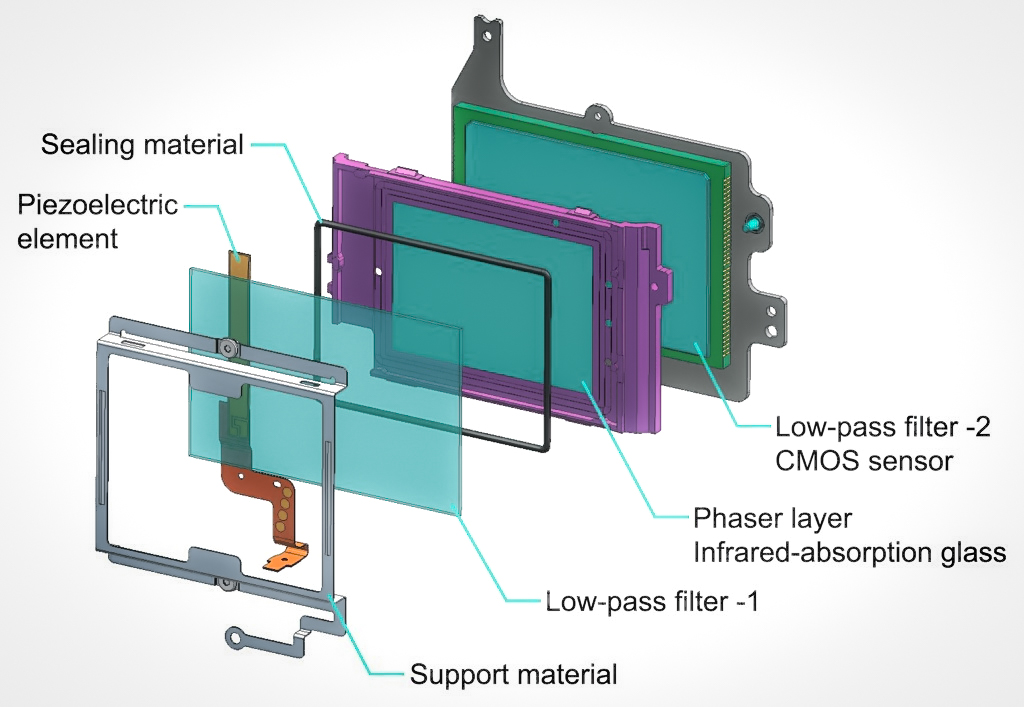
Anti-aliasing Filter
An anti-aliasing filter (AAF) is a filter used before a signal sampler to restrict the bandwidth of a signal to satisfy the Nyquist–Shannon sampling theorem over the band of interest. Since the theorem states that unambiguous reconstruction of the signal from its samples is possible when the power of frequencies above the Nyquist frequency is zero, a brick wall filter is an idealized but impractical AAF. A practical AAF makes a trade off between reduced bandwidth and increased aliasing. A practical anti-aliasing filter will typically permit some aliasing to occur or attenuate or otherwise distort some in-band frequencies close to the Nyquist limit. For this reason, many practical systems sample higher than would be theoretically required by a perfect AAF in order to ensure that all frequencies of interest can be reconstructed, a practice called oversampling. Optical applications The Pentax K-3 from Ricoh introduced a unique sensor-based anti-aliasing filter. Th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nyquist–Shannon Sampling Theorem
The Nyquist–Shannon sampling theorem is a theorem in the field of signal processing which serves as a fundamental bridge between continuous-time signals and discrete-time signals. It establishes a sufficient condition for a sample rate that permits a discrete sequence of ''samples'' to capture all the information from a continuous-time signal of finite bandwidth. Strictly speaking, the theorem only applies to a class of mathematical functions having a Fourier transform that is zero outside of a finite region of frequencies. Intuitively we expect that when one reduces a continuous function to a discrete sequence and interpolates back to a continuous function, the fidelity of the result depends on the density (or sample rate) of the original samples. The sampling theorem introduces the concept of a sample rate that is sufficient for perfect fidelity for the class of functions that are band-limited to a given bandwidth, such that no actual information is lost in the sampling proc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reconstruction Filter
In a mixed-signal system (analog and digital), a reconstruction filter, sometimes called an anti-imaging filter, is used to construct a smooth analog signal from a digital input, as in the case of a digital to analog converter ( DAC) or other sampled data output device. Sampled data reconstruction filters The sampling theorem describes why the input of an ADC requires a low-pass analog electronic filter, called the anti-aliasing filter: the sampled ''input'' signal must be bandlimited to prevent aliasing (here meaning waves of higher frequency being ''recorded'' as a lower frequency). For the same reason, the output of a DAC requires a low-pass analog filter, called a reconstruction filter - because the ''output'' signal must be bandlimited, to prevent imaging (meaning Fourier coefficients being reconstructed as spurious high-frequency 'mirrors'). This is an implementation of the Whittaker–Shannon interpolation formula. Ideally, both filters should be brickwall filters, constan ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Digital-to-analog Converter
In electronics, a digital-to-analog converter (DAC, D/A, D2A, or D-to-A) is a system that converts a digital signal into an analog signal. An analog-to-digital converter (ADC) performs the reverse function. There are several DAC architectures; the suitability of a DAC for a particular application is determined by figures of merit including: resolution, maximum sampling frequency and others. Digital-to-analog conversion can degrade a signal, so a DAC should be specified that has insignificant errors in terms of the application. DACs are commonly used in music players to convert digital data streams into analog audio signals. They are also used in televisions and mobile phones to convert digital video data into analog video signals. These two applications use DACs at opposite ends of the frequency/resolution trade-off. The audio DAC is a low-frequency, high-resolution type while the video DAC is a high-frequency low- to medium-resolution type. Due to the comple ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nyquist Limit
In signal processing, the Nyquist frequency (or folding frequency), named after Harry Nyquist, is a characteristic of a sampler, which converts a continuous function or signal into a discrete sequence. In units of cycles per second ( Hz), its value is one-half of the sampling rate (samples per second). When the highest frequency ( bandwidth) of a signal is less than the Nyquist frequency of the sampler, the resulting discrete-time sequence is said to be free of the distortion known as aliasing, and the corresponding sample rate is said to be above the Nyquist rate for that particular signal. In a typical application of sampling, one first chooses the highest frequency to be preserved and recreated, based on the expected content (voice, music, etc.) and desired fidelity. Then one inserts an anti-aliasing filter ahead of the sampler. Its job is to attenuate the frequencies above that limit. Finally, based on the characteristics of the filter, one chooses a sample rate (and c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Noise Power
In telecommunication, the term noise power has the following meanings: # The measured total noise in a given bandwidth at the input or output of a device when the signal is not present; the integral of noise spectral density over the bandwidth # The power generated by a random electromagnetic process. # Interfering and unwanted power in an electrical device or system. # In the acceptance testing of radio transmitters, the mean power supplied to the antenna transmission line by a radio transmitter when loaded with noise having a Gaussian amplitude-vs.-frequency Frequency is the number of occurrences of a repeating event per unit of time. It is also occasionally referred to as ''temporal frequency'' for clarity, and is distinct from '' angular frequency''. Frequency is measured in hertz (Hz) which is ... distribution. References Telecommunication theory Noise (electronics) {{telecomm-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nyquist Rate
In signal processing, the Nyquist rate, named after Harry Nyquist, is a value (in units of samples per second or hertz, Hz) equal to twice the highest frequency ( bandwidth) of a given function or signal. When the function is digitized at a higher sample rate (see ), the resulting discrete-time sequence is said to be free of the distortion known as aliasing. Conversely, for a given sample-rate the corresponding Nyquist frequency in Hz is one-half the sample-rate. Note that the ''Nyquist rate'' is a property of a continuous-time signal, whereas ''Nyquist frequency'' is a property of a discrete-time system. The term ''Nyquist rate'' is also used in a different context with units of symbols per second, which is actually the field in which Harry Nyquist was working. In that context it is an upper bound for the symbol rate across a bandwidth-limited baseband channel such as a telegraph line or passband channel such as a limited radio frequency band or a frequency division m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |