|
Optimal Substructure
In computer science, a problem is said to have optimal substructure if an optimal solution can be constructed from optimal solutions of its subproblems. This property is used to determine the usefulness of greedy algorithms for a problem.{{cite book, title=Introduction to Algorithms , edition=3rd, last1=Cormen, first1=Thomas H. , last2=Leiserson , first2=Charles E. , last3=Rivest, first3=Ronald L. , last4= Stein , first4=Clifford, date=2009 , isbn=978-0-262-03384-8, publisher=MIT Press, authorlink1=Thomas H. Cormen , authorlink2=Charles E. Leiserson, authorlink3=Ron Rivest , authorlink4=Clifford Stein Typically, a greedy algorithm is used to solve a problem with optimal substructure if it can be proven by induction that this is optimal at each step. Otherwise, provided the problem exhibits overlapping subproblems as well, divide-and-conquer methods or dynamic programming may be used. If there are no appropriate greedy algorithms and the problem fails to exhibit overlapping sub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Partition Of A Set
In mathematics, a partition of a set is a grouping of its elements into Empty set, non-empty subsets, in such a way that every element is included in exactly one subset. Every equivalence relation on a Set (mathematics), set defines a partition of this set, and every partition defines an equivalence relation. A set equipped with an equivalence relation or a partition is sometimes called a setoid, typically in type theory and proof theory. Definition and notation A partition of a set ''X'' is a set of non-empty subsets of ''X'' such that every element ''x'' in ''X'' is in exactly one of these subsets (i.e., the subsets are nonempty mutually disjoint sets). Equivalently, a family of sets ''P'' is a partition of ''X'' if and only if all of the following conditions hold: *The family ''P'' does not contain the empty set (that is \emptyset \notin P). *The union (set theory), union of the sets in ''P'' is equal to ''X'' (that is \textstyle\bigcup_ A = X). The sets in ''P'' are said ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Longest Path Problem
In graph theory and theoretical computer science, the longest path problem is the problem of finding a simple path of maximum length in a given graph. A path is called ''simple'' if it does not have any repeated vertices; the length of a path may either be measured by its number of edges, or (in weighted graphs) by the sum of the weights of its edges. In contrast to the shortest path problem, which can be solved in polynomial time in graphs without negative-weight cycles, the longest path problem is NP-hard and the decision version of the problem, which asks whether a path exists of at least some given length, is NP-complete. This means that the decision problem cannot be solved in polynomial time for arbitrary graphs unless P = NP. Stronger hardness results are also known showing that it is difficult to approximate. However, it has a linear time solution for directed acyclic graphs, which has important applications in finding the critical path in scheduling problems. NP-hardnes ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Shortest Path Problem
In graph theory, the shortest path problem is the problem of finding a path between two vertices (or nodes) in a graph such that the sum of the weights of its constituent edges is minimized. The problem of finding the shortest path between two intersections on a road map may be modeled as a special case of the shortest path problem in graphs, where the vertices correspond to intersections and the edges correspond to road segments, each weighted by the length or distance of each segment. Definition The shortest path problem can be defined for graphs whether undirected, directed, or mixed. The definition for undirected graphs states that every edge can be traversed in either direction. Directed graphs require that consecutive vertices be connected by an appropriate directed edge. Two vertices are adjacent when they are both incident to a common edge. A path in an undirected graph is a sequence of vertices P = ( v_1, v_2, \ldots, v_n ) \in V \times V \times \cdots \times V ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Longest Palindromic Substring
In computer science, the longest palindromic substring or longest symmetric factor problem is the problem of finding a maximum-length contiguous substring of a given string that is also a palindrome. For example, the longest palindromic substring of "bananas" is "anana". The longest palindromic substring is not guaranteed to be unique; for example, in the string "abracadabra", there is no palindromic substring with length greater than three, but there are two palindromic substrings with length three, namely, "aca" and "ada". In some applications it may be necessary to return all maximal palindromic substrings (that is, all substrings that are themselves palindromes and cannot be extended to larger palindromic substrings) rather than returning only one substring or returning the maximum length of a palindromic substring. invented an O(n)-time algorithm for listing all the palindromes that appear at the start of a given string of length n. However, as observed e.g., by , the same alg ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Longest Increasing Subsequence
In computer science, the longest increasing subsequence problem aims to find a subsequence of a given sequence in which the subsequence's elements are sorted in an ascending order and in which the subsequence is as long as possible. This subsequence is not necessarily contiguous or unique. The longest increasing subsequences are studied in the context of various disciplines related to mathematics, including algorithmics, random matrix theory, representation theory, and physics. The longest increasing subsequence problem is solvable in time O(n \log n), where n denotes the length of the input sequence. Example In the first 16 terms of the binary Van der Corput sequence :0, 8, 4, 12, 2, 10, 6, 14, 1, 9, 5, 13, 3, 11, 7, 15 one of the longest increasing subsequences is :0, 2, 6, 9, 11, 15. This subsequence has length six; the input sequence has no seven-member increasing subsequences. The longest increasing subsequence in this example is not the only solution: for instance, :0, 4, 6, 9 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Longest Common Subsequence Problem
A longest common subsequence (LCS) is the longest subsequence common to all sequences in a set of sequences (often just two sequences). It differs from the longest common substring: unlike substrings, subsequences are not required to occupy consecutive positions within the original sequences. The problem of computing longest common subsequences is a classic computer science problem, the basis of data comparison programs such as the diff utility, and has applications in computational linguistics and bioinformatics. It is also widely used by revision control systems such as Git for reconciling multiple changes made to a revision-controlled collection of files. For example, consider the sequences (ABCD) and (ACBAD). They have five length-2 common subsequences: (AB), (AC), (AD), (BD), and (CD); two length-3 common subsequences: (ABD) and (ACD); and no longer common subsequences. So (ABD) and (ACD) are their longest common subsequences. Complexity For the general case of an ar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Shortest Path Problem
In graph theory, the shortest path problem is the problem of finding a path between two vertices (or nodes) in a graph such that the sum of the weights of its constituent edges is minimized. The problem of finding the shortest path between two intersections on a road map may be modeled as a special case of the shortest path problem in graphs, where the vertices correspond to intersections and the edges correspond to road segments, each weighted by the length or distance of each segment. Definition The shortest path problem can be defined for graphs whether undirected, directed, or mixed. The definition for undirected graphs states that every edge can be traversed in either direction. Directed graphs require that consecutive vertices be connected by an appropriate directed edge. Two vertices are adjacent when they are both incident to a common edge. A path in an undirected graph is a sequence of vertices P = ( v_1, v_2, \ldots, v_n ) \in V \times V \times \cdots \times V ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Computer Science
Computer science is the study of computation, information, and automation. Computer science spans Theoretical computer science, theoretical disciplines (such as algorithms, theory of computation, and information theory) to Applied science, applied disciplines (including the design and implementation of Computer architecture, hardware and Software engineering, software). Algorithms and data structures are central to computer science. The theory of computation concerns abstract models of computation and general classes of computational problem, problems that can be solved using them. The fields of cryptography and computer security involve studying the means for secure communication and preventing security vulnerabilities. Computer graphics (computer science), Computer graphics and computational geometry address the generation of images. Programming language theory considers different ways to describe computational processes, and database theory concerns the management of re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
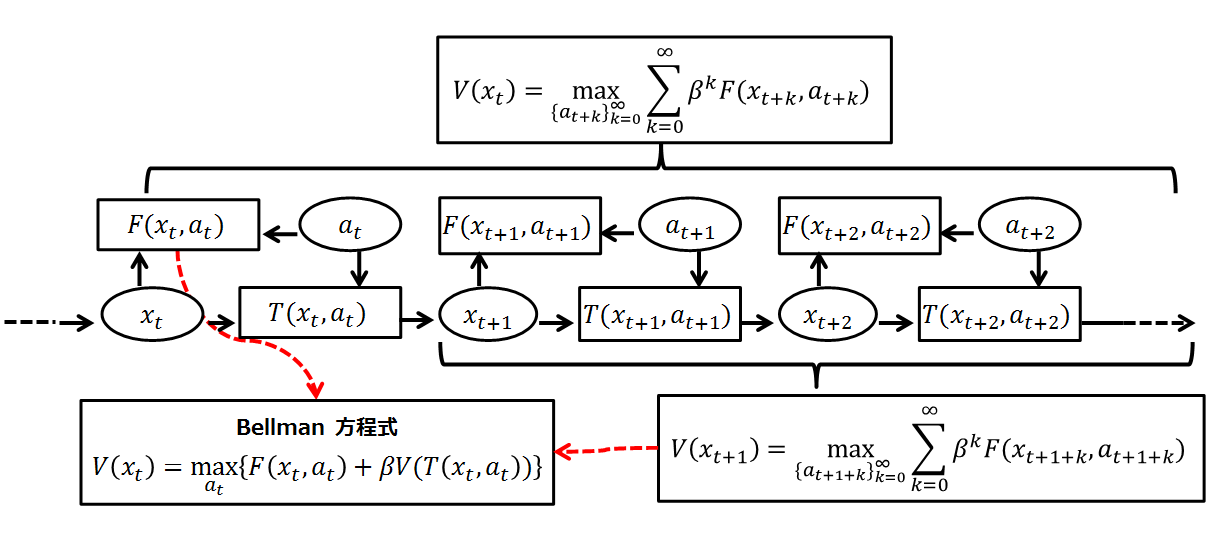
Bellman Equation
A Bellman equation, named after Richard E. Bellman, is a necessary condition for optimality associated with the mathematical Optimization (mathematics), optimization method known as dynamic programming. It writes the "value" of a decision problem at a certain point in time in terms of the payoff from some initial choices and the "value" of the remaining decision problem that results from those initial choices. This breaks a dynamic optimization problem into a sequence of simpler subproblems, as Bellman's “principle of optimality" prescribes. The equation applies to algebraic structures with a total ordering; for algebraic structures with a partial ordering, the generic Bellman's equation can be used. The Bellman equation was first applied to engineering control theory and to other topics in applied mathematics, and subsequently became an important tool in economic theory; though the basic concepts of dynamic programming are prefigured in John von Neumann and Oskar Morgenstern's ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |