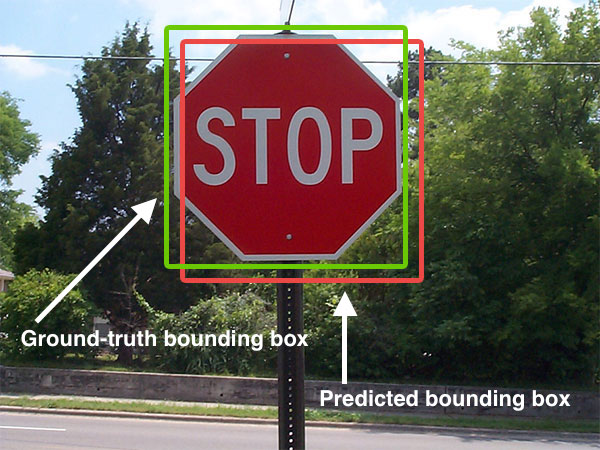
|
Opening (morphology)
In mathematical morphology, opening is the dilation of the erosion of a set A by a structuring element B: :A\circ B = (A\ominus B)\oplus B, \, where \ominus and \oplus denote erosion and dilation, respectively. Together with closing, the opening serves in computer vision and image processing as a basic workhorse of morphological noise removal. Opening removes small objects from the foreground (usually taken as the bright pixels) of an image, placing them in the background, while closing removes small holes in the foreground, changing small islands of background into foreground. These techniques can also be used to find specific shapes in an image. Opening can be used to find things into which a specific structuring element can fit (edges, corners, ...). One can think of ''B'' sweeping around the inside of the boundary of ''A'', so that it does not extend beyond the boundary, and shaping the ''A'' boundary around the boundary of the element. Properties * Opening is idempote ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Opening
Opening may refer to: Types of openings * Hole * A title sequence or opening credits * Grand opening of a business or other institution * Inauguration * Keynote * Opening sentence * Opening sequence * Opening statement, a beginning statement in a court case * Opening (morphology), a morphological filtering operation used in image processing * Overture * Salutation (greeting) * Vernissage Games * Backgammon opening * Chess opening * Go opening * Shogi opening * , a term from contract bridge * , a term from contract bridge Media * Al-Fatiha, "The Opening", the first chapter of the Qur'an * ''The Opening'' (album), live album by Mal Waldron * "Opening", a song by Hikaru Utada from the 2004 album '' Exodus'' * "Opening", a song by Jay Chou from the 2007 album ''Secret Secrecy is the practice of hiding information from certain individuals or groups who do not have the "need to know", perhaps while sharing it with other individuals. That which is kept hidden is known ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Mathematical Morphology
Mathematical morphology (MM) is a theory and technique for the analysis and processing of Geometry, geometrical structures, based on set theory, lattice theory, topology, and random functions. MM is most commonly applied to digital images, but it can be employed as well on Graph (discrete mathematics), graphs, polygon mesh, surface meshes, Solid geometry, solids, and many other spatial structures. Topology, Topological and Geometry, geometrical continuum (theory), continuous-space concepts such as size, shape, convex set, convexity, Connectedness, connectivity, and geodesic distance, were introduced by MM on both continuous and discrete spaces. MM is also the foundation of morphological image processing, which consists of a set of operators that transform images according to the above characterizations. The basic morphological operators are Erosion (morphology), erosion, Dilation (morphology), dilation, Opening (morphology), opening and Closing (morphology), closing. MM was orig ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Dilation (morphology)
Dilation (usually represented by ⊕) is one of the basic operations in mathematical morphology. Originally developed for binary images, it has been expanded first to grayscale images, and then to complete lattices. The dilation operation usually uses a structuring element for probing and expanding the shapes contained in the input image. Binary dilation In binary morphology, dilation is a shift-invariant (Translational invariance, translation invariant) operator, equivalent to Minkowski addition. A binary image is viewed in mathematical morphology as a subset of a Euclidean space R''d'' or the integer grid Z''d'', for some dimension ''d''. Let ''E'' be a Euclidean space or an integer grid, ''A'' a binary image in ''E'', and ''B'' a structuring element regarded as a subset of R''d''. The dilation of ''A'' by ''B'' is defined by ::A \oplus B = \bigcup_ A_b, where ''A''''b'' is the translation of ''A'' by ''b''. Dilation is commutative, also given by A \oplus B = B\oplus A = ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Erosion (morphology)
Erosion (usually represented by ⊖) is one of two fundamental operations (the other being dilation) in morphological image processing from which all other morphological operations are based. It was originally defined for binary images, later being extended to grayscale images, and subsequently to complete lattices. The erosion operation usually uses a structuring element for probing and reducing the shapes contained in the input image. Binary erosion In binary morphology, an image is viewed as a subset of a Euclidean space \mathbb^d or the integer grid \mathbb^d, for some dimension ''d''. The basic idea in binary morphology is to probe an image with a simple, pre-defined shape, drawing conclusions on how this shape fits or misses the shapes in the image. This simple "probe" is called structuring element, and is itself a binary image (i.e., a subset of the space or grid). Let ''E'' be a Euclidean space or an integer grid, and ''A'' a binary image in ''E''. The erosion of th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Set (mathematics)
In mathematics, a set is a collection of different things; the things are '' elements'' or ''members'' of the set and are typically mathematical objects: numbers, symbols, points in space, lines, other geometric shapes, variables, or other sets. A set may be finite or infinite. There is a unique set with no elements, called the empty set; a set with a single element is a singleton. Sets are ubiquitous in modern mathematics. Indeed, set theory, more specifically Zermelo–Fraenkel set theory, has been the standard way to provide rigorous foundations for all branches of mathematics since the first half of the 20th century. Context Before the end of the 19th century, sets were not studied specifically, and were not clearly distinguished from sequences. Most mathematicians considered infinity as potentialmeaning that it is the result of an endless processand were reluctant to consider infinite sets, that is sets whose number of members is not a natural number. Specific ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Structuring Element
In mathematical morphology, a structuring element is a shape, used to probe or interact with a given image, with the purpose of drawing conclusions on how this shape fits or misses the shapes in the image. It is typically used in morphological operations, such as dilation, erosion, opening, and closing, as well as the hit-or-miss transform. According to Georges Matheron, knowledge about an object (e.g., an image) depends on the manner in which we probe (observe) it.See ( Dougherty 1992), chapter 1, page 1. In particular, the choice of a certain structuring element for a particular morphological operation influences the information one can obtain. There are two main characteristics that are directly related to structuring elements: * Shape. For example, the structuring element can be a "ball" or a line; convex or a ring, etc. By choosing a particular structuring element, one sets a way of differentiating some objects (or parts of objects) from others, according to their shape or ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Closing (morphology)
In mathematical morphology, the closing of a set (binary image) ''A'' by a structuring element ''B'' is the erosion of the dilation of that set, :A\bullet B = (A\oplus B)\ominus B, \, where \oplus and \ominus denote the dilation and erosion, respectively. In image processing, closing is, together with opening, the basic workhorse of morphological noise removal. Opening removes small objects, while closing removes small holes. Example Perform Dilation ( A\oplus B ): Suppose A is the following 11 x 11 matrix and B is the following 3 x 3 matrix: 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 0 0 1 1 1 0 0 1 1 1 1 0 0 1 1 1 0 0 1 1 1 1 1 1 1 1 1 0 0 1 1 1 1 0 0 0 1 1 0 1 1 1 0 1 1 1 1 0 0 0 1 1 0 1 1 1 0 1 0 0 1 0 0 0 1 1 0 1 1 1 0 1 0 0 1 1 1 1 1 1 0 0 1 1 1 1 1 1 1 0 0 0 0 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 For each pixel in A that has a value of 1, superimpose B, with t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Computer Vision
Computer vision tasks include methods for image sensor, acquiring, Image processing, processing, Image analysis, analyzing, and understanding digital images, and extraction of high-dimensional data from the real world in order to produce numerical or symbolic information, e.g. in the form of decisions. "Understanding" in this context signifies the transformation of visual images (the input to the retina) into descriptions of the world that make sense to thought processes and can elicit appropriate action. This image understanding can be seen as the disentangling of symbolic information from image data using models constructed with the aid of geometry, physics, statistics, and learning theory. The scientific discipline of computer vision is concerned with the theory behind artificial systems that extract information from images. Image data can take many forms, such as video sequences, views from multiple cameras, multi-dimensional data from a 3D scanning, 3D scanner, 3D point clouds ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Image Processing
An image or picture is a visual representation. An image can be two-dimensional, such as a drawing, painting, or photograph, or three-dimensional, such as a carving or sculpture. Images may be displayed through other media, including a projection on a surface, activation of electronic signals, or digital displays; they can also be reproduced through mechanical means, such as photography, printmaking, or photocopying. Images can also be animated through digital or physical processes. In the context of signal processing, an image is a distributed amplitude of color(s). In optics, the term ''image'' (or ''optical image'') refers specifically to the reproduction of an object formed by light waves coming from the object. A ''volatile image'' exists or is perceived only for a short period. This may be a reflection of an object by a mirror, a projection of a camera obscura, or a scene displayed on a cathode-ray tube. A ''fixed image'', also called a hard copy, is one that ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Idempotent
Idempotence (, ) is the property of certain operations in mathematics and computer science whereby they can be applied multiple times without changing the result beyond the initial application. The concept of idempotence arises in a number of places in abstract algebra (in particular, in the theory of projectors and closure operators) and functional programming (in which it is connected to the property of referential transparency). The term was introduced by American mathematician Benjamin Peirce in 1870 in the context of elements of algebras that remain invariant when raised to a positive integer power, and literally means "(the quality of having) the same power", from + '' potence'' (same + power). Definition An element x of a set S equipped with a binary operator \cdot is said to be ''idempotent'' under \cdot if : . The ''binary operation'' \cdot is said to be ''idempotent'' if : . Examples * In the monoid (\mathbb, \times) of the natural numbers with multiplication, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Increasing
In mathematics, a monotonic function (or monotone function) is a function between ordered sets that preserves or reverses the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order theory. In calculus and analysis In calculus, a function f defined on a subset of the real numbers with real values is called ''monotonic'' if it is either entirely non-decreasing, or entirely non-increasing. That is, as per Fig. 1, a function that increases monotonically does not exclusively have to increase, it simply must not decrease. A function is termed ''monotonically increasing'' (also ''increasing'' or ''non-decreasing'') if for all x and y such that x \leq y one has f\!\left(x\right) \leq f\!\left(y\right), so f preserves the order (see Figure 1). Likewise, a function is called ''monotonically decreasing'' (also ''decreasing'' or ''non-increasing'') if, whenever x \leq y, then f\!\left(x\right) \geq f\!\left(y\right), so i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |