|
Neusis Construction
In geometry, the neusis (; ; plural: ) is a geometric construction method that was used in antiquity by Greek mathematicians. Geometric construction The neusis construction consists of fitting a line element of given length () in between two given lines ( and ), in such a way that the line element, or its extension, passes through a given point . That is, one end of the line element has to lie on , the other end on , while the line element is "inclined" towards . Point is called the pole of the neusis, line the directrix, or guiding line, and line the catch line. Length is called the ''diastema'' (). A neusis construction might be performed by means of a marked ruler that is rotatable around the point (this may be done by putting a pin into the point and then pressing the ruler against the pin). In the figure one end of the ruler is marked with a yellow eye with crosshairs: this is the origin of the scale division on the ruler. A second marking on the ruler (the blue ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Neusis En
In geometry, the neusis (; ; plural: ) is a geometric construction method that was used in antiquity by Greek mathematics, Greek mathematicians. Geometric construction The neusis construction consists of fitting a line element of given length () in between two given lines ( and ), in such a way that the line element, or its extension, passes through a given point . That is, one end of the line element has to lie on , the other end on , while the line element is "inclined" towards . Point is called the pole of the neusis, line the directrix, or guiding line, and line the catch line. Length is called the ''diastema'' (). A neusis construction might be performed by means of a marked ruler that is rotatable around the point (this may be done by putting a pin into the point and then pressing the ruler against the pin). In the figure one end of the ruler is marked with a yellow eye with crosshairs: this is the origin of the scale division on the ruler. A second marking on the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pentagon
In geometry, a pentagon () is any five-sided polygon or 5-gon. The sum of the internal angles in a simple polygon, simple pentagon is 540°. A pentagon may be simple or list of self-intersecting polygons, self-intersecting. A self-intersecting ''regular pentagon'' (or ''star polygon, star pentagon'') is called a pentagram. Regular pentagons A ''regular polygon, regular pentagon'' has Schläfli symbol and interior angles of 108°. A ''regular polygon, regular pentagon'' has five lines of reflectional symmetry, and rotational symmetry of order 5 (through 72°, 144°, 216° and 288°). The diagonals of a convex polygon, convex regular pentagon are in the golden ratio to its sides. Given its side length t, its height H (distance from one side to the opposite vertex), width W (distance between two farthest separated points, which equals the diagonal length D) and circumradius R are given by: :\begin H &= \frac~t \approx 1.539~t, \\ W= D &= \frac~t\approx 1.618~t, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
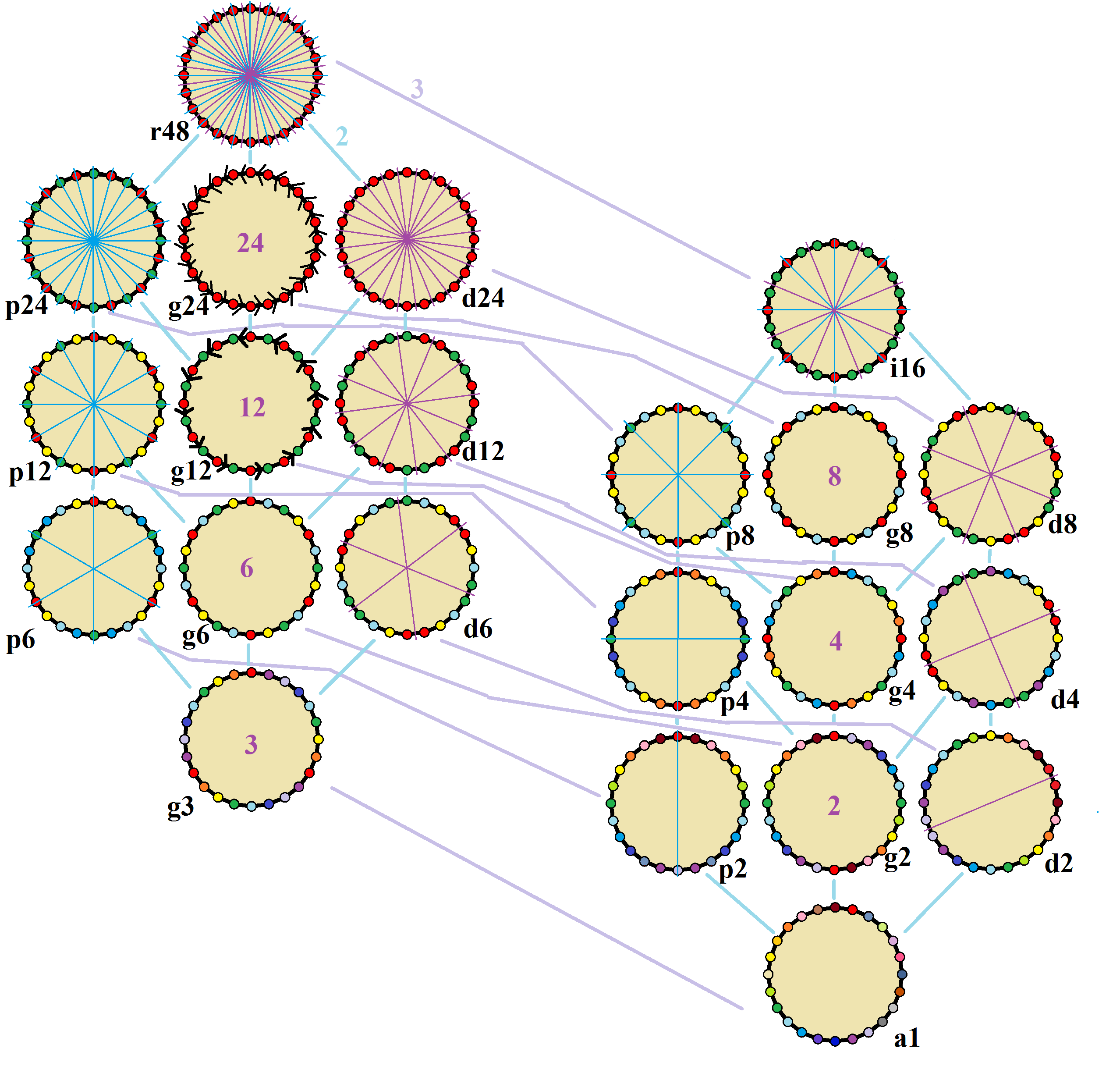
Tridecagon
In geometry, a tridecagon or triskaidecagon or 13-gon is a thirteen-sided polygon. Regular tridecagon A ''regular polygon, regular tridecagon'' is represented by Schläfli symbol . The measure of each internal angle of a Regular polygon, regular tridecagon is approximately 152.308 degree (angle), degrees, and the area with side length ''a'' is given by :A = \fraca^2 \cot \frac \simeq 13.1858\,a^2. Construction As 13 is a Pierpont prime but not a Fermat prime, the regular tridecagon cannot be constructible polygon, constructed using a compass and straightedge. However, it is constructible using neusis construction, neusis, or an angle trisector. The following is an animation from a ''neusis construction'' of a regular tridecagon with radius of circumcircle \overline = 12, according to Andrew M. Gleason, based on the angle trisection by means of the Tomahawk (geometry), Tomahawk (light blue). An approximate construction of a regular tridecagon using straightedge and compass (d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nonagon
In geometry, a nonagon () or enneagon () is a nine-sided polygon or 9-gon. The name ''nonagon'' is a prefix Hybrid word, hybrid formation, from Latin (''nonus'', "ninth" + ''gonon''), used equivalently, attested already in the 16th century in French ''nonogone'' and in English from the 17th century. The name ''enneagon'' comes from Greek language, Greek ''enneagonon'' (εννεα, "nine" + γωνον (from γωνία = "corner")), and is arguably more correct, though less common. Regular nonagon A ''regular polygon, regular nonagon'' is represented by Schläfli symbol and has internal angles of 140°. The area of a regular nonagon of side length ''a'' is given by :A = \fraca^2\cot\frac=(9/2)ar = 9r^2\tan(\pi/9) :::= (9/2)R^2\sin(2\pi/9)\simeq6.18182\,a^2, where the radius ''r'' of the inscribed circle of the regular nonagon is :r=(a/2)\cot(\pi/9) and where ''R'' is the radius of its circumscribed circle: :R = \sqrt=r\sec(\pi/9)=(a/2)\csc(\pi/9). Construction Although a re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Heptagon
In geometry, a heptagon or septagon is a seven-sided polygon or 7-gon. The heptagon is sometimes referred to as the septagon, using ''Wikt:septa-, septa-'' (an elision of ''Wikt:septua-, septua-''), a Latin-derived numerical prefix, rather than ''Wikt:hepta-, hepta-'', a Greek language, Greek-derived numerical prefix (both are cognate), together with the suffix ''-gon'' for , meaning angle. Regular heptagon A regular polygon, regular heptagon, in which all sides and all angles are equal, has internal angles of 5π/7 radians (128 degree (angle), degrees). Its Schläfli symbol is . Area The area (''A'') of a regular heptagon of side length ''a'' is given by: :A = \fraca^2 \cot \frac \simeq 3.634 a^2. This can be seen by subdividing the unit-sided heptagon into seven triangular "pie slices" with Vertex (geometry), vertices at the center and at the heptagon's vertices, and then halving each triangle using the apothem as the common side. The apothem is half the cotangent of \pi/7 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triacontagon
In geometry, a triacontagon or 30-gon is a thirty-sided polygon. The sum of any triacontagon's interior angles is 5040 (number), 5040 degrees. Regular triacontagon The ''regular polygon, regular triacontagon'' is a constructible polygon, by an edge-bisection of a regular pentadecagon, and can also be constructed as a Truncation (geometry), truncated pentadecagon, t. A Truncation (geometry), truncated triacontagon, t, is a hexacontagon, . One interior angle in a regular polygon, regular triacontagon is 168 degrees, meaning that one exterior angle would be 12°. The triacontagon is the largest regular polygon whose interior angle is the sum of the interior angles of smaller polygons: 168° is the sum of the interior angles of the equilateral triangle (60°) and the regular pentagon (108°). The area of a regular triacontagon is (with ) :A = \frac t^2 \cot \frac = \frac t^2 \left(\sqrt + 3\sqrt + \sqrt\sqrt\right) The inradius of a regular triacontagon is :r = \frac t \cot \frac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Icositetragon
In geometry, an icositetragon (or icosikaitetragon) or 24-gon is a twenty-four-sided polygon. The sum of any icositetragon's interior angles is 3960 degrees. Regular icositetragon The ''regular polygon, regular icositetragon'' is represented by Schläfli symbol and can also be constructed as a Truncation (geometry), truncated dodecagon, t, or a twice-truncated hexagon, tt, or thrice-truncated triangle, ttt. One interior angle in a regular polygon, regular icositetragon is 165°, meaning that one exterior angle would be 15°. The area of a regular icositetragon is: (with ''t'' = edge length) : A = 6t^2 \cot \frac = t^2(2+\sqrt+\sqrt+\sqrt). The icositetragon appeared in Archimedes' polygon approximation of pi, along with the hexagon (6-gon), dodecagon (12-gon), tetracontaoctagon (48-gon), and enneacontahexagon (96-gon). Construction As 24 = 23 × 3, a regular icositetragon is constructible polygon, constructible using a compass and straightedge. As a truncated dodecagon, it ca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Icosagon
In geometry, an icosagon or 20-gon is a twenty-sided polygon. The sum of any icosagon's interior angles is 3240 degrees. Regular icosagon The Regular polygon, regular icosagon has Schläfli symbol , and can also be constructed as a Truncation (geometry), truncated decagon, , or a twice-truncated pentagon, . One interior angle in a regular polygon, regular icosagon is 162°, meaning that one exterior angle would be 18°. The area of a regular icosagon with edge length is :A=t^2(1+\sqrt+\sqrt) \simeq 31.5687 t^2. In terms of the radius of its circumcircle, the area is :A=\frac(\sqrt-1); since the area of the circle is \pi R^2, the regular icosagon fills approximately 98.36% of its circumcircle. Uses The Big Wheel on the popular US game show ''The Price Is Right (U.S. game show), The Price Is Right'' has an icosagonal cross-section. The Globe, the outdoor theater used by William Shakespeare's acting company, was discovered to have been built on an icosagonal foundation when ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Heptadecagon
In geometry, a heptadecagon, septadecagon or 17-gon is a seventeen-sided polygon. Regular heptadecagon A ''regular polygon, regular heptadecagon'' is represented by the Schläfli symbol . Construction As 17 is a Fermat prime, the regular heptadecagon is a constructible polygon (that is, one that can be constructed using a straightedge and compass, compass and unmarked straightedge): this was shown by Carl Friedrich Gauss in 1796.Arthur Jones, Sidney A. Morris, Kenneth R. Pearson, ''Abstract Algebra and Famous Impossibilities'', Springer, 1991, p. 178./ref> This proof represented the first progress in regular polygon construction in over 2000 years. Gauss's proof relies firstly on the fact that constructibility is equivalent to expressibility of the trigonometric functions of the common angle in terms of arithmetic operations and square root extractions, and secondly on his proof that this can be done if the odd prime factors of N, the number of sides of the regular polygon, a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hexadecagon
In mathematics, a hexadecagon (sometimes called a hexakaidecagon or 16-gon) is a sixteen-sided polygon. Regular hexadecagon A ''regular polygon, regular hexadecagon'' is a hexadecagon in which all angles are equal and all sides are congruent. Its Schläfli symbol is and can be constructed as a Truncation (geometry), truncated octagon, t, and a twice-truncated square tt. A truncated hexadecagon, t, is a triacontadigon, . Construction As 16 = 24 (a power of two), a regular hexadecagon is constructible polygon, constructible using compass and straightedge: this was already known to ancient Greek mathematicians. Measurements Each angle of a regular hexadecagon is 157.5 Degree (angle), degrees, and the total angle measure of any hexadecagon is 2520 degrees. The area of a regular hexadecagon with edge length ''t'' is :\begin A = 4t^2 \cot \frac =& 4t^2 \left(1+\sqrt+\sqrt\right)\\ =& 4t^2 (\sqrt+1)(\sqrt+1) .\end Because the hexadecagon has a number of sides that is a power of tw ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pentadecagon
In geometry, a pentadecagon or pentakaidecagon or 15-gon is a fifteen-sided polygon. Regular pentadecagon A '' regular pentadecagon'' is represented by Schläfli symbol . A regular pentadecagon has interior angles of 156 °, and with a side length ''a'', has an area given by : \begin A = \fraca^2 \cot \frac & = \frac\sqrta^2 \\ & = \frac \left( \sqrt+\sqrt+ \sqrt\sqrt \right) \\ & \simeq 17.6424\,a^2. \end Construction As 15 = 3 × 5, a product of distinct Fermat primes, a regular pentadecagon is constructible using compass and straightedge: The following constructions of regular pentadecagons with given circumcircle are similar to the illustration of the proposition XVI in Book IV of Euclid's ''Elements''. Compare the construction according to Euclid in this imagePentadecagon In the construction for given circumcircle: \overline = \overline\text \; ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dodecagon
In geometry, a dodecagon, or 12-gon, is any twelve-sided polygon. Regular dodecagon A regular polygon, regular dodecagon is a figure with sides of the same length and internal angles of the same size. It has twelve lines of reflective symmetry and rotational symmetry of order 12. A regular dodecagon is represented by the Schläfli symbol and can be constructed as a Truncation (geometry), truncated hexagon, t, or a twice-truncated triangle, tt. The internal angle at each vertex of a regular dodecagon is 150°. Area The area of a regular dodecagon of side length ''a'' is given by: :\begin A & = 3 \cot\left(\frac \right) a^2 = 3 \left(2+\sqrt \right) a^2 \\ & \simeq 11.19615242\,a^2 \end And in terms of the apothem ''r'' (see also inscribed figure), the area is: :\begin A & = 12 \tan\left(\frac\right) r^2 = 12 \left(2-\sqrt \right) r^2 \\ & \simeq 3.2153903\,r^2 \end In terms of the circumradius '' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |