|
Modal Operator
A modal connective (or modal operator) is a logical connective for modal logic. It is an operator which forms propositions from propositions. In general, a modal operator has the "formal" property of being non- truth-functional in the following sense: The truth-value of composite formulae sometimes depend on factors other than the actual truth-value of their components. In the case of alethic modal logic, a modal operator can be said to be truth-functional in another sense, namely, that of being sensitive only to the distribution of truth-values across possible worlds, actual or not. Finally, a modal operator is "intuitively" characterized by expressing a modal attitude (such as necessity, possibility, belief, or knowledge) about the proposition to which the operator is applied. Syntax for modal operators The syntax rules for modal operators \Box and \Diamond are very similar to those for universal and existential quantifiers; In fact, any formula with modal operators \Box and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Logical Connective
In logic, a logical connective (also called a logical operator, sentential connective, or sentential operator) is a logical constant. Connectives can be used to connect logical formulas. For instance in the syntax of propositional logic, the binary connective \lor can be used to join the two atomic formulas P and Q, rendering the complex formula P \lor Q . Common connectives include negation, disjunction, conjunction, implication, and equivalence. In standard systems of classical logic, these connectives are interpreted as truth functions, though they receive a variety of alternative interpretations in nonclassical logics. Their classical interpretations are similar to the meanings of natural language expressions such as English "not", "or", "and", and "if", but not identical. Discrepancies between natural language connectives and those of classical logic have motivated nonclassical approaches to natural language meaning as well as approaches which pair a classi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
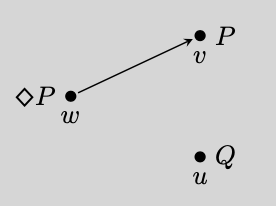 |
Accessibility Relation
An accessibility relation is a relation (math), relation which plays a key role in assigning truth values to sentences in the Kripke semantics, relational semantics for modal logic. In relational semantics, a modal formula's truth value at a ''possible world'' w can depend on what is true at another possible world v, but only if the accessibility relation R relates w to v. For instance, if P holds at some world v such that wRv, the formula \Diamond P will be true at w. The fact wRv is crucial. If R did not relate w to v, then \Diamond P would be false at w unless P also held at some other world u such that wRu. Accessibility relations are motivated conceptually by the fact that natural language linguistic modality, modal statements depend on some, but not all, alternative scenarios. For instance, the sentence "It might be raining" is not generally judged true simply because one can imagine a scenario where it is raining. Rather, its truth depends on whether such a scenario is r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Logical Possibility
Logical possibility refers to a logical proposition that cannot be disproved, using the axioms and rules of a given system of logic. The logical possibility of a proposition will depend upon the system of logic being considered, rather than on the violation of any single rule. Some systems of logic restrict inferences from inconsistent propositions or even allow for true contradictions. Other logical systems have more than two truth-values instead of a binary of such values. Some assume the system in question is classical propositional logic. Similarly, the criterion for logical possibility is often based on whether or not a proposition is contradictory and as such, is often thought of as the broadest type of possibility. In modal logic, a logical proposition is possible if it is true in some possible world. The universe of "possible worlds" depends upon the axioms and rules of the logical system in which one is working, but given some logical system, any logically consist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Causality
Causality is an influence by which one Event (philosophy), event, process, state, or Object (philosophy), object (''a'' ''cause'') contributes to the production of another event, process, state, or object (an ''effect'') where the cause is at least partly responsible for the effect, and the effect is at least partly dependent on the cause. The cause of something may also be described as the reason for the event or process. In general, a process can have multiple causes,Compare: which are also said to be ''causal factors'' for it, and all lie in its past. An effect can in turn be a cause of, or causal factor for, many other effects, which all lie in its future. Some writers have held that causality is metaphysics , metaphysically prior to notions of time and space. Causality is an abstraction that indicates how the world progresses. As such it is a basic concept; it is more apt to be an explanation of other concepts of progression than something to be explained by other more fun ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Possible Worlds
Possible Worlds may refer to: * Possible worlds, concept in philosophy * ''Possible Worlds'' (play), 1990 play by John Mighton ** ''Possible Worlds'' (film), 2000 film by Robert Lepage, based on the play * Possible Worlds (studio) * ''Possible Worlds'', poetry book by Peter Porter * ''Possible Worlds'', book by J. B. S. Haldane * ''Possible Worlds'', 1995 album by Markus Stockhausen See also * * * Possible (other) * World (other) {{dab ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Alethic Modality
Alethic modality (from Greek ἀλήθεια = truth) is a linguistic modality that indicates modalities of truth, in particular the modalities of logical necessity, contingency, possibility and impossibility. Alethic modality is often associated with epistemic modality in research, and it has been questioned whether this modality should be considered distinct from epistemic modality which denotes the speaker's evaluation or judgment of the truth. The criticism states that there is no real difference between "the truth in the world" (alethic) and "the truth in an individual's mind" (epistemic). An investigation has not found a single language in which alethic and epistemic modalities would be formally distinguished, for example by the means of a grammatical mood. In such a language, "A circle can't be square", "can't be" would be expressed by an alethic mood, whereas for "He can't be that wealthy", "can't be" would be expressed by an epistemic mood. As we can see, this is not a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Doxastic Logic
Doxastic logic is a type of logic concerned with reasoning about beliefs. The term ' derives from the Ancient Greek (''doxa'', "opinion, belief"), from which the English term ''doxa'' ("popular opinion or belief") is also borrowed. Typically, a doxastic logic uses the notation \mathcal_c x to mean "reasoner c believes that x is true", and the set \mathbb_c : \left \ denotes the set of beliefs of c. In doxastic logic, belief is treated as a modal operator. There is complete parallelism between a person who believes propositions and a formal system that derives propositions. Using doxastic logic, one can express the epistemic counterpart of Gödel's incompleteness theorem of metalogic, as well as Löb's theorem, and other metalogical results in terms of belief. Smullyan, Raymond M., (1986''Logicians who reason about themselves'' Proceedings of the 1986 conference on Theoretical aspects of reasoning about knowledge, Monterey (CA), Morgan Kaufmann Publishers Inc., San Francis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Epistemic Modal Logic
Epistemic modal logic is a subfield of modal logic that is concerned with reasoning about knowledge. While epistemology has a long philosophical tradition dating back to Ancient Greece, epistemic logic is a much more recent development with applications in many fields, including philosophy, theoretical computer science, artificial intelligence, economics, and linguistics. While philosophers since Aristotle have discussed modal logic, and Medieval philosophers such as Avicenna, Ockham, and Duns Scotus developed many of their observations, it was C. I. Lewis who created the first symbolic and systematic approach to the topic, in 1912. It continued to mature as a field, reaching its modern form in 1963 with the work of Saul Kripke. Historical development Many papers were written in the 1950s that spoke of a logic of knowledge in passing, but the Finnish philosopher G. H. von Wright's 1951 paper titled ''An Essay in Modal Logic'' is seen as a founding document. It was not unti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Axiology
Value theory, also called ''axiology'', studies the nature, sources, and types of values. It is a branch of philosophy and an interdisciplinary field closely associated with social sciences such as economics, sociology, anthropology, and psychology. Value is the worth of something, usually understood as covering both positive and negative degrees corresponding to the terms '' good'' and ''bad''. Values influence many human endeavors related to emotion, decision-making, and action. Value theorists distinguish various types of values, like the contrast between intrinsic and instrumental value. An entity has intrinsic value if it is good in itself, independent of external factors. An entity has instrumental value if it is useful as a means leading to other good things. Other classifications focus on the type of benefit, including economic, moral, political, aesthetic, and religious values. Further categorizations distinguish absolute values from values that are relative to someth ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Deontic Logic
Deontic logic is the field of philosophical logic that is concerned with obligation, permission, and related concepts. Alternatively, a deontic logic is a formal system that attempts to capture the essential logical features of these concepts. It can be used to formalize imperative logic, or directive modality in natural languages. Typically, a deontic logic uses ''OA'' to mean ''it is obligatory that A'' (or ''it ought to be (the case) that A''), and ''PA'' to mean ''it is permitted (or permissible) that A'', which is defined as PA\equiv \neg O\neg A. In natural language, the statement "You may go to the zoo OR the park" should be understood as Pz\land Pp instead of Pz\lor Pp, as both options are permitted by the statement. When there are multiple agents involved in the domain of discourse, the deontic modal operator can be specified to each agent to express their individual obligations and permissions. For example, by using a subscript O_i for agent a_i, O_iA means that "It i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Alethic Modality
Alethic modality (from Greek ἀλήθεια = truth) is a linguistic modality that indicates modalities of truth, in particular the modalities of logical necessity, contingency, possibility and impossibility. Alethic modality is often associated with epistemic modality in research, and it has been questioned whether this modality should be considered distinct from epistemic modality which denotes the speaker's evaluation or judgment of the truth. The criticism states that there is no real difference between "the truth in the world" (alethic) and "the truth in an individual's mind" (epistemic). An investigation has not found a single language in which alethic and epistemic modalities would be formally distinguished, for example by the means of a grammatical mood. In such a language, "A circle can't be square", "can't be" would be expressed by an alethic mood, whereas for "He can't be that wealthy", "can't be" would be expressed by an epistemic mood. As we can see, this is not a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Interpretation (logic)
An interpretation is an assignment of meaning to the symbols of a formal language. Many formal languages used in mathematics, logic, and theoretical computer science are defined in solely syntactic terms, and as such do not have any meaning until they are given some interpretation. The general study of interpretations of formal languages is called formal semantics. The most commonly studied formal logics are propositional logic, predicate logic and their modal analogs, and for these there are standard ways of presenting an interpretation. In these contexts an interpretation is a function that provides the extension of symbols and strings of an object language. For example, an interpretation function could take the predicate symbol T and assign it the extension \. All our interpretation does is assign the extension \ to the non-logical symbol T, and does not make a claim about whether T is to stand for tall and \mathrm for Abraham Lincoln. On the other hand, an interpretation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |