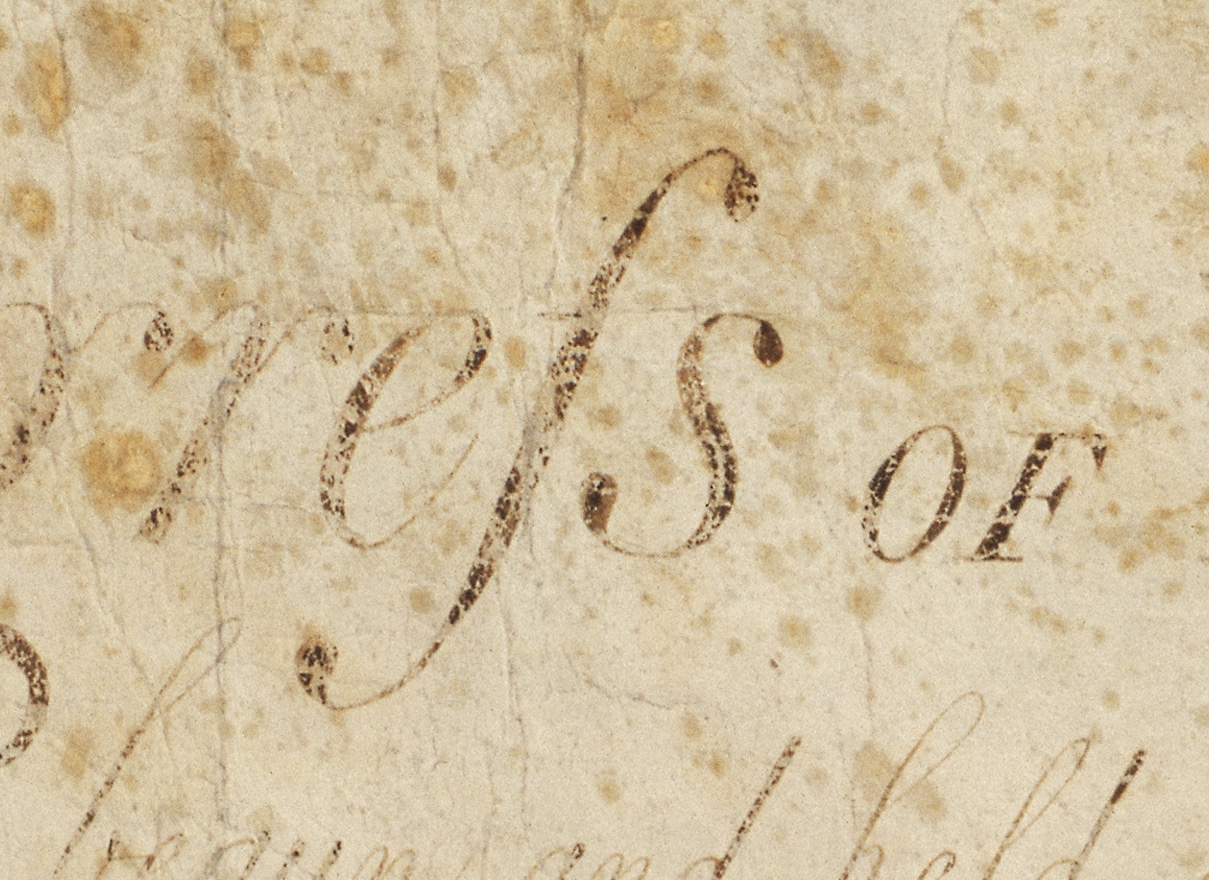|
Medial
Medial may refer to: Mathematics * Medial magma, a mathematical identity in algebra Geometry * Medial axis, in geometry the set of all points having more than one closest point on an object's boundary * Medial graph, another graph that represents the adjacencies between edges in the faces of a plane graph * Medial triangle, the triangle whose vertices lie at the midpoints of an enclosing triangle's sides * Polyhedra: ** Medial deltoidal hexecontahedron ** Medial disdyakis triacontahedron ** Medial hexagonal hexecontahedron ** Medial icosacronic hexecontahedron ** Medial inverted pentagonal hexecontahedron ** Medial pentagonal hexecontahedron ** Medial rhombic triacontahedron Linguistics * A medial sound or letter is one that is found in the middle of a larger unit (like a word) ** Syllable medial, a segment located between the onset and the rime of a syllable * In the older literature, a term for the voiced stops (like ''b'', ''d'', ''g'') * Medial or second person ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Medial Graph
In the mathematical discipline of graph theory, the medial graph of plane graph ''G'' is another graph ''M(G)'' that represents the adjacencies between edges in the faces of ''G''. Medial graphs were introduced in 1922 by Ernst Steinitz to study combinatorial properties of convex polyhedra, although the inverse construction was already used by Peter Tait in 1877 in his foundational study of knots and links. Formal definition Given a connected plane graph ''G'', its medial graph ''M(G)'' has * a vertex for each edge of ''G'' and * an edge between two vertices for each face of ''G'' in which their corresponding edges occur consecutively. The medial graph of a disconnected graph is the disjoint union of the medial graphs of each connected component. The definition of medial graph also extends without modification to graph embeddings Graph may refer to: Mathematics * Graph (discrete mathematics), a structure made of vertices and edges ** Graph theory, the study of such graphs ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Medial Magma
In abstract algebra, a medial magma or medial groupoid is a magma or groupoid (that is, a set with a binary operation) which satisfies the identity :(x \cdot y) \cdot (u \cdot v) = (x \cdot u) \cdot (y \cdot v), or more simply xy\cdot uv = xu\cdot yv for all ''x'', ''y'', ''u'' and ''v'', using the convention that juxtaposition denotes the same operation but has higher precedence. This identity has been variously called ''medial'', ''abelian'', ''alternation'', ''transposition'', ''interchange'', ''bi-commutative'', ''bisymmetric'', ''surcommutative'', ''entropic'' etc.Historical comments J.Jezek and T.Kepka: Medial groupoids Rozpravy CSAV, Rada mat. a prir. ved 93/2 (1983), 93 pp Any ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Medial Triangle
In Euclidean geometry, the medial triangle or midpoint triangle of a triangle is the triangle with vertices at the midpoints of the triangle's sides . It is the case of the midpoint polygon of a polygon with sides. The medial triangle is not the same thing as the median triangle, which is the triangle whose sides have the same lengths as the medians of . Each side of the medial triangle is called a ''midsegment'' (or ''midline''). In general, a midsegment of a triangle is a line segment which joins the midpoints of two sides of the triangle. It is parallel to the third side and has a length equal to half the length of the third side. Properties The medial triangle can also be viewed as the image of triangle transformed by a homothety centered at the centroid with ratio -1/2. Thus, the sides of the medial triangle are half and parallel to the corresponding sides of triangle ABC. Hence, the medial triangle is inversely similar and shares the same centroid and medians ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Medial Axis
The medial axis of an object is the set of all points having more than one closest point on the object's boundary. Originally referred to as the topological skeleton, it was introduced in 1967 by Harry Blum as a tool for biological shape recognition. In mathematics the closure of the medial axis is known as the cut locus. In 2D, the medial axis of a subset ''S'' which is bounded by planar curve ''C'' is the locus of the centers of circles that are tangent to curve ''C'' in two or more points, where all such circles are contained in ''S''. (It follows that the medial axis itself is contained in ''S''.) The medial axis of a simple polygon is a tree whose leaves are the vertices of the polygon, and whose edges are either straight segments or arcs of parabolas. The medial axis together with the associated radius function of the maximally inscribed discs is called the medial axis transform (MAT). The medial axis transform is a complete shape descriptor (see also shape analysi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Medial Capitals
Camel case (sometimes stylized as camelCase or CamelCase, also known as camel caps or more formally as medial capitals) is the practice of writing phrases without spaces or punctuation. The format indicates the separation of words with a single capitalized letter, and the first word starting with either case. Common examples include " iPhone" and "eBay". It is also sometimes used in online usernames such as "johnSmith", and to make multi-word domain names more legible, for example in promoting "EasyWidgetCompany.com". Camel case is often used as a naming convention in computer programming, but is an ambiguous definition due to the optional capitalization of the first letter. Some programming styles prefer camel case with the first letter capitalised, others not. For clarity, this article calls the two alternatives upper camel case (initial uppercase letter, also known as Pascal case or bumpy case) and lower camel case (initial lowercase letter, also known as dromedary case). Some ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
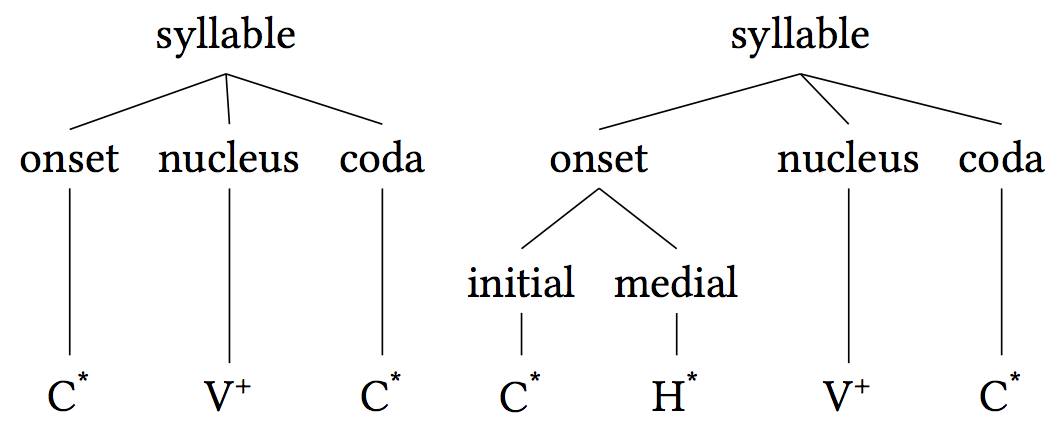
Syllable Medial
A syllable is a unit of organization for a sequence of speech sounds typically made up of a syllable nucleus (most often a vowel) with optional initial and final margins (typically, consonants). Syllables are often considered the phonological "building blocks" of words. They can influence the rhythm of a language, its prosody, its poetic metre and its stress patterns. Speech can usually be divided up into a whole number of syllables: for example, the word ''ignite'' is made of two syllables: ''ig'' and ''nite''. Syllabic writing began several hundred years before the first letters. The earliest recorded syllables are on tablets written around 2800 BC in the Sumerian city of Ur. This shift from pictograms to syllables has been called "the most important advance in the history of writing". A word that consists of a single syllable (like English ''dog'') is called a monosyllable (and is said to be ''monosyllabic''). Similar terms include disyllable (and ''disyllabic''; ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Medial Rhombic Triacontahedron
__NOTOC__ In geometry, the medial rhombic triacontahedron (or midly rhombic triacontahedron) is a nonconvex isohedral polyhedron. It is a stellation of the rhombic triacontahedron, and can also be called small stellated triacontahedron. Its dual is the dodecadodecahedron. Its 24 vertices are all on the 12 axes with 5-fold symmetry (i.e. each corresponds to one of the 12 vertices of the icosahedron). This means that on each axis there is an inner and an outer vertex. The ratio of outer to inner vertex radius is \varphi \approx 1.618, the golden ratio. It has 30 intersecting rhombic faces, which correspond to the faces of the convex rhombic triacontahedron. The diagonals in the rhombs of the convex solid have a ratio of 1 to \varphi. The medial solid can be generated from the convex one by stretching the shorter diagonal from length 1 to \varphi^3 \approx 4.236. So the ratio of rhomb diagonals in the medial solid is 1 to \varphi^2 \approx 2.618. This solid is to the compound of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Medial (anatomy)
Standard anatomical terms of location are used to unambiguously describe the anatomy of animals, including humans. The terms, typically derived from Latin or Greek roots, describe something in its standard anatomical position. This position provides a definition of what is at the front ("anterior"), behind ("posterior") and so on. As part of defining and describing terms, the body is described through the use of anatomical planes and anatomical axes. The meaning of terms that are used can change depending on whether an organism is bipedal or quadrupedal. Additionally, for some animals such as invertebrates, some terms may not have any meaning at all; for example, an animal that is radially symmetrical will have no anterior surface, but can still have a description that a part is close to the middle ("proximal") or further from the middle ("distal"). International organisations have determined vocabularies that are often used as standard vocabularies for subdisciplines of anatom ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Medial S
The long s , also known as the medial s or initial s, is an archaic form of the lowercase letter . It replaced the single ''s'', or one or both of the letters ''s'' in a 'double ''s''' sequence (e.g., "ſinfulneſs" for "sinfulness" and "poſſeſs" or "poſseſs" for "possess"—but never *"poſſeſſ"). The modern letterform is known as the 'short', 'terminal', or 'round' s. In typography, it is known as a type of swash letter, commonly referred to as a "swash s". The long s is the basis of the first half of the grapheme of the German alphabet ligature letter , ('' eszett'' or harp s. Rules This list of rules for the long s is not exhaustive, and it applies only to books printed during the 17th and 18th centuries in English-speaking countries. Similar rules exist for other European languages. * A round s is always used at the end of a word ending with s: "his", "complains", "ſucceſs" ** However, long s is maintained in abbreviations such as "ſ." for "ſubſtantiv ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Medial Inverted Pentagonal Hexecontahedron
In geometry, the inverted snub dodecadodecahedron (or vertisnub dodecadodecahedron) is a nonconvex uniform polyhedron, indexed as U60. It is given a Schläfli symbol sr. Cartesian coordinates Cartesian coordinates for the vertices of an inverted snub dodecadodecahedron are all the even permutations of : (±2α, ±2, ±2β), : (±(α+β/τ+τ), ±(-ατ+β+1/τ), ±(α/τ+βτ-1)), : (±(-α/τ+βτ+1), ±(-α+β/τ-τ), ±(ατ+β-1/τ)), : (±(-α/τ+βτ-1), ±(α-β/τ-τ), ±(ατ+β+1/τ)) and : (±(α+β/τ-τ), ±(ατ-β+1/τ), ±(α/τ+βτ+1)), with an even number of plus signs, where : β = (α2/τ+τ)/(ατ−1/τ), where τ = (1+)/2 is the golden mean and α is the negative real root of τα4−α3+2α2−α−1/τ, or approximately −0.3352090. Taking the odd permutations of the above coordinates with an odd number of plus signs gives another form, the enantiomorph of the other one. Related polyhedra Medial inverted pentagonal hexecontahedron The medial ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Medial Hexagonal Hexecontahedron
In geometry, the medial hexagonal hexecontahedron (or midly dentoid ditriacontahedron) is a nonconvex Isohedral figure, isohedral polyhedron. It is the Dual polyhedron, dual of the uniform star polyhedron, uniform snub icosidodecadodecahedron. Proportions The faces of the medial hexagonal hexecontahedron are irregular nonconvex hexagons. Denote the golden ratio by \phi, and let \xi\approx -0.377\,438\,833\,12 be the real zero of the polynomial 8x^3-4x^2+1. The number \xi can be written as \xi=-1/(2\rho), where \rho is the plastic number. Then each face has four equal angles of \arccos(\xi)\approx 112.175\,128\,045\,27^, one of \arccos(\phi^2\xi+\phi)\approx 50.958\,265\,917\,31^ and one of 360^-\arccos(\phi^\xi-\phi^)\approx 220.341\,221\,901\,59^. Each face has two long edges, two of medium length and two short ones. If the medium edges have length 2, the long ones have length 1+\sqrt\approx 4.121\,448\,816\,41 and the short ones 1-\sqrt\approx 0.453\,587\,559\,98. The dihedral ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Medial Pentagonal Hexecontahedron
In geometry, the medial pentagonal hexecontahedron is a nonconvex isohedral polyhedron. It is the dual of the snub dodecadodecahedron. It has 60 intersecting irregular pentagonal faces. Proportions Denote the golden ratio by \phi, and let \xi\approx -0.409\,037\,788\,014\,42 be the smallest (most negative) real zero of the polynomial P=8x^4-12x^3+5x+1. Then each face has three equal angles of \arccos(\xi)\approx 114.144\,404\,470\,43^, one of \arccos(\phi^2\xi+\phi)\approx 56.827\,663\,280\,94^ and one of \arccos(\phi^\xi-\phi^)\approx 140.739\,123\,307\,76^. Each face has one medium length edge, two short and two long ones. If the medium length is 2, then the short edges have length :1+\sqrt\approx 1.550\,761\,427\,20, and the long edges have length :1+\sqrt\approx 3.854\,145\,870\,08. The dihedral angle A dihedral angle is the angle between two intersecting planes or half-planes. In chemistry, it is the clockwise angle between half-planes through two sets of three atoms ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |