|
Maximum Disjoint Set
In computational geometry, a maximum disjoint set (MDS) is a largest set of non-overlapping geometric shapes selected from a given set of candidate shapes. Every set of non-overlapping shapes is an independent set (graph theory), independent set in the intersection graph of the shapes. Therefore, the MDS problem is a special case of the maximum independent set (MIS) problem. Both problems are NP complete, but finding a MDS may be easier than finding a MIS in two respects: * For the general MIS problem, the best known exact algorithms are exponential. In some geometric intersection graphs, there are sub-exponential algorithms for finding a MDS. * The general MIS problem is hard to approximate and doesn't even have a constant-factor approximation. In some geometric intersection graphs, there are polynomial-time approximation schemes (PTAS) for finding a MDS. Finding an MDS is important in applications such as automatic label placement, VLSI circuit design, and cellular frequency divi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Discrete & Computational Geometry
'' Discrete & Computational Geometry'' is a peer-reviewed mathematics journal published quarterly by Springer. Founded in 1986 by Jacob E. Goodman and Richard M. Pollack, the journal publishes articles on discrete geometry and computational geometry. Abstracting and indexing The journal is indexed in: * ''Mathematical Reviews'' * '' Zentralblatt MATH'' * ''Science Citation Index'' * ''Current Contents ''Current Contents'' is a rapid alerting service database from Clarivate, formerly the Institute for Scientific Information and Thomson Reuters. It is published online and in several different printed subject sections. History ''Current Contents ...'' Notable articles Two articles published in ''Discrete & Computational Geometry'', one by Gil Kalai in 1992 with a proof of a subexponential upper bound on the diameter of a polytope and another by Samuel Ferguson in 2006 on the Kepler conjecture on optimal three-dimensional sphere packing, earned their authors the Fulk ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Local Search Algorithm
In computer science, local search is a heuristic method for solving computationally hard optimization problems. Local search can be used on problems that can be formulated as finding a solution that maximizes a criterion among a number of candidate solutions. Local search algorithms move from solution to solution in the space of candidate solutions (the ''search space'') by applying local changes, until a solution deemed optimal is found or a time bound is elapsed. Local search algorithms are widely applied to numerous hard computational problems, including problems from computer science (particularly artificial intelligence), mathematics, operations research, engineering, and bioinformatics. Examples of local search algorithms are WalkSAT, the 2-opt algorithm for the Traveling Salesman Problem and the Metropolis–Hastings algorithm. While it is sometimes possible to substitute gradient descent for a local search algorithm, gradient descent is not in the same family: although ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Union Complexity
Union commonly refers to: * Trade union, an organization of workers * Union (set theory), in mathematics, a fundamental operation on sets Union may also refer to: Arts and entertainment Music * Union (band), an American rock group ** ''Union'' (Union album), 1998 * ''Union'' (Chara album), 2007 * ''Union'' (Toni Childs album), 1988 * ''Union'' (Cuff the Duke album), 2012 * ''Union'' (Paradoxical Frog album), 2011 * ''Union'', a 2001 album by Puya * ''Union'', a 2001 album by Rasa * ''Union'' (Son Volt album), 2019 * ''Union'' (The Boxer Rebellion album), 2009 * ''Union'' (Yes album), 1991 * "Union" (Black Eyed Peas song), 2005 Other uses in arts and entertainment * ''Union'' (film), a labor documentary released in 2024 * ''Union'' (Star Wars), a Dark Horse comics limited series * Union, in the fictional Alliance–Union universe of C. J. Cherryh * ''Union (Horse with Two Discs)'', a bronze sculpture by Christopher Le Brun, 1999–2000 * The Union (Marvel Team), a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometric Separator
A geometric separator is a line (or another shape) that partitions a collection of geometric shapes into two subsets, such that proportion of shapes in each subset is bounded, and the number of shapes that do not belong to any subset (i.e. the shapes intersected by the separator itself) is small. When a geometric separator exists, it can be used for building divide-and-conquer algorithms for solving various problems in computational geometry. Separators that are lines General question In 1979, Helge Tverberg raised the following question. For two positive integers ''k'', ''l'', what is the smallest number ''n''(''k'',''l'') such that, for any family of pairwise-disjoint convex objects in the plane, there exists a straight line that has at least ''k'' objects on one side and at least ''l'' on the other side? The following results are known. * Obviously, ''n''(1,1)=1. * Hope and Katchalski proved that ''n''(''k'',1) ≤ 12(''k''-1) for all ''k'' ≥ 2. * Villanger prov ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quadtree
A quadtree is a tree data structure in which each internal node has exactly four children. Quadtrees are the two-dimensional analog of octrees and are most often used to partition a two-dimensional space by recursively subdividing it into four quadrants or regions. The data associated with a leaf cell varies by application, but the leaf cell represents a "unit of interesting spatial information". The subdivided regions may be square or rectangular, or may have arbitrary shapes. This data structure was named a quadtree by Raphael Finkel and J.L. Bentley in 1974. A similar partitioning is also known as a ''Q-tree''. All forms of quadtrees share some common features: * They decompose space into adaptable cells. * Each cell (or bucket) has a maximum capacity. When maximum capacity is reached, the bucket splits. * The tree directory follows the spatial decomposition of the quadtree. A tree-pyramid (T-pyramid) is a "complete" tree; every node of the T-pyramid has four child nodes e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Point Quadtree
A point is a small dot or the sharp tip of something. Point or points may refer to: Mathematics * Point (geometry), an entity that has a location in space or on a plane, but has no extent; more generally, an element of some abstract topological space * Point, or Element (category theory), generalizes the set-theoretic concept of an element of a set to an object of any category * Critical point (mathematics), a stationary point of a function of an arbitrary number of variables * Decimal point * Point-free geometry * Stationary point, a point in the domain of a single-valued function where the value of the function ceases to change Places * Point, Cornwall, England, a settlement in Feock parish * Point, Lewis, a peninsula in the Outer Hebrides, Scotland * Point, Texas, a city in Rains County, Texas, United States * Point, the NE tip and a ferry terminal of Lismore, Inner Hebrides, Scotland * Points, West Virginia, an unincorporated community in the United States Business an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pigeonhole Principle
In mathematics, the pigeonhole principle states that if items are put into containers, with , then at least one container must contain more than one item. For example, of three gloves, at least two must be right-handed or at least two must be left-handed, because there are three objects but only two categories of handedness to put them into. This seemingly obvious statement, a type of combinatorics, counting argument, can be used to demonstrate possibly unexpected results. For example, given that the Demographics of London, population of London is more than one unit greater than the maximum number of hairs that can be on a human's head, the principle requires that there must be at least two people in London who have the same number of hairs on their heads. Although the pigeonhole principle appears as early as 1624 in a book attributed to Jean Leurechon, it is commonly called Dirichlet's box principle or Dirichlet's drawer principle after an 1834 treatment of the principle by Pet ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
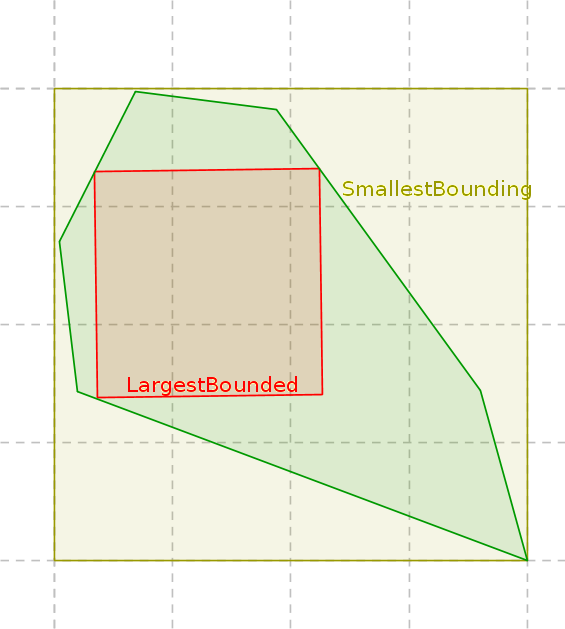
Fat Object (geometry)
In geometry, a fat object is an object in two or more dimensions, whose lengths in the different dimensions are similar. For example, a square is fat because its length and width are identical. A 2-by-1 rectangle is thinner than a square, but it is fat relative to a 10-by-1 rectangle. Similarly, a circle is fatter than a 1-by-10 ellipse and an equilateral triangle is fatter than a very obtuse triangle. Fat objects are especially important in computational geometry. Many algorithms in computational geometry can perform much better if their input consists of only fat objects; see the #Applications, applications section below. Global fatness Given a constant , an object is called -fat if its "slimness factor" is at most . The "slimness factor" has different definitions in different papers. A common definition is: :\frac where and the cubes are -dimensional. A 2-dimensional cube is a square, so the slimness factor of a square is 1 (since its smallest enclosing square is the sam ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Circles
A circle is a shape consisting of all points in a plane that are at a given distance from a given point, the centre. The distance between any point of the circle and the centre is called the radius. The length of a line segment connecting two points on the circle and passing through the centre is called the diameter. A circle bounds a region of the plane called a disc. The circle has been known since before the beginning of recorded history. Natural circles are common, such as the full moon or a slice of round fruit. The circle is the basis for the wheel, which, with related inventions such as gears, makes much of modern machinery possible. In mathematics, the study of the circle has helped inspire the development of geometry, astronomy and calculus. Terminology * Annulus: a ring-shaped object, the region bounded by two concentric circles. * Arc: any connected part of a circle. Specifying two end points of an arc and a centre allows for two arcs that together make up ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |