|
Maximally Informative Dimensions
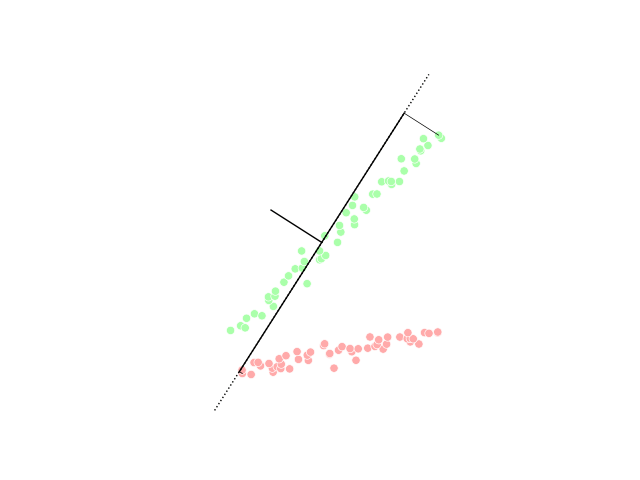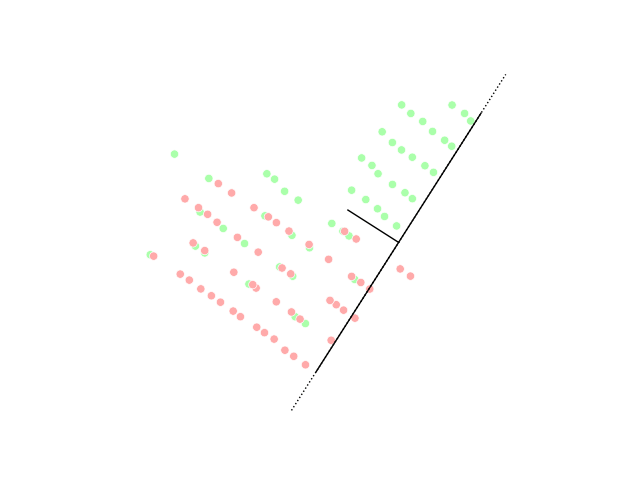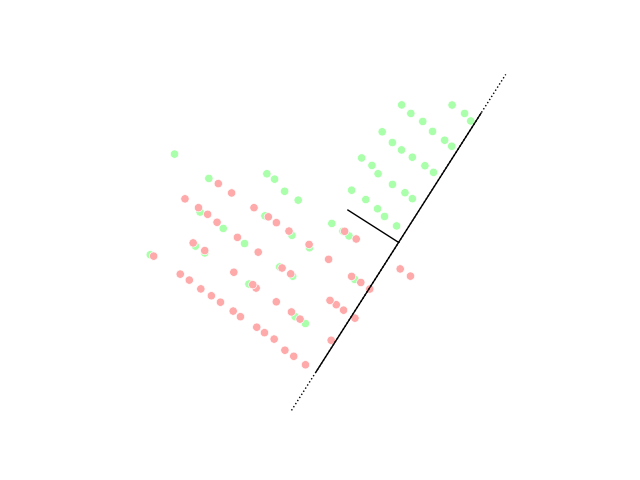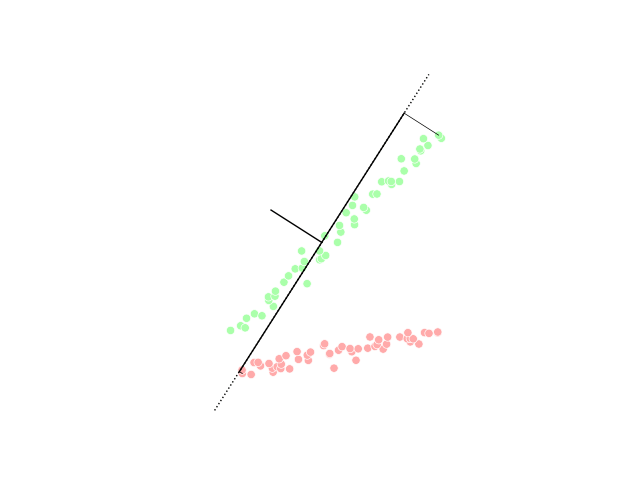
Maximally informative dimensions is a dimensionality reduction technique used in the statistical analyses of neural responses. Specifically, it is a way of projecting a stimulus onto a low-dimensional subspace so that as much information as possible about the stimulus is preserved in the neural response. It is motivated by the fact that natural stimuli are typically confined by their statistics to a lower-dimensional space than that spanned by white noise but correctly identifying this subspace using traditional techniques is complicated by the correlations that exist within natural images. Within this subspace, stimulus-response functions may be either linear or nonlinear. The idea was originally developed by Tatyana Sharpee, Nicole C. Rust, and William Bialek in 2003. Mathematical formulation Neural stimulus-response functions are typically given as the probability of a neuron generating an action potential, or spike, in response to a stimulus \mathbf. The goal of maximally ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dimensionality Reduction
Dimensionality reduction, or dimension reduction, is the transformation of data from a high-dimensional space into a low-dimensional space so that the low-dimensional representation retains some meaningful properties of the original data, ideally close to its intrinsic dimension. Working in high-dimensional spaces can be undesirable for many reasons; raw data are often sparse as a consequence of the curse of dimensionality, and analyzing the data is usually computationally intractable (hard to control or deal with). Dimensionality reduction is common in fields that deal with large numbers of observations and/or large numbers of variables, such as signal processing, speech recognition, neuroinformatics, and bioinformatics. Methods are commonly divided into linear and nonlinear approaches. Approaches can also be divided into feature selection and feature extraction. Dimensionality reduction can be used for noise reduction, data visualization, cluster analysis, or as an interme ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
William Bialek
William Samuel Bialek (born 1960, in Los Angeles, California) is a theoretical biophysicist and a professor at Princeton University and The Graduate Center, CUNY. Much of his work, which has ranged over a wide variety of theoretical problems at the interface of physics and biology, centers around whether various functions of living beings are optimal, and (if so) whether a precise quantification of their performance approaches limits set by basic physical principles. Best known among these is an influential series of studies applying the principles of information theory to the analysis of the neural encoding of information in the nervous system, showing that aspects of brain function can be described as essentially optimal strategies for adapting to the complex dynamics of the world, making the most of the available signals in the face of fundamental physical constraints and limitations. Bialek received his AB (1979) and PhD (1983) degrees in Biophysics from the University of Cali ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spike-triggered Covariance
Spike-triggered covariance (STC) analysis is a tool for characterizing a neuron's response properties using the covariance of stimuli that elicit spikes from a neuron. STC is related to the spike-triggered average (STA), and provides a complementary tool for estimating linear filters in a linear-nonlinear-Poisson (LNP) cascade model. Unlike STA, the STC can be used to identify a multi-dimensional feature space in which a neuron computes its response. STC analysis identifies the stimulus features affecting a neuron's response via an eigenvector decomposition of the spike-triggered covariance matrix.Brenner, N., Bialek, W., & de Ruyter van Steveninck, R.R. (2000). Schwartz, O., Chichilnisky, E. J., & Simoncelli, E. P. (2002). Bialek, W. & de Ruyter van Steveninck, R. (2005). Arxiv preprint q-bio/0505003.Schwartz O., Pillow J. W., Rust N. C., & Simoncelli E. P. (2006). Spike-triggered neural characterization. ''Journal of Vision'' 6:484-507 Eigenvectors with eigenvalues significant ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Normal Distribution
In statistics, a normal distribution or Gaussian distribution is a type of continuous probability distribution for a real-valued random variable. The general form of its probability density function is : f(x) = \frac e^ The parameter \mu is the mean or expectation of the distribution (and also its median and mode), while the parameter \sigma is its standard deviation. The variance of the distribution is \sigma^2. A random variable with a Gaussian distribution is said to be normally distributed, and is called a normal deviate. Normal distributions are important in statistics and are often used in the natural and social sciences to represent real-valued random variables whose distributions are not known. Their importance is partly due to the central limit theorem. It states that, under some conditions, the average of many samples (observations) of a random variable with finite mean and variance is itself a random variable—whose distribution converges to a normal dist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dirac Delta Function
In mathematics, the Dirac delta distribution ( distribution), also known as the unit impulse, is a generalized function or distribution over the real numbers, whose value is zero everywhere except at zero, and whose integral over the entire real line is equal to one. The current understanding of the unit impulse is as a linear functional that maps every continuous function (e.g., f(x)) to its value at zero of its domain (f(0)), or as the weak limit of a sequence of bump functions (e.g., \delta(x) = \lim_ \frace^), which are zero over most of the real line, with a tall spike at the origin. Bump functions are thus sometimes called "approximate" or "nascent" delta distributions. The delta function was introduced by physicist Paul Dirac as a tool for the normalization of state vectors. It also has uses in probability theory and signal processing. Its validity was disputed until Laurent Schwartz developed the theory of distributions where it is defined as a linear form acting o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mean
There are several kinds of mean in mathematics, especially in statistics. Each mean serves to summarize a given group of data, often to better understand the overall value ( magnitude and sign) of a given data set. For a data set, the '' arithmetic mean'', also known as "arithmetic average", is a measure of central tendency of a finite set of numbers: specifically, the sum of the values divided by the number of values. The arithmetic mean of a set of numbers ''x''1, ''x''2, ..., x''n'' is typically denoted using an overhead bar, \bar. If the data set were based on a series of observations obtained by sampling from a statistical population, the arithmetic mean is the '' sample mean'' (\bar) to distinguish it from the mean, or expected value, of the underlying distribution, the '' population mean'' (denoted \mu or \mu_x).Underhill, L.G.; Bradfield d. (1998) ''Introstat'', Juta and Company Ltd.p. 181/ref> Outside probability and statistics, a wide range of other notions of m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bayes' Theorem
In probability theory and statistics, Bayes' theorem (alternatively Bayes' law or Bayes' rule), named after Thomas Bayes, describes the probability of an event, based on prior knowledge of conditions that might be related to the event. For example, if the risk of developing health problems is known to increase with age, Bayes' theorem allows the risk to an individual of a known age to be assessed more accurately (by conditioning it on their age) than simply assuming that the individual is typical of the population as a whole. One of the many applications of Bayes' theorem is Bayesian inference, a particular approach to statistical inference. When applied, the probabilities involved in the theorem may have different probability interpretations. With Bayesian probability interpretation, the theorem expresses how a degree of belief, expressed as a probability, should rationally change to account for the availability of related evidence. Bayesian inference is fundamental to Baye ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Projection (mathematics)
In mathematics, a projection is a mapping of a set (or other mathematical structure) into a subset (or sub-structure), which is equal to its square for mapping composition, i.e., which is idempotent. The restriction to a subspace of a projection is also called a ''projection'', even if the idempotence property is lost. An everyday example of a projection is the casting of shadows onto a plane (sheet of paper): the projection of a point is its shadow on the sheet of paper, and the projection (shadow) of a point on the sheet of paper is that point itself (idempotency). The shadow of a three-dimensional sphere is a closed disk. Originally, the notion of projection was introduced in Euclidean geometry to denote the projection of the three-dimensional Euclidean space onto a plane in it, like the shadow example. The two main projections of this kind are: * The projection from a point onto a plane or central projection: If ''C'' is a point, called the center of projection, then th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
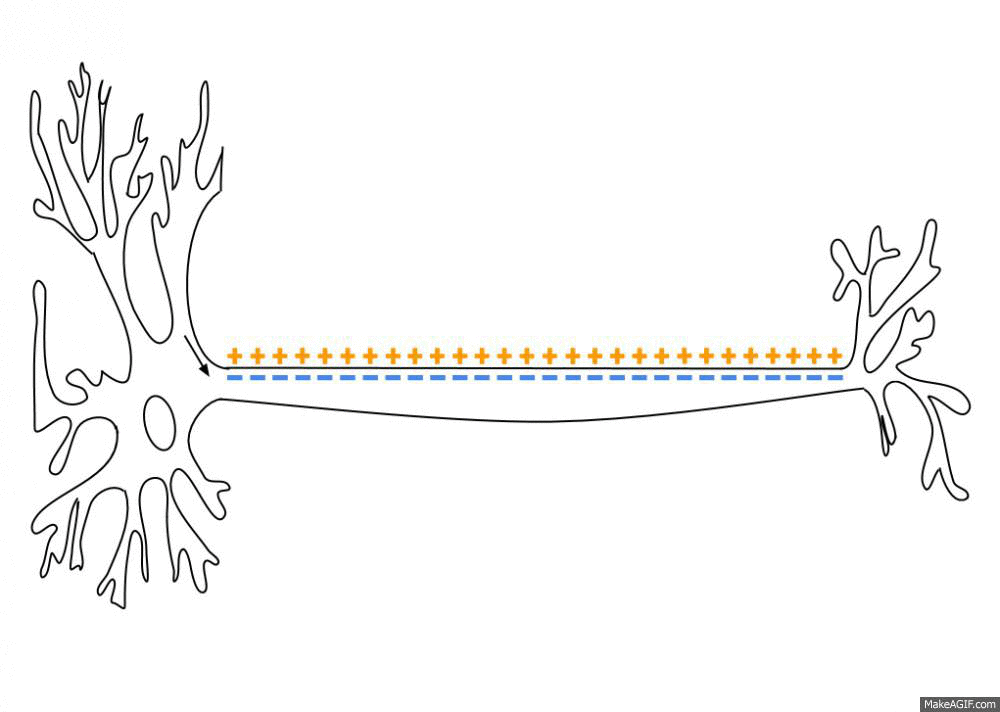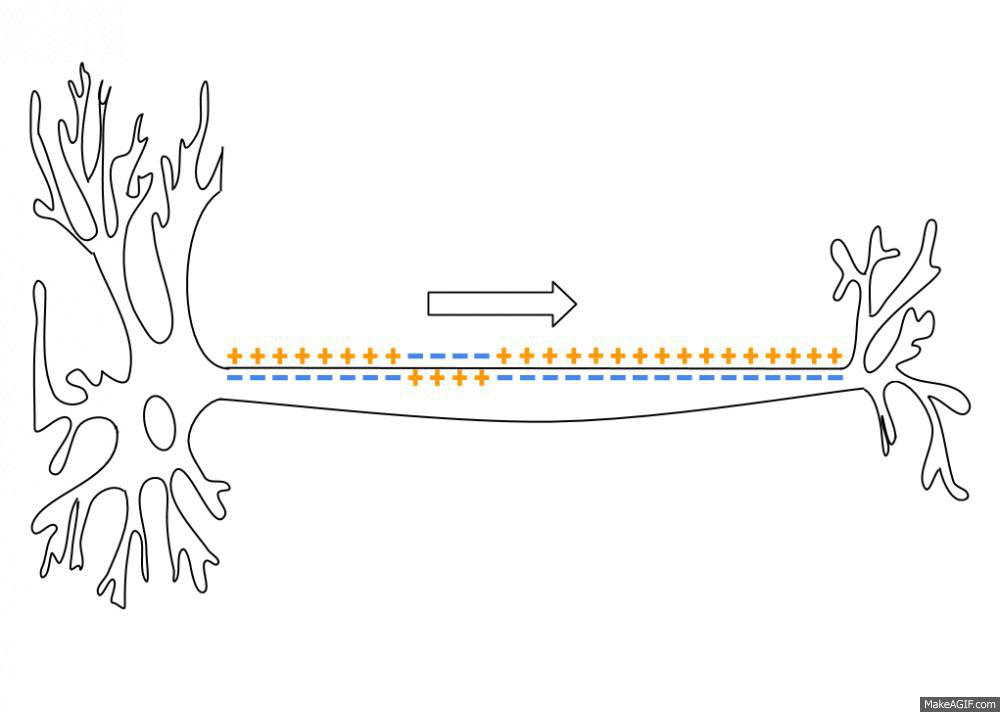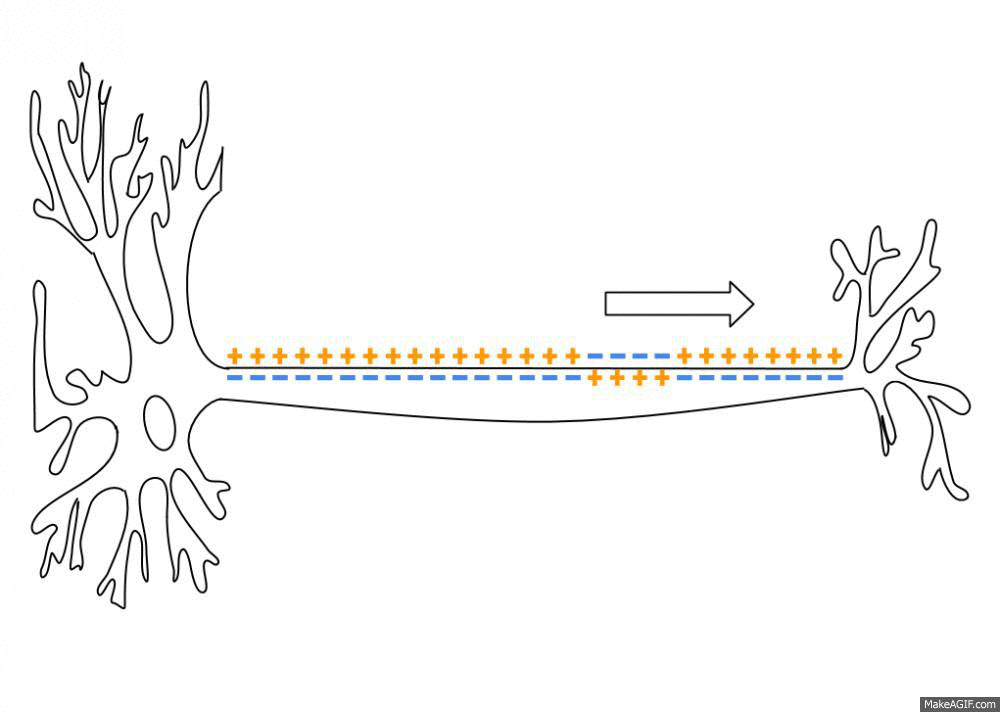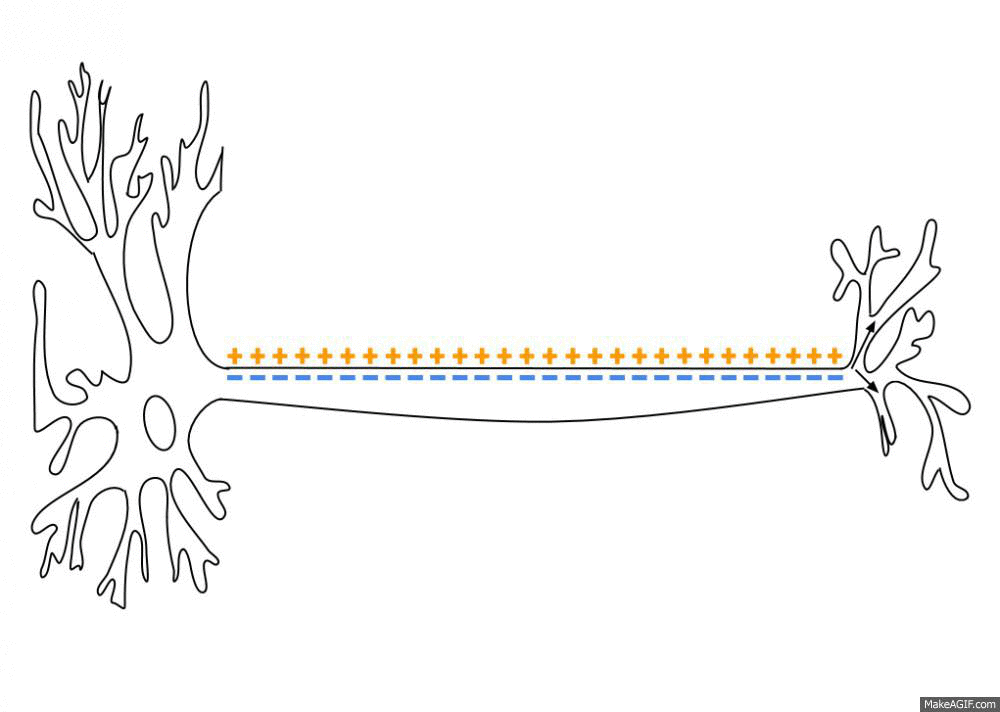
Action Potential
An action potential occurs when the membrane potential of a specific cell location rapidly rises and falls. This depolarization then causes adjacent locations to similarly depolarize. Action potentials occur in several types of animal cells, called excitable cells, which include neurons, muscle cells, and in some plant cells. Certain endocrine cells such as pancreatic beta cells, and certain cells of the anterior pituitary gland are also excitable cells. In neurons, action potentials play a central role in cell-cell communication by providing for—or with regard to saltatory conduction, assisting—the propagation of signals along the neuron's axon toward synaptic boutons situated at the ends of an axon; these signals can then connect with other neurons at synapses, or to motor cells or glands. In other types of cells, their main function is to activate intracellular processes. In muscle cells, for example, an action potential is the first step in the chain of event ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Neuron
A neuron, neurone, or nerve cell is an membrane potential#Cell excitability, electrically excitable cell (biology), cell that communicates with other cells via specialized connections called synapses. The neuron is the main component of nervous tissue in all Animalia, animals except sponges and placozoa. Non-animals like plants and fungi do not have nerve cells. Neurons are typically classified into three types based on their function. Sensory neurons respond to Stimulus (physiology), stimuli such as touch, sound, or light that affect the cells of the Sense, sensory organs, and they send signals to the spinal cord or brain. Motor neurons receive signals from the brain and spinal cord to control everything from muscle contractions to gland, glandular output. Interneurons connect neurons to other neurons within the same region of the brain or spinal cord. When multiple neurons are connected together, they form what is called a neural circuit. A typical neuron consists of a cell bo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nicole C
Nicole may refer to: People * Nicole (name) * Nicole (American singer) (born 1958), a contestant in season 3 of the American ''The X Factor'' * Nicole (Chilean singer) (born 1977) * Nicole (German singer) (born 1964), winner of the 1982 Eurovision Song Contest * Nicole, Countess of Penthièvre (c. 1424–after 1480) * Nicole, Duchess of Lorraine (1608–1657), French noblewoman * Nicole LaRoche, flutist in the band Brulé, releases solo albums as "Nicole" Storms * Tropical Storm Nicole, a number of named tropical and subtropical cyclones ** Tropical Storm Nicole (2010) ** Hurricane Nicole (2016) ** Hurricane Nicole (2022) Other uses * ''Nicole'' (film), a 1978 thriller * ''Nicole'' (video game), a visual novel style game * Nicole, Lot-et-Garonne, a town in France * “Nicole”, a song by Ween from the 1990 album '' GodWeenSatan: The Oneness'' * ''Nicole'' (album), an album by Indonesian singer NIKI See also * Nicolle * Nicoll Highway * Nichole * Nicholas ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Neural Coding
Neural coding (or Neural representation) is a neuroscience field concerned with characterising the hypothetical relationship between the Stimulus (physiology), stimulus and the individual or Neuronal ensemble, ensemble neuronal responses and the relationship among the Electrophysiology, electrical activity of the neurons in the ensemble. Based on the theory that sensory and other information is represented in the brain by Biological neural network, networks of neurons, it is thought that neurons can encode both Digital data, digital and analog signal, analog information. Overview Neurons are remarkable among the cells (biology), cells of the body in their ability to propagate signals rapidly over large distances. They do this by generating characteristic electrical pulses called action potentials: voltage spikes that can travel down axons. Sensory neurons change their activities by firing sequences of action potentials in various temporal patterns, with the presence of external se ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |