|
Materials Simulation
Computational materials science and engineering uses modeling, simulation, theory, and informatics to understand materials. The main goals include discovering new materials, determining material behavior and mechanisms, explaining experiments, and exploring materials theories. It is analogous to computational chemistry and computational biology as an increasingly important subfield of materials science. Introduction Just as materials science spans all length scales, from electrons to components, so do its computational sub-disciplines. While many methods and variations have been and continue to be developed, seven main simulation techniques, or motifs, have emerged. These computer simulation methods use underlying models and approximations to understand material behavior in more complex scenarios than pure theory generally allows and with more detail and precision than is often possible from experiments. Each method can be used independently to predict materials properties and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Informatics
Informatics is the study of computational systems. According to the Association for Computing Machinery, ACM Europe Council and Informatics Europe, informatics is synonymous with computer science and computing as a profession, in which the central notion is Data processing, transformation of information. In some cases, the term "informatics" may also be used with different meanings, e.g., in the context of social computing or library science. Different meanings In some countries, depending on local interpretations and contexts, the term "informatics" is used synonymously to mean information systems, information science, information theory, information engineering, information technology, information processing, or other theoretical or practical fields. In Germany, the term ''informatics'' closely corresponds to modern computer science. Accordingly, universities in continental Europe usually translate "informatics" as computer science, or sometimes information and computer sci ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
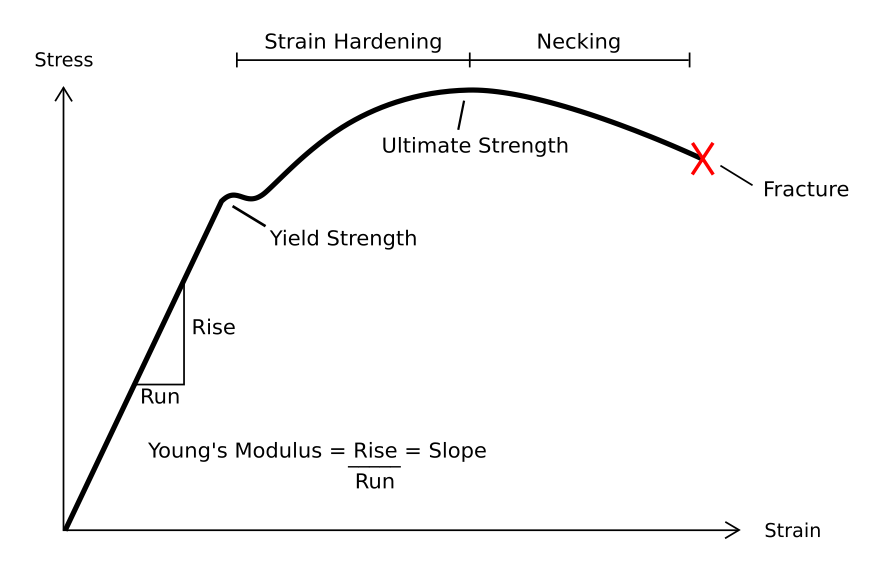
Plastic Deformation
In engineering, deformation (the change in size or shape of an object) may be ''elastic'' or ''plastic''. If the deformation is negligible, the object is said to be ''rigid''. Main concepts Occurrence of deformation in engineering applications is based on the following background concepts: * ''Displacements'' are any change in position of a point on the object, including whole-body translations and rotations ( rigid transformations). * ''Deformation'' are changes in the relative position between internals points on the object, excluding rigid transformations, causing the body to change shape or size. * ''Strain'' is the ''relative'' ''internal'' deformation, the dimensionless change in shape of an infinitesimal cube of material relative to a reference configuration. Mechanical strains are caused by mechanical stress, ''see stress-strain curve''. The relationship between stress and strain is generally linear and reversible up until the yield point and the deformation is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Monte Carlo
Monte Carlo ( ; ; or colloquially ; , ; ) is an official administrative area of Monaco, specifically the Ward (country subdivision), ward of Monte Carlo/Spélugues, where the Monte Carlo Casino is located. Informally, the name also refers to a larger district, the Monte Carlo Quarter (corresponding to the former municipality of Monte Carlo), which besides Monte Carlo/Spélugues also includes the wards of Saint Roman, Monaco, La Rousse/Saint Roman, Larvotto, Larvotto/Bas Moulins and Saint Michel, Monaco, Saint Michel. The permanent population of the ward of Monte Carlo is about 3,500, while that of the quarter is about 15,000. Monaco has four traditional quarters, from west to east they are: Fontvieille, Monaco, Fontvieille (the newest), Monaco City, Monaco-Ville (the oldest), La Condamine, and Monte Carlo. Monte Carlo is situated on a prominent escarpment at the base of the Maritime Alps along the French Riviera. Near the quarter's western end is the "world-famous Place du Ca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Potts Model
In statistical mechanics, the Potts model, a generalization of the Ising model, is a model of interacting spins on a crystalline lattice. By studying the Potts model, one may gain insight into the behaviour of ferromagnets and certain other phenomena of solid-state physics. The strength of the Potts model is not so much that it models these physical systems well; it is rather that the one-dimensional case is exactly solvable, and that it has a rich mathematical formulation that has been studied extensively. The model is named after Renfrey Potts, who described the model near the end of his 1951 Ph.D. thesis. The model was related to the "planar Potts" or " clock model", which was suggested to him by his advisor, Cyril Domb. The four-state Potts model is sometimes known as the Ashkin–Teller model, after Julius Ashkin and Edward Teller, who considered an equivalent model in 1943. The Potts model is related to, and generalized by, several other models, including the XY model, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cellular Automaton
A cellular automaton (pl. cellular automata, abbrev. CA) is a discrete model of computation studied in automata theory. Cellular automata are also called cellular spaces, tessellation automata, homogeneous structures, cellular structures, tessellation structures, and iterative arrays. Cellular automata have found application in various areas, including physics, theoretical biology and microstructure modeling. A cellular automaton consists of a regular grid of ''cells'', each in one of a finite number of ''State (computer science), states'', such as ''on'' and ''off'' (in contrast to a coupled map lattice). The grid can be in any finite number of dimensions. For each cell, a set of cells called its ''neighborhood'' is defined relative to the specified cell. An initial state (time ''t'' = 0) is selected by assigning a state for each cell. A new ''generation'' is created (advancing ''t'' by 1), according to some fixed ''rule'' (generally, a mathematical function) that dete ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Computational Science
Computational science, also known as scientific computing, technical computing or scientific computation (SC), is a division of science, and more specifically the Computer Sciences, which uses advanced computing capabilities to understand and solve complex physical problems. While this typically extends into computational specializations, this field of study includes: * Algorithms ( numerical and non-numerical): mathematical models, computational models, and computer simulations developed to solve sciences (e.g, physical, biological, and social), engineering, and humanities problems * Computer hardware that develops and optimizes the advanced system hardware, firmware, networking, and data management components needed to solve computationally demanding problems * The computing infrastructure that supports both the science and engineering problem solving and the developmental computer and information science In practical use, it is typically the application of compu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Molecular Dynamics
Molecular dynamics (MD) is a computer simulation method for analyzing the Motion (physics), physical movements of atoms and molecules. The atoms and molecules are allowed to interact for a fixed period of time, giving a view of the dynamics (mechanics), dynamic "evolution" of the system. In the most common version, the trajectory, trajectories of atoms and molecules are determined by Numerical integration, numerically solving Newton's laws of motion, Newton's equations of motion for a system of interacting particles, where Force (physics), forces between the particles and their potential energy, potential energies are often calculated using interatomic potentials or molecular mechanics, molecular mechanical Force field (chemistry), force fields. The method is applied mostly in chemical physics, materials science, and biophysics. Because molecular systems typically consist of a vast number of particles, it is impossible to determine the properties of such complex systems analyt ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coarse-grained Modeling
Coarse-grained modeling, coarse-grained models, aim at simulating the behaviour of complex systems using their coarse-grained (simplified) representation. Coarse-grained models are widely used for molecular modeling of biomolecules at various granularity levels. A wide range of coarse-grained models have been proposed. They are usually dedicated to computational modeling of specific molecules: proteins, nucleic acids, lipid membranes, carbohydrates or water. In these models, molecules are represented not by individual atoms, but by "pseudo-atoms" approximating groups of atoms, such as whole amino acid residue. By decreasing the degrees of freedom much longer simulation times can be studied at the expense of molecular detail. Coarse-grained models have found practical applications in molecular dynamics simulations. Another case of interest is the simplification of a given discrete-state system, as very often descriptions of the same system at different levels of detail are possibl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Embedded Atom Model
In computational chemistry and computational physics, the embedded atom model, embedded-atom method or EAM, is an approximation describing the energy between atoms and is a type of interatomic potential. The energy is a function of a sum of functions of the separation between an atom and its neighbors. In the original model, by Murray Daw and Mike Baskes, the latter functions represent the electron density. The EAM is related to the second moment approximation to tight binding theory, also known as the Finnis-Sinclair model. These models are particularly appropriate for metallic systems. Embedded-atom methods are widely used in molecular dynamics simulations. Model simulation In a simulation, the potential energy of an atom, i, is given by :E_i = F_\alpha\left(\sum_ \rho_\beta (r_) \right) + \frac \sum_ \phi_(r_), where r_ is the distance between atoms i and j, \phi_ is a pair-wise potential function, \rho_\beta is the contribution to the electron charge density from atom j of typ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Covalent Bond
A covalent bond is a chemical bond that involves the sharing of electrons to form electron pairs between atoms. These electron pairs are known as shared pairs or bonding pairs. The stable balance of attractive and repulsive forces between atoms, when they share electrons, is known as covalent bonding. For many molecules, the sharing of electrons allows each atom to attain the equivalent of a full valence shell, corresponding to a stable electronic configuration. In organic chemistry, covalent bonding is much more common than ionic bonding. Covalent bonding also includes many kinds of interactions, including σ-bonding, π-bonding, metal-to-metal bonding, agostic interactions, bent bonds, three-center two-electron bonds and three-center four-electron bonds. The term "covalence" was introduced by Irving Langmuir in 1919, with Nevil Sidgwick using "co-valent link" in the 1920s. Merriam-Webster dates the specific phrase ''covalent bond'' to 1939, recognizing its first known use. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ionic Potential
Ionic potential is the ratio of the electrical charge (''z'') to the radius (''r'') of an ion. \text = \frac = \frac As such, this ratio is a measure of the charge density at the surface of the ion; usually the denser the charge, the stronger the bond formed by the ion with ions of opposite charge. The ionic potential gives an indication of how strongly, or weakly, the ion will be electrostatically attracted by ions of opposite charge; and to what extent the ion will be repelled by ions of the same charge. Victor Moritz Goldschmidt, the father of modern geochemistry found that the behavior of an element in its environment could be predicted from its ionic potential and illustrated this with a diagram (plot of the bare ionic radius as a function of the ionic charge). For instance, the solubility of dissolved iron is highly dependent on its redox state. with a lower ionic potential than is much more soluble because it exerts a weaker interaction force with ion present in wa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |