|
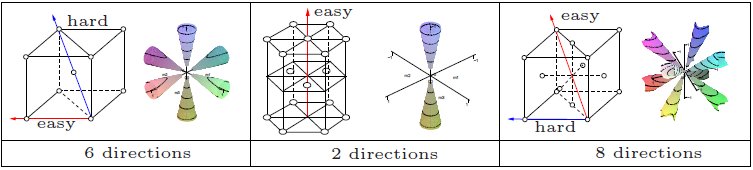
Magnetocrystalline Anisotropy
In physics, a ferromagnetic material is said to have magnetocrystalline anisotropy if it takes more energy to magnetization, magnetize it in certain directions than in others. These directions are usually related to the crystal structure, principal axes of its crystal lattice. It is a special case of magnetic anisotropy. In other words, the excess energy required to magnetize a specimen in a particular direction over that required to magnetize it along the easy direction is called crystalline anisotropy energy. Causes The spin-orbit interaction is the primary source of magnetocrystalline anisotropy. It is basically the orbital motion of the electrons which couples with crystal electric field giving rise to the first order contribution to magnetocrystalline anisotropy. The second order arises due to the mutual interaction of the magnetic dipoles. This effect is weak compared to the exchange interaction and is difficult to compute from first principles, although some successful co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Physics
Physics is the scientific study of matter, its Elementary particle, fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge which relates to the order of nature, or, in other words, to the regular succession of events." It is one of the most fundamental scientific disciplines. "Physics is one of the most fundamental of the sciences. Scientists of all disciplines use the ideas of physics, including chemists who study the structure of molecules, paleontologists who try to reconstruct how dinosaurs walked, and climatologists who study how human activities affect the atmosphere and oceans. Physics is also the foundation of all engineering and technology. No engineer could design a flat-screen TV, an interplanetary spacecraft, or even a better mousetrap without first understanding the basic laws of physics. (...) You will come to see physics as a towering achievement of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Direction Cosines
In analytic geometry, the direction cosines (or directional cosines) of a vector are the cosines of the angles between the vector and the three positive coordinate axes. Equivalently, they are the contributions of each component of the basis to a unit vector in that direction. Three-dimensional Cartesian coordinates If is a Euclidean vector in three-dimensional Euclidean space, \mathbf v = v_x \mathbf e_x + v_y \mathbf e_y + v_z \mathbf e_z, where are the standard basis in Cartesian notation, then the direction cosines are \begin \alpha &= \cos a = \frac &&= \frac,\\ \beta &= \cos b = \frac &&= \frac,\\ \gamma &= \cos c = \frac &&= \frac. \end It follows that by squaring each equation and adding the results \cos^2 a + \cos^2 b + \cos^2 c = \alpha^ + \beta^ + \gamma^ = 1. Here are the direction cosines and the Cartesian coordinates of the unit vector \tfrac, and are the direction angles of the vector . The direction angles are acute or obtuse angles, i.e. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tetragonal Crystal System
In crystallography, the tetragonal crystal system is one of the 7 crystal systems. Tetragonal crystal lattices result from stretching a cubic lattice along one of its lattice vectors, so that the cube becomes a rectangular prism with a square base (''a'' by ''a'') and height (''c'', which is different from ''a''). Bravais lattices There are two tetragonal Bravais lattices: the primitive tetragonal and the body-centered tetragonal. The body-centered tetragonal lattice is equivalent to the primitive tetragonal lattice with a smaller unit cell, while the face-centered tetragonal lattice is equivalent to the body-centered tetragonal lattice with a smaller unit cell. Crystal classes The point groups that fall under this crystal system are listed below, followed by their representations in international notation, Schoenflies notation, orbifold notation, Coxeter notation and mineral examples.Hurlbut, Cornelius S.; Klein, Cornelis, 1985, ''Manual of Mineralogy'', 20th ed ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Basal Plane
In crystallography, crystal structure is a description of ordered arrangement of atoms, ions, or molecules in a crystalline material. Ordered structures occur from intrinsic nature of constituent particles to form symmetric patterns that repeat along the principal directions of three-dimensional space in matter. The smallest group of particles in a material that constitutes this repeating pattern is the unit cell of the structure. The unit cell completely reflects the symmetry and structure of the entire crystal, which is built up by repetitive translation of the unit cell along its principal axes. The translation vectors define the nodes of the Bravais lattice. The lengths of principal axes/edges, of the unit cell and angles between them are lattice constants, also called ''lattice parameters'' or ''cell parameters''. The symmetry properties of a crystal are described by the concept of space groups. All possible symmetric arrangements of particles in three-dimensional space may ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Minima
In mathematical analysis, the maximum and minimum of a function are, respectively, the greatest and least value taken by the function. Known generically as extremum, they may be defined either within a given range (the ''local'' or ''relative'' extrema) or on the entire domain (the ''global'' or ''absolute'' extrema) of a function. Pierre de Fermat was one of the first mathematicians to propose a general technique, adequality, for finding the maxima and minima of functions. As defined in set theory, the maximum and minimum of a set are the greatest and least elements in the set, respectively. Unbounded infinite sets, such as the set of real numbers, have no minimum or maximum. In statistics, the corresponding concept is the sample maximum and minimum. Definition A real-valued function ''f'' defined on a domain ''X'' has a global (or absolute) maximum point at ''x''∗, if for all ''x'' in ''X''. Similarly, the function has a global (or absolute) minimum point at ''x''∗, if ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spherical Polar Coordinates
In mathematics, a spherical coordinate system specifies a given point in three-dimensional space by using a distance and two angles as its three coordinates. These are * the radial distance along the line connecting the point to a fixed point called the origin; * the polar angle between this radial line and a given ''polar axis''; and * the azimuthal angle , which is the angle of rotation of the radial line around the polar axis. (See graphic regarding the "physics convention".) Once the radius is fixed, the three coordinates (''r'', ''θ'', ''φ''), known as a 3-tuple, provide a coordinate system on a sphere, typically called the spherical polar coordinates. The plane passing through the origin and perpendicular to the polar axis (where the polar angle is a right angle) is called the ''reference plane'' (sometimes '' fundamental plane''). Terminology The radial distance from the fixed point of origin is also called the ''radius'', or ''radial line'', or ''radial coord ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Energy Density
In physics, energy density is the quotient between the amount of energy stored in a given system or contained in a given region of space and the volume of the system or region considered. Often only the ''useful'' or extractable energy is measured. It is sometimes confused with stored energy per unit mass, which is called ''specific energy'' or . There are different types of energy stored, corresponding to a particular type of reaction. In order of the typical magnitude of the energy stored, examples of reactions are: Nuclear power, nuclear, Chemical energy, chemical (including Electrochemistry, electrochemical), electrical, pressure, Deformation (engineering), material deformation or in Electromagnetic field, electromagnetic fields. Nuclear reactions take place in stars and nuclear power plants, both of which derive energy from the binding energy of nuclei. Chemical reactions are used by organisms to derive energy from food and by automobiles from the combustion of gasoline. Liqu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Uniaxial Anisotropy
In crystal optics, the index ellipsoid (also known as the optical indicatrix or sometimes as the dielectric ellipsoid) is a geometric construction which concisely represents the refractive indices and associated polarizations of light, as functions of the orientation of the wavefront, in a doubly-refractive crystal (provided that the crystal does not exhibit optical rotation). When this ellipsoid is cut through its center by a plane parallel to the wavefront, the resulting intersection (called a ''central section'' or ''diametral section'') is an ellipse whose major and minor semiaxes have lengths equal to the two refractive indices for that orientation of the wavefront, and have the directions of the respective polarizations as expressed by the electric displacement vector . The principal semiaxes of the index ellipsoid are called the ''principal refractive indices''. It follows from the sectioning procedure that each principal semiaxis of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Easy Axes
Easy is an adjective describing something that is not difficult to do. It may also refer to: Arts and entertainment Film and television * ''Easy'' (film), a 2003 American romantic comedy film *''Easy!'', or ''Scialla!'', a 2011 Italian comedy film * ''Easy'' (TV series), a 2016–2019 American comedy-drama anthology series Music Albums * ''Easy'' (Easybeats album), 1965 * ''Easy'' (Grant Green album), 1978 * ''Easy'' (Grinspoon album), 1999 * ''Easy'' (Kelly Willis album) or the title song, 2002 * ''Easy'' (Marvin Gaye and Tammi Terrell album), 1969 * ''Easy'' (Nancy Wilson album), 1968 * ''Easy'' (Ralph McTell album), 1974 *''Easy'', by Cowboy Mouth, 2000 EPs * ''Easy'' (EP), by Le Sserafim, 2024 Songs * "Easy" (Commodores song), 1977; covered by Faith No More, 1992 * "Easy" (Camila Cabello song), 2019 * "Easy" (Cro song), 2012 * "Easy" (DaniLeigh song), 2019 * "Easy" (Dragonette song), 2010 * "Easy" (Ice MC song), 1989 * "Easy" (KSI, Bugzy Malone and R3hab song), 2023 * "Eas ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Degree Of A Polynomial
In mathematics, the degree of a polynomial is the highest of the degrees of the polynomial's monomials (individual terms) with non-zero coefficients. The degree of a term is the sum of the exponents of the variables that appear in it, and thus is a non-negative integer. For a univariate polynomial, the degree of the polynomial is simply the highest exponent occurring in the polynomial. The term order has been used as a synonym of ''degree'' but, nowadays, may refer to several other concepts (see Order of a polynomial (other)). For example, the polynomial 7x^2y^3 + 4x - 9, which can also be written as 7x^2y^3 + 4x^1y^0 - 9x^0y^0, has three terms. The first term has a degree of 5 (the sum of the powers 2 and 3), the second term has a degree of 1, and the last term has a degree of 0. Therefore, the polynomial has a degree of 5, which is the highest degree of any term. To determine the degree of a polynomial that is not in standard form, such as (x+1)^2 - (x-1)^2, one c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hexagonal Crystal System
In crystallography, the hexagonal crystal family is one of the six crystal family, crystal families, which includes two crystal systems (hexagonal and trigonal) and two lattice systems (hexagonal and rhombohedral). While commonly confused, the trigonal crystal system and the rhombohedral lattice system are not equivalent (see section hexagonal crystal family#Crystal systems, crystal systems below). In particular, there are crystals that have trigonal symmetry but belong to the hexagonal lattice (such as α-quartz). The hexagonal crystal family consists of the 12 point groups such that at least one of their space groups has the hexagonal lattice as underlying lattice, and is the union of the hexagonal crystal system and the trigonal crystal system. There are 52 space groups associated with it, which are exactly those whose Bravais lattice is either hexagonal or rhombohedral. __TOC__ Lattice systems The hexagonal crystal family consists of two lattice systems: hexagonal and rhom ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cubic Crystal System
In crystallography, the cubic (or isometric) crystal system is a crystal system where the unit cell is in the shape of a cube. This is one of the most common and simplest shapes found in crystals and minerals. There are three main varieties of these crystals: *Primitive cubic (abbreviated ''cP'' and alternatively called simple cubic) *Body-centered cubic (abbreviated ''cI'' or bcc) *Face-centered cubic (abbreviated ''cF'' or fcc) Note: the term fcc is often used in synonym for the ''cubic close-packed'' or ccp structure occurring in metals. However, fcc stands for a face-centered cubic Bravais lattice, which is not necessarily close-packed when a motif is set onto the lattice points. E.g. the diamond and the zincblende lattices are fcc but not close-packed. Each is subdivided into other variants listed below. Although the ''unit cells'' in these crystals are conventionally taken to be cubes, the primitive unit cells often are not. Bravais lattices The three Bravais latices ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |