|
Light Ray
In optics, a ray is an idealized geometrical model of light or other electromagnetic radiation, obtained by choosing a curve that is perpendicular to the ''wavefronts'' of the actual light, and that points in the direction of energy flow. Rays are used to model the propagation of light through an optical system, by dividing the real light field up into discrete rays that can be computationally propagated through the system by the techniques of '' ray tracing''. This allows even very complex optical systems to be analyzed mathematically or simulated by computer. Ray tracing uses approximate solutions to Maxwell's equations that are valid as long as the light waves propagate through and around objects whose dimensions are much greater than the light's wavelength. '' Ray optics'' or ''geometrical optics'' does not describe phenomena such as diffraction, which require wave optics theory. Some wave phenomena such as interference can be modeled in limited circumstances by adding ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Geometrical Optics
Geometrical optics, or ray optics, is a model of optics that describes light Wave propagation, propagation in terms of ''ray (optics), rays''. The ray in geometrical optics is an abstract object, abstraction useful for approximating the paths along which light propagates under certain circumstances. The simplifying assumptions of geometrical optics include that light rays: * propagate in straight-line paths as they travel in a Homogeneity (physics), homogeneous medium * bend, and in particular circumstances may split in two, at the Interface (matter), interface between two dissimilar optical medium, media * follow curved paths in a medium in which the refractive index changes * may be absorbed or reflected. Geometrical optics does not account for certain optical effects such as diffraction and Interference (wave propagation), interference, which are considered in physical optics. This simplification is useful in practice; it is an excellent approximation when the wavelength is smal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Ray Optics
Geometrical optics, or ray optics, is a model of optics that describes light propagation in terms of '' rays''. The ray in geometrical optics is an abstraction useful for approximating the paths along which light propagates under certain circumstances. The simplifying assumptions of geometrical optics include that light rays: * propagate in straight-line paths as they travel in a homogeneous medium * bend, and in particular circumstances may split in two, at the interface between two dissimilar media * follow curved paths in a medium in which the refractive index changes * may be absorbed or reflected. Geometrical optics does not account for certain optical effects such as diffraction and interference, which are considered in physical optics. This simplification is useful in practice; it is an excellent approximation when the wavelength is small compared to the size of structures with which the light interacts. The techniques are particularly useful in describing geometrical aspect ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Hamiltonian Optics-Rays And Wavefronts
Hamiltonian may refer to: * Hamiltonian mechanics, a function that represents the total energy of a system * Hamiltonian (quantum mechanics), an operator corresponding to the total energy of that system ** Dyall Hamiltonian, a modified Hamiltonian with two-electron nature ** Molecular Hamiltonian, the Hamiltonian operator representing the energy of the electrons and nuclei in a molecule * Hamiltonian (control theory), a function used to solve a problem of optimal control for a dynamical system * Hamiltonian path, a path in a graph that visits each vertex exactly once * Hamiltonian matrix, a matrix with certain special properties commonly used in linear algebra * Hamiltonian group, a non-abelian group the subgroups of which are all normal * Hamiltonian economic program, the economic policies advocated by Alexander Hamilton, the first United States Secretary of the Treasury See also * Alexander Hamilton (1755 or 1757–1804), American statesman and one of the Founding Fathers of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
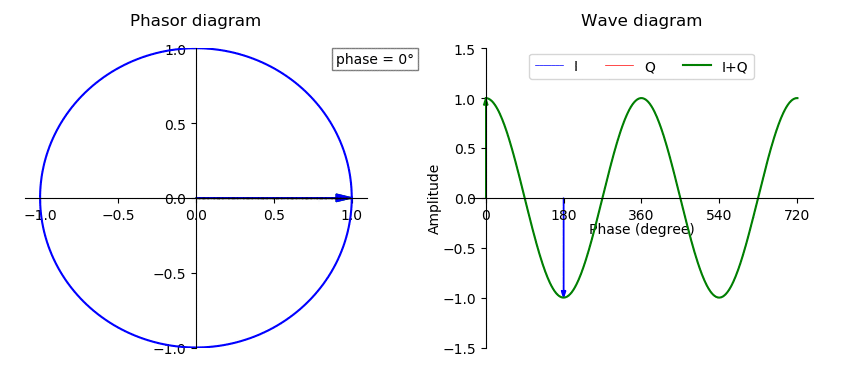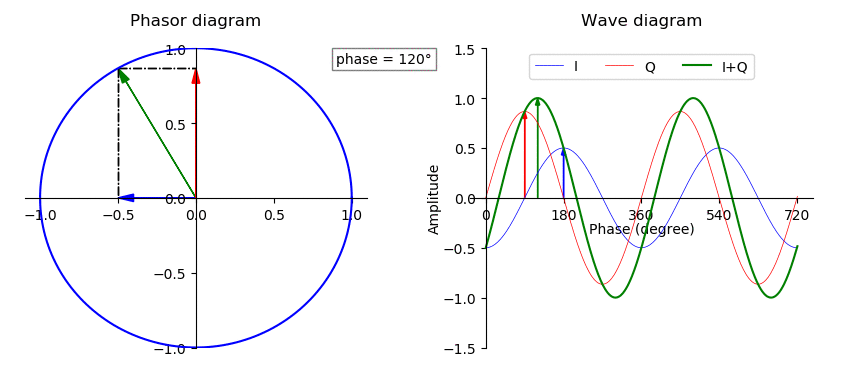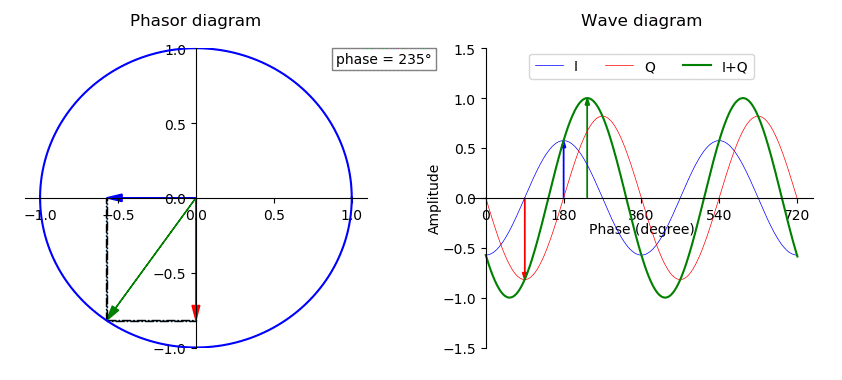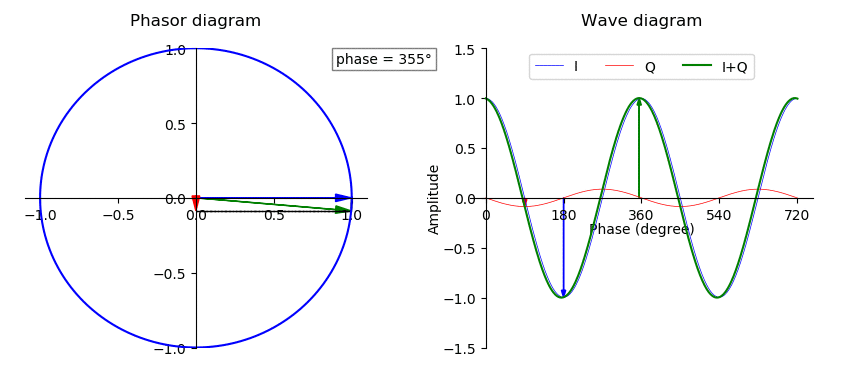 |
Phase (waves)
In physics and mathematics, the phase (symbol φ or ϕ) of a wave or other periodic function F of some real variable t (such as time) is an angle-like quantity representing the fraction of the cycle covered up to t. It is expressed in such a scale that it varies by one full turn as the variable t goes through each period (and F(t) goes through each complete cycle). It may be measured in any angular unit such as degrees or radians, thus increasing by 360° or 2\pi as the variable t completes a full period. This convention is especially appropriate for a sinusoidal function, since its value at any argument t then can be expressed as \varphi(t), the sine of the phase, multiplied by some factor (the amplitude of the sinusoid). (The cosine may be used instead of sine, depending on where one considers each period to start.) Usually, whole turns are ignored when expressing the phase; so that \varphi(t) is also a periodic function, with the same period as F, that repeatedly ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Fermat's Principle
Fermat's principle, also known as the principle of least time, is the link between geometrical optics, ray optics and physical optics, wave optics. Fermat's principle states that the path taken by a Ray (optics), ray between two given points is the path that can be traveled in the least time. First proposed by the French mathematician Pierre de Fermat in 1662, as a means of explaining the Snell's law, ordinary law of refraction of light (Fig.1), Fermat's principle was initially controversial because it seemed to ascribe knowledge and intent to nature. Not until the 19th century was it understood that nature's ability to test alternative paths is merely a fundamental property of waves. If points ''A'' and ''B'' are given, a wavefront expanding from ''A'' sweeps all possible ray paths radiating from ''A'', whether they pass through ''B'' or not. If the wavefront reaches point ''B'', it sweeps not only the ''ray'' path(s) from ''A'' to ''B'', but also an infinitude of near ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Geometric Optics
Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician who works in the field of geometry is called a '' geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point, line, plane, distance, angle, surface, and curve, as fundamental concepts. Originally developed to model the physical world, geometry has applications in almost all sciences, and also in art, architecture, and other activities that are related to graphics. Geometry also has applications in areas of mathematics that are apparently unrelated. For example, methods of algebraic geometry are fundamental in Wiles's proof of Fermat's Last Theorem, a problem that was stated in terms of elementary arithmetic, and remained unsolved for several centuries. Duri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
 |
Refractive Index
In optics, the refractive index (or refraction index) of an optical medium is the ratio of the apparent speed of light in the air or vacuum to the speed in the medium. The refractive index determines how much the path of light is bent, or refraction, refracted, when entering a material. This is described by Snell's law of refraction, , where and are the angle of incidence (optics), angle of incidence and angle of refraction, respectively, of a ray crossing the interface between two media with refractive indices and . The refractive indices also determine the amount of light that is reflectivity, reflected when reaching the interface, as well as the critical angle for total internal reflection, their intensity (Fresnel equations) and Brewster's angle. The refractive index, n, can be seen as the factor by which the speed and the wavelength of the radiation are reduced with respect to their vacuum values: the speed of light in a medium is , and similarly the wavelength in that me ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Optical Medium
In optics, an optical medium is material through which light and other electromagnetic waves propagate. It is a form of transmission medium. The permittivity and permeability of the medium define how electromagnetic waves propagate in it. Properties The optical medium has an '' intrinsic impedance'', given by ::\eta = where E_x and H_y are the electric field and magnetic field, respectively. In a region with no electrical conductivity, the expression simplifies to: ::\eta = \sqrt\ . For example, in free space the intrinsic impedance is called the characteristic impedance of vacuum, denoted ''Z''0, and ::Z_0 = \sqrt\ . Waves propagate through a medium with velocity c_w = \nu \lambda , where \nu is the frequency and \lambda is the wavelength of the electromagnetic waves. This equation also may be put in the form : c_w = \ , where \omega is the angular frequency of the wave and k is the wavenumber of the wave. In electrical engineering, the symbol \beta, called the '' phase ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Interface
Interface or interfacing may refer to: Academic journals * ''Interface'' (journal), by the Electrochemical Society * '' Interface, Journal of Applied Linguistics'', now merged with ''ITL International Journal of Applied Linguistics'' * '' Interface: A Journal for and About Social Movements'' * ''Interface'', shortened name for the ''Journal of the Royal Society Interface'', covering the interface between life sciences and physical sciences * ''Interfaces'' (journal), now ''INFORMS Journal on Applied Analytics'' Arts and entertainment * ''Interface'' (album), by Dominion, 1996 * Interface (band), an American music group * ''Interface'' (film), a 1984 American film * ''Interface'' (novel), by Stephen Bury (a pseudonym), 1994 * "Interface" (''Star Trek: The Next Generation''), an episode of the TV series * '' Interface series'', a science fiction horror story in short installments on Reddit Science and technology * Interface (computing), a shared boundary between system comp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Homogeneous Medium
In physics, a homogeneous material or system has the same properties at every point; it is uniform without irregularities. (accessed November 16, 2009). Tanton, James. "homogeneous." Encyclopedia of Mathematics. New York: Facts On File, Inc., 2005. Science Online. Facts On File, Inc. "A polynomial in several variables p(x,y,z,…) is called homogeneous ..more generally, a function of several variables f(x,y,z,…) is homogeneous ..Identifying homogeneous functions can be helpful in solving differential equations ndany formula that represents the mean of a set of numbers is required to be homogeneous. In physics, the term homogeneous describes a substance or an object whose properties do not vary with position. For example, an object of uniform density is sometimes described as homogeneous." James. homogeneous (math). (accessed: 2009-11-16) A uniform electric field (which has the same strength and the same direction at each point) would be compatible with homogeneity (all poi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Wave Vector
In physics, a wave vector (or wavevector) is a vector used in describing a wave, with a typical unit being cycle per metre. It has a magnitude and direction. Its magnitude is the wavenumber of the wave (inversely proportional to the wavelength), and its direction is perpendicular to the wavefront. In isotropic media, this is also the direction of wave propagation. A closely related vector is the angular wave vector (or angular wavevector), with a typical unit being radian per metre. The wave vector and angular wave vector are related by a fixed constant of proportionality, 2 radians per cycle. It is common in several fields of physics to refer to the angular wave vector simply as the ''wave vector'', in contrast to, for example, crystallography. It is also common to use the symbol for whichever is in use. In the context of special relativity, a '' wave four-vector'' can be defined, combining the (angular) wave vector and (angular) frequency. Definition The terms ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Collinear
In geometry, collinearity of a set of Point (geometry), points is the property of their lying on a single Line (geometry), line. A set of points with this property is said to be collinear (sometimes spelled as colinear). In greater generality, the term has been used for aligned objects, that is, things being "in a line" or "in a row". Points on a line In any geometry, the set of points on a line are said to be collinear. In Euclidean geometry this relation is intuitively visualized by points lying in a row on a "straight line". However, in most geometries (including Euclidean) a Line (geometry), line is typically a Primitive notion, primitive (undefined) object type, so such visualizations will not necessarily be appropriate. A Mathematical model, model for the geometry offers an interpretation of how the points, lines and other object types relate to one another and a notion such as collinearity must be interpreted within the context of that model. For instance, in spherical g ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |