|
Inverse Pythagorean Theorem
In geometry, the inverse Pythagorean theorem (also known as the reciprocal Pythagorean theorem or the upside down Pythagorean theorem) is as follows: :Let , be the endpoints of the hypotenuse of a right triangle . Let be the foot of a perpendicular dropped from , the vertex of the right angle, to the hypotenuse. Then :: \frac 1 = \frac 1 + \frac 1 . This theorem should not be confused with proposition 48 in book 1 of Euclid's '' Elements'', the converse of the Pythagorean theorem, which states that if the square on one side of a triangle is equal to the sum of the squares on the other two sides then the other two sides contain a right angle. Proof The area of triangle can be expressed in terms of either and , or and : :\begin \tfrac AC \cdot BC &= \tfrac AB \cdot CD \\ pt (AC \cdot BC)^2 &= (AB \cdot CD)^2 \\ pt \frac &= \frac \end given , and . Using the Pythagorean theorem, :\begin \frac &= \frac \\ pt &= \frac + \frac \\ pt\quad \the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometry
Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician who works in the field of geometry is called a ''List of geometers, geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point (geometry), point, line (geometry), line, plane (geometry), plane, distance, angle, surface (mathematics), surface, and curve, as fundamental concepts. Originally developed to model the physical world, geometry has applications in almost all sciences, and also in art, architecture, and other activities that are related to graphics. Geometry also has applications in areas of mathematics that are apparently unrelated. For example, methods of algebraic geometry are fundamental in Wiles's proof of Fermat's Last Theorem, Wiles's proof of Fermat's ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hypotenuse
In geometry, a hypotenuse is the side of a right triangle opposite to the right angle. It is the longest side of any such triangle; the two other shorter sides of such a triangle are called '' catheti'' or ''legs''. Every rectangle can be divided into a pair of right triangles by cutting it along either diagonal; the diagonals are the hypotenuses of these triangles. The length of the hypotenuse can be found using the Pythagorean theorem, which states that the square of the length of the hypotenuse equals the sum of the squares of the lengths of the two legs. Mathematically, this can be written as a^2 + b^2 = c^2, where ''a'' is the length of one leg, ''b'' is the length of another leg, and ''c'' is the length of the hypotenuse. For example, if one of the legs of a right angle has a length of 3 and the other has a length of 4, then their squares add up to 25 = 9 + 16 = 3 × 3 + 4 × 4. Since 25 is the square of the hypotenuse, the length of the hypotenuse is the square r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
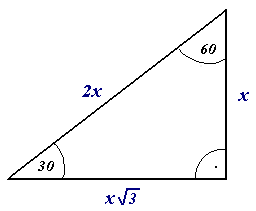
Right Triangle
A right triangle or right-angled triangle, sometimes called an orthogonal triangle or rectangular triangle, is a triangle in which two sides are perpendicular, forming a right angle ( turn or 90 degrees). The side opposite to the right angle is called the '' hypotenuse'' (side c in the figure). The sides adjacent to the right angle are called ''legs'' (or ''catheti'', singular: '' cathetus''). Side a may be identified as the side ''adjacent'' to angle B and ''opposite'' (or ''opposed to'') angle A, while side b is the side adjacent to angle A and opposite angle B. Every right triangle is half of a rectangle which has been divided along its diagonal. When the rectangle is a square, its right-triangular half is isosceles, with two congruent sides and two congruent angles. When the rectangle is not a square, its right-triangular half is scalene. Every triangle whose base is the diameter of a circle and whose apex lies on the circle is a right triangle, with the right angle at ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Altitude (triangle)
In geometry, an altitude of a triangle is a line segment through a given Vertex (geometry), vertex (called ''apex (geometry), apex'') and perpendicular to a line (geometry), line containing the side or edge (geometry), edge opposite the apex. This (finite) edge and (infinite) line extension are called, respectively, the ''base (geometry), base'' and ''extended side, extended base'' of the altitude. The point (geometry), point at the intersection of the extended base and the altitude is called the ''foot'' of the altitude. The length of the altitude, often simply called "the altitude" or "height", symbol , is the distance between the foot and the apex. The process of drawing the altitude from a vertex to the foot is known as ''dropping the altitude'' at that vertex. It is a special case of orthogonal projection. Altitudes can be used in the computation of the area of a triangle: one-half of the product of an altitude's length and its base's length (symbol ) equals the triangle's ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Right Angle
In geometry and trigonometry, a right angle is an angle of exactly 90 Degree (angle), degrees or radians corresponding to a quarter turn (geometry), turn. If a Line (mathematics)#Ray, ray is placed so that its endpoint is on a line and the adjacent angles are equal, then they are right angles. The term is a calque of Latin ''angulus rectus''; here ''rectus'' means "upright", referring to the vertical perpendicular to a horizontal base line. Closely related and important geometrical concepts are perpendicular lines, meaning lines that form right angles at their point of intersection, and orthogonality, which is the property of forming right angles, usually applied to Euclidean vector, vectors. The presence of a right angle in a triangle is the defining factor for right triangles, making the right angle basic to trigonometry. Etymology The meaning of ''right'' in ''right angle'' possibly refers to the Classical Latin, Latin adjective ''rectus'' 'erect, straight, upright, perp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclid
Euclid (; ; BC) was an ancient Greek mathematician active as a geometer and logician. Considered the "father of geometry", he is chiefly known for the '' Elements'' treatise, which established the foundations of geometry that largely dominated the field until the early 19th century. His system, now referred to as Euclidean geometry, involved innovations in combination with a synthesis of theories from earlier Greek mathematicians, including Eudoxus of Cnidus, Hippocrates of Chios, Thales and Theaetetus. With Archimedes and Apollonius of Perga, Euclid is generally considered among the greatest mathematicians of antiquity, and one of the most influential in the history of mathematics. Very little is known of Euclid's life, and most information comes from the scholars Proclus and Pappus of Alexandria many centuries later. Medieval Islamic mathematicians invented a fanciful biography, and medieval Byzantine and early Renaissance scholars mistook him for the earlier philo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclid's Elements
The ''Elements'' ( ) is a mathematics, mathematical treatise written 300 BC by the Ancient Greek mathematics, Ancient Greek mathematician Euclid. ''Elements'' is the oldest extant large-scale deductive treatment of mathematics. Drawing on the works of earlier mathematicians such as Hippocrates of Chios, Eudoxus of Cnidus and Theaetetus (mathematician), Theaetetus, the ''Elements'' is a collection in 13 books of definitions, postulates, propositions and mathematical proofs that covers plane and solid Euclidean geometry, elementary number theory, and Commensurability (mathematics), incommensurable lines. These include Pythagorean theorem, Thales' theorem, the Euclidean algorithm for greatest common divisors, Euclid's theorem that there are infinitely many prime numbers, and the Compass-and-straightedge construction, construction of regular polygons and Regular polyhedra, polyhedra. Often referred to as the most successful textbook ever written, the ''Elements'' has continued to be ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pythagorean Theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse (the side opposite the right angle) is equal to the sum of the areas of the squares on the other two sides. The theorem can be written as an equation relating the lengths of the sides , and the hypotenuse , sometimes called the Pythagorean equation: :a^2 + b^2 = c^2 . The theorem is named for the Ancient Greece, Greek philosopher Pythagoras, born around 570 BC. The theorem has been Mathematical proof, proved numerous times by many different methods – possibly the most for any mathematical theorem. The proofs are diverse, including both Geometry, geometric proofs and Algebra, algebraic proofs, with some dating back thousands of years. When Euclidean space is represented by a Cartesian coordinate system in analytic geometry, Euclidean distance satisfies th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cruciform Curve
In algebraic geometry, a quartic plane curve is a plane algebraic curve of the fourth degree. It can be defined by a bivariate quartic equation: :Ax^4+By^4+Cx^3y+Dx^2y^2+Exy^3+Fx^3+Gy^3+Hx^2y+Ixy^2+Jx^2+Ky^2+Lxy+Mx+Ny+P=0, with at least one of not equal to zero. This equation has 15 constants. However, it can be multiplied by any non-zero constant without changing the curve; thus by the choice of an appropriate constant of multiplication, any one of the coefficients can be set to 1, leaving only 14 constants. Therefore, the space of quartic curves can be identified with the real projective space It also follows, from Cramer's theorem on algebraic curves, that there is exactly one quartic curve that passes through a set of 14 distinct points in general position, since a quartic has 14 degrees of freedom. A quartic curve can have a maximum of: * Four connected components * Twenty-eight bi-tangents * Three ordinary double points. One may also consider quartic curves over oth ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parameter
A parameter (), generally, is any characteristic that can help in defining or classifying a particular system (meaning an event, project, object, situation, etc.). That is, a parameter is an element of a system that is useful, or critical, when identifying the system, or when evaluating its performance, status, condition, etc. ''Parameter'' has more specific meanings within various disciplines, including mathematics, computer programming, engineering, statistics, logic, linguistics, and electronic musical composition. In addition to its technical uses, there are also extended uses, especially in non-scientific contexts, where it is used to mean defining characteristics or boundaries, as in the phrases 'test parameters' or 'game play parameters'. Modelization When a system theory, system is modeled by equations, the values that describe the system are called ''parameters''. For example, in mechanics, the masses, the dimensions and shapes (for solid bodies), the densities and t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |