|
Interior Reconstruction
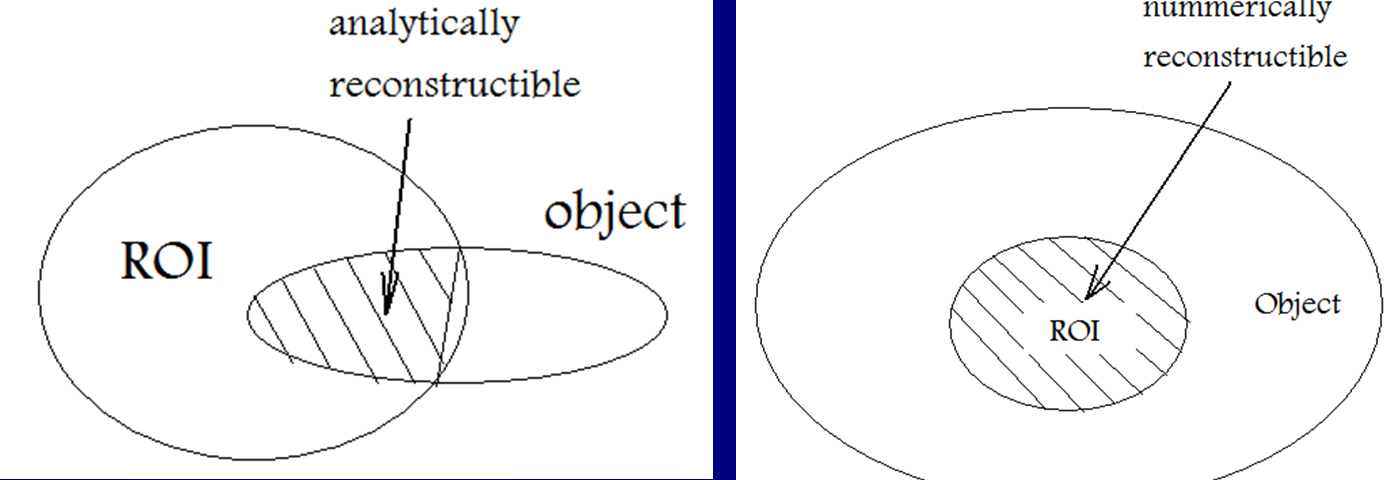
In iterative reconstruction in digital imaging, interior reconstruction (also known as limited field of view (LFV) reconstruction) is a technique to correct truncation artifacts caused by limiting image data to a small field of view. The reconstruction focuses on an area known as the region of interest (ROI). Although interior reconstruction can be applied to dental or cardiac X-ray computed tomography, CT images, the concept is not limited to CT. It is applied with one of several methods. Methods The purpose of each method is to solve for vector x in the following problem: : \begin f \\ g \end= \begin A & B \\ C & D \end \begin x \\ y \end. Let X be the region of interest (ROI) and Y be the region outside of X. Assume A, B, C, D are known matrices; x and y are unknown vectors of the original image, while f and g are vector measurements of the responses (f is known and g is unknown). x is inside region X, (x \in X) and y, in the region Y, (y \in Y), is outside region X. f is i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Iterative Reconstruction
Iterative reconstruction refers to Iteration, iterative algorithms used to reconstruct 2D and 3D reconstruction, 3D images in certain Digital imaging, imaging techniques. For example, in computed tomography an image must be reconstructed from projections of an object. Here, iterative reconstruction techniques are usually a better, but computationally more expensive alternative to the common filtered back projection (FBP) method, which directly calculates the image in a single reconstruction step.Herman, G. T.Fundamentals of computerized tomography: Image reconstruction from projection 2nd edition, Springer, 2009 In recent research works, scientists have shown that extremely fast computations and massive parallelism is possible for iterative reconstruction, which makes iterative reconstruction practical for commercialization. Basic concepts The reconstruction of an image from the acquired data is an inverse problem. Often, it is not possible to exactly solve the inverse problem ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Forecasting
Forecasting is the process of making predictions based on past and present data. Later these can be compared with what actually happens. For example, a company might Estimation, estimate their revenue in the next year, then compare it against the actual results creating a variance actual analysis. Prediction is a similar but more general term. Forecasting might refer to specific formal statistical methods employing time series, cross-sectional data, cross-sectional or longitudinal study, longitudinal data, or alternatively to less formal judgmental methods or the process of prediction and assessment of its accuracy. Usage can vary between areas of application: for example, in hydrology the terms "forecast" and "forecasting" are sometimes reserved for estimates of values at certain specific future times, while the term "prediction" is used for more general estimates, such as the number of times floods will occur over a long period. Risk and uncertainty are central to forecasting an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Generalized Inverse
In mathematics, and in particular, algebra, a generalized inverse (or, g-inverse) of an element ''x'' is an element ''y'' that has some properties of an inverse element but not necessarily all of them. The purpose of constructing a generalized inverse of a matrix is to obtain a matrix that can serve as an inverse in some sense for a wider class of matrices than invertible matrices. Generalized inverses can be defined in any mathematical structure that involves associative multiplication, that is, in a semigroup. This article describes generalized inverses of a matrix A. A matrix A^\mathrm \in \mathbb^ is a generalized inverse of a matrix A \in \mathbb^ if AA^\mathrmA = A. A generalized inverse exists for an arbitrary matrix, and when a matrix has a regular inverse, this inverse is its unique generalized inverse. Motivation Consider the linear system :Ax = y where A is an m \times n matrix and y \in \mathcal C(A), the column space of A. If m = n and A is nonsingula ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Local Inverse
In mathematics, the inverse function of a function (also called the inverse of ) is a function that undoes the operation of . The inverse of exists if and only if is bijective, and if it exists, is denoted by f^ . For a function f\colon X\to Y, its inverse f^\colon Y\to X admits an explicit description: it sends each element y\in Y to the unique element x\in X such that . As an example, consider the real-valued function of a real variable given by . One can think of as the function which multiplies its input by 5 then subtracts 7 from the result. To undo this, one adds 7 to the input, then divides the result by 5. Therefore, the inverse of is the function f^\colon \R\to\R defined by f^(y) = \frac . Definitions Let be a function whose domain is the set , and whose codomain is the set . Then is ''invertible'' if there exists a function from to such that g(f(x))=x for all x\in X and f(g(y))=y for all y\in Y. If is invertible, then there is exactly one function sat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Image Reconstruction
Iterative reconstruction refers to Iteration, iterative algorithms used to reconstruct 2D and 3D reconstruction, 3D images in certain Digital imaging, imaging techniques. For example, in computed tomography an image must be reconstructed from projections of an object. Here, iterative reconstruction techniques are usually a better, but computationally more expensive alternative to the common filtered back projection (FBP) method, which directly calculates the image in a single reconstruction step.Herman, G. T.Fundamentals of computerized tomography: Image reconstruction from projection 2nd edition, Springer, 2009 In recent research works, scientists have shown that extremely fast computations and massive parallelism is possible for iterative reconstruction, which makes iterative reconstruction practical for commercialization. Basic concepts The reconstruction of an image from the acquired data is an inverse problem. Often, it is not possible to exactly solve the inverse problem ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dead Reckoning
In navigation, dead reckoning is the process of calculating the current position of a moving object by using a previously determined position, or fix, and incorporating estimates of speed, heading (or direction or course), and elapsed time. The corresponding term in biology, to describe the processes by which animals update their estimates of position or heading, is path integration. Advances in navigational aids that give accurate information on position, in particular satellite navigation using the Global Positioning System, have made simple dead reckoning by humans obsolete for most purposes. However, inertial navigation systems, which provide very accurate directional information, use dead reckoning and are very widely applied. Etymology Contrary to myth, the term "dead reckoning" was not originally used to abbreviate "deduced reckoning", nor is it a misspelling of the term "ded reckoning". The use of "ded" or "deduced reckoning" is not known to have appeared earlier th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Extrapolation Domain Analysis
Extrapolation domain analysis (EDA) is a methodology for identifying geographical areas that seem suitable for adoption of innovative ecosystem management practices on the basis of sites exhibiting similarity in conditions such as climatic, land use and socioeconomic indicators. Whilst it has been applied to water research projects in nine pilot basins, the concept is generic and can be applied to any project where accelerating change being considered as a central development objective. The outputs of the method thus far have been used to quantify the global economic impact of implementing particular innovations together with its effect on water resources. The research has stimulated members of several of the Challenge Program for Water and Food projects to explore potential areas for scaling out. Such is the case of the Quesungual agroforestry system in Honduras, which is moving towards new areas in parallel with areas identified by the EDA method. EDA is a combined approach that ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Interpolation
In the mathematics, mathematical field of numerical analysis, interpolation is a type of estimation, a method of constructing (finding) new data points based on the range of a discrete set of known data points. In engineering and science, one often has a number of data points, obtained by sampling (statistics), sampling or experimentation, which represent the values of a function for a limited number of values of the Dependent and independent variables, independent variable. It is often required to interpolate; that is, estimate the value of that function for an intermediate value of the independent variable. A closely related problem is the function approximation, approximation of a complicated function by a simple function. Suppose the formula for some given function is known, but too complicated to evaluate efficiently. A few data points from the original function can be interpolated to produce a simpler function which is still fairly close to the original. The resulting gai ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trend Estimation
Linear trend estimation is a statistical technique used to analyze data patterns. Data patterns, or trends, occur when the information gathered tends to increase or decrease over time or is influenced by changes in an external factor. Linear trend estimation essentially creates a straight line on a graph of data that models the general direction that the data is heading. Fitting a trend: Least-squares Given a set of data, there are a variety of functions that can be chosen to fit the data. The simplest function is a straight line with the dependent variable (typically the measured data) on the vertical axis and the independent variable (often time) on the horizontal axis. The least-squares fit is a common method to fit a straight line through the data. This method minimizes the sum of the squared errors in the data series y. Given a set of points in time t and data values y_t observed for those points in time, values of \hat a and \hat b are chosen to minimize the sum of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Static Analysis
Static analysis, static projection, or static scoring is a simplified analysis wherein the effect of an immediate change to a system is calculated without regard to the longer-term response of the system to that change. If the short-term effect is then extrapolated to the long term, such extrapolation is inappropriate. Its opposite, dynamic analysis or dynamic scoring, is an attempt to take into account how the system is likely to respond to the change over time. One common use of these terms is budget policy in the United States, although it also occurs in many other statistical disputes. Examples A famous example of extrapolation of static analysis comes from overpopulation theory. Starting with Thomas Malthus at the end of the 18th century, various commentators have projected some short-term population growth trend for years into the future, resulting in the prediction that there would be disastrous overpopulation within a generation or two. Malthus himself essentially cla ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Richardson Extrapolation
In numerical analysis, Richardson extrapolation is a Series acceleration, sequence acceleration method used to improve the rate of convergence of a sequence of estimates of some value A^\ast = \lim_ A(h). In essence, given the value of A(h) for several values of h, we can estimate A^\ast by extrapolating the estimates to h=0. It is named after Lewis Fry Richardson, who introduced the technique in the early 20th century, though the idea was already known to Christiaan Huygens in Christiaan_Huygens#De_Circuli_Magnitudine_Inventa, his calculation of \pi. In the words of Garrett Birkhoff, Birkhoff and Gian-Carlo Rota, Rota, "its usefulness for practical computations can hardly be overestimated."Page 126 of Practical applications of Richardson extrapolation include Romberg integration, which applies Richardson extrapolation to the trapezoid rule, and the Bulirsch–Stoer algorithm for solving ordinary differential equations. General formula Notation Let A_0(h) be an approximation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |