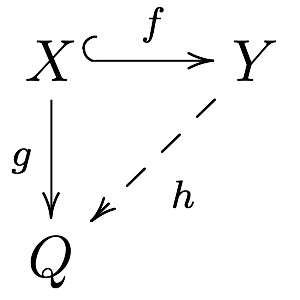|
Injective Metric Space
In metric geometry, an injective metric space, or equivalently a hyperconvex metric space, is a metric space with certain properties generalizing those of the real line and of L∞ distances in higher- dimensional vector spaces. These properties can be defined in two seemingly different ways: hyperconvexity involves the intersection properties of closed balls in the space, while injectivity involves the isometric embeddings of the space into larger spaces. However it is a theorem of that these two different types of definitions are equivalent. Hyperconvexity A metric space X is said to be hyperconvex if it is convex and its closed balls have the binary Helly property. That is: #Any two points x and y can be connected by the isometric image of a line segment of length equal to the distance between the points (i.e. X is a path space). #If F is any family of closed balls _r(p) = \ such that each pair of balls in F meets, then there exists a point x common to all the balls in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Metric Geometry
In mathematics, a metric space is a Set (mathematics), set together with a notion of ''distance'' between its Element (mathematics), elements, usually called point (geometry), points. The distance is measured by a function (mathematics), function called a metric or distance function. Metric spaces are a general setting for studying many of the concepts of mathematical analysis and geometry. The most familiar example of a metric space is 3-dimensional Euclidean space with its usual notion of distance. Other well-known examples are a sphere equipped with the angular distance and the hyperbolic plane. A metric may correspond to a Conceptual metaphor , metaphorical, rather than physical, notion of distance: for example, the set of 100-character Unicode strings can be equipped with the Hamming distance, which measures the number of characters that need to be changed to get from one string to another. Since they are very general, metric spaces are a tool used in many different bra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tight Span
In metric geometry, the metric envelope or tight span of a metric space ''M'' is an injective metric space into which ''M'' can be embedded. In some sense it consists of all points "between" the points of ''M'', analogous to the convex hull of a point set in a Euclidean space. The tight span is also sometimes known as the injective envelope or hyperconvex hull of ''M''. It has also been called the injective hull, but should not be confused with the injective hull of a module in algebra, a concept with a similar description relative to the category of ''R''-modules rather than metric spaces. The tight span was first described by , and it was studied and applied by Holsztyński in the 1960s. It was later independently rediscovered by and ; see for this history. The tight span is one of the central constructions of T-theory. Definition The tight span of a metric space can be defined as follows. Let (''X'',''d'') be a metric space, and let ''T''(''X'') be the set of extremal funct ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Category Of Metric Spaces
In category theory, Met is a category that has metric spaces as its objects and metric maps ( continuous functions between metric spaces that do not increase any pairwise distance) as its morphisms. This is a category because the composition of two metric maps is again a metric map. It was first considered by . Arrows The monomorphisms in Met are the injective metric maps. The epimorphisms are the metric maps for which the domain of the map has a dense image in the range. The isomorphisms are the isometries, i.e. metric maps which are injective, surjective, and distance-preserving. As an example, the inclusion of the rational numbers into the real numbers is a monomorphism and an epimorphism, but it is clearly not an isomorphism; this example shows that Met is not a balanced category. Objects The empty metric space is the initial object of Met; any singleton metric space is a terminal object. Because the initial object and the terminal objects differ, there are no zero objec ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Category (mathematics)
In mathematics, a category (sometimes called an abstract category to distinguish it from a concrete category) is a collection of "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose objects are sets and whose arrows are functions. ''Category theory'' is a branch of mathematics that seeks to generalize all of mathematics in terms of categories, independent of what their objects and arrows represent. Virtually every branch of modern mathematics can be described in terms of categories, and doing so often reveals deep insights and similarities between seemingly different areas of mathematics. As such, category theory provides an alternative foundation for mathematics to set theory and other proposed axiomatic foundations. In general, the objects and arrows may be abstract entities of any kind, and the n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Injective Object
In mathematics, especially in the field of category theory, the concept of injective object is a generalization of the concept of injective module. This concept is important in cohomology, in homotopy theory and in the theory of model categories. The dual notion is that of a projective object. Definition An object Q in a category \mathbf is said to be injective if for every monomorphism f: X \to Y and every morphism g: X \to Q there exists a morphism h: Y \to Q extending g to Y, i.e. such that h \circ f = g. That is, every morphism X \to Q factors through every monomorphism X \hookrightarrow Y. The morphism h in the above definition is not required to be uniquely determined by f and g. In a locally small category, it is equivalent to require that the hom functor \operatorname_(-,Q) carries monomorphisms in \mathbf to surjective set maps. In Abelian categories The notion of injectivity was first formulated for abelian categories, and this is still one of its primary areas of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
If And Only If
In logic and related fields such as mathematics and philosophy, "if and only if" (often shortened as "iff") is paraphrased by the biconditional, a logical connective between statements. The biconditional is true in two cases, where either both statements are true or both are false. The connective is biconditional (a statement of material equivalence), and can be likened to the standard material conditional ("only if", equal to "if ... then") combined with its reverse ("if"); hence the name. The result is that the truth of either one of the connected statements requires the truth of the other (i.e. either both statements are true, or both are false), though it is controversial whether the connective thus defined is properly rendered by the English "if and only if"—with its pre-existing meaning. For example, ''P if and only if Q'' means that ''P'' is true whenever ''Q'' is true, and the only case in which ''P'' is true is if ''Q'' is also true, whereas in the case of ''P if Q ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fixed-point Theorem
In mathematics, a fixed-point theorem is a result saying that a function ''F'' will have at least one fixed point (a point ''x'' for which ''F''(''x'') = ''x''), under some conditions on ''F'' that can be stated in general terms. In mathematical analysis The Banach fixed-point theorem (1922) gives a general criterion guaranteeing that, if it is satisfied, the procedure of iterating a function yields a fixed point. By contrast, the Brouwer fixed-point theorem (1911) is a non- constructive result: it says that any continuous function from the closed unit ball in ''n''-dimensional Euclidean space to itself must have a fixed point, but it doesn't describe how to find the fixed point (see also Sperner's lemma). For example, the cosine function is continuous in ��1, 1and maps it into ��1, 1 and thus must have a fixed point. This is clear when examining a sketched graph of the cosine function; the fixed point occurs where the cosine curve ''y'' = cos(''x'') intersect ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Short Map
In the mathematical theory of metric spaces, a metric map is a function between metric spaces that does not increase any distance. These maps are the morphisms in the category of metric spaces, Met. Such functions are always continuous functions. They are also called Lipschitz functions with Lipschitz constant 1, nonexpansive maps, nonexpanding maps, weak contractions, or short maps. Specifically, suppose that X and Y are metric spaces and f is a function from X to Y. Thus we have a metric map when, for any points x and y in X, d_(f(x),f(y)) \leq d_(x,y) . \! Here d_X and d_Y denote the metrics on X and Y respectively. Examples Consider the metric space ,1/2/math> with the Euclidean metric. Then the function f(x)=x^2 is a metric map, since for x\ne y, , f(x)-f(y), =, x+y, , x-y, <, x-y, . Category of metric maps The |
Complete Space
In mathematical analysis, a metric space is called complete (or a Cauchy space) if every Cauchy sequence of points in has a limit that is also in . Intuitively, a space is complete if there are no "points missing" from it (inside or at the boundary). For instance, the set of rational numbers is not complete, because e.g. \sqrt is "missing" from it, even though one can construct a Cauchy sequence of rational numbers that converges to it (see further examples below). It is always possible to "fill all the holes", leading to the ''completion'' of a given space, as explained below. Definition Cauchy sequence A sequence x_1, x_2, x_3, \ldots of elements from X of a metric space (X, d) is called Cauchy if for every positive real number r > 0 there is a positive integer N such that for all positive integers m, n > N, d(x_m, x_n) < r. Complete space A metric space is complete if any of the following equivalent conditions are satisfied: #Every Cauchy se ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jung's Theorem
In geometry, Jung's theorem is an inequality (mathematics), inequality between the diameter of a set of points in any Euclidean space and the radius of the circumradius, minimum enclosing ball of that set. It is named after Heinrich Jung, who first studied this inequality in 1901. Algorithms also exist to solve the smallest-circle problem explicitly. Statement Consider a compact set :K \subset \mathbb^n and let :d = \max_ \, p - q \, _2 be the diameter of ''K'', that is, the largest distance, Euclidean distance between any two of its points. Jung's theorem states that there exists a closed ball with radius :r \leq d \sqrt that contains ''K''. The boundary case of equality is attained by the regular ''n''-simplex. Jung's theorem in the plane The most common case of Jung's theorem is in the Euclidean plane, plane, that is, when ''n'' = 2. In this case the theorem states that there exists a circle enclosing all points whose radius satisfies :r \leq \frac, and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diameter
In geometry, a diameter of a circle is any straight line segment that passes through the centre of the circle and whose endpoints lie on the circle. It can also be defined as the longest Chord (geometry), chord of the circle. Both definitions are also valid for the diameter of a sphere. In more modern usage, the length d of a diameter is also called the diameter. In this sense one speaks of diameter rather than diameter (which refers to the line segment itself), because all diameters of a circle or sphere have the same length, this being twice the radius r. :d = 2r \qquad\text\qquad r = \frac. The word "diameter" is derived from (), "diameter of a circle", from (), "across, through" and (), "measure". It is often abbreviated \text, \text, d, or \varnothing. Constructions With straightedge and compass, a diameter of a given circle can be constructed as the perpendicular bisector of an arbitrary chord. Drawing two diameters in this way can be used to locate the center of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |