|
Information Projection
In information theory, the information projection or I-projection of a probability distribution ''q'' onto a set of distributions ''P'' is :p^* = \underset \operatorname_(p, , q). where D_ is the Kullback–Leibler divergence from ''q'' to ''p''. Viewing the Kullback–Leibler divergence as a measure of distance, the I-projection p^* is the "closest" distribution to ''q'' of all the distributions in ''P''. The I-projection is useful in setting up information geometry, notably because of the following inequality, valid when ''P'' is convex: \operatorname_(p, , q) \geq \operatorname_(p, , p^*) + \operatorname_(p^*, , q). This inequality can be interpreted as an information-geometric version of Pythagoras' triangle-inequality theorem, where KL divergence is viewed as squared distance in a Euclidean space. It is worthwhile to note that since \operatorname_(p, , q) \geq 0 and continuous in p, if ''P'' is closed and non-empty, then there exists at least one minimizer to the optimiz ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Information Theory
Information theory is the mathematical study of the quantification (science), quantification, Data storage, storage, and telecommunications, communication of information. The field was established and formalized by Claude Shannon in the 1940s, though early contributions were made in the 1920s through the works of Harry Nyquist and Ralph Hartley. It is at the intersection of electronic engineering, mathematics, statistics, computer science, Neuroscience, neurobiology, physics, and electrical engineering. A key measure in information theory is information entropy, entropy. Entropy quantifies the amount of uncertainty involved in the value of a random variable or the outcome of a random process. For example, identifying the outcome of a Fair coin, fair coin flip (which has two equally likely outcomes) provides less information (lower entropy, less uncertainty) than identifying the outcome from a roll of a dice, die (which has six equally likely outcomes). Some other important measu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability Distribution
In probability theory and statistics, a probability distribution is a Function (mathematics), function that gives the probabilities of occurrence of possible events for an Experiment (probability theory), experiment. It is a mathematical description of a Randomness, random phenomenon in terms of its sample space and the Probability, probabilities of Event (probability theory), events (subsets of the sample space). For instance, if is used to denote the outcome of a coin toss ("the experiment"), then the probability distribution of would take the value 0.5 (1 in 2 or 1/2) for , and 0.5 for (assuming that fair coin, the coin is fair). More commonly, probability distributions are used to compare the relative occurrence of many different random values. Probability distributions can be defined in different ways and for discrete or for continuous variables. Distributions with special properties or for especially important applications are given specific names. Introduction A prob ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
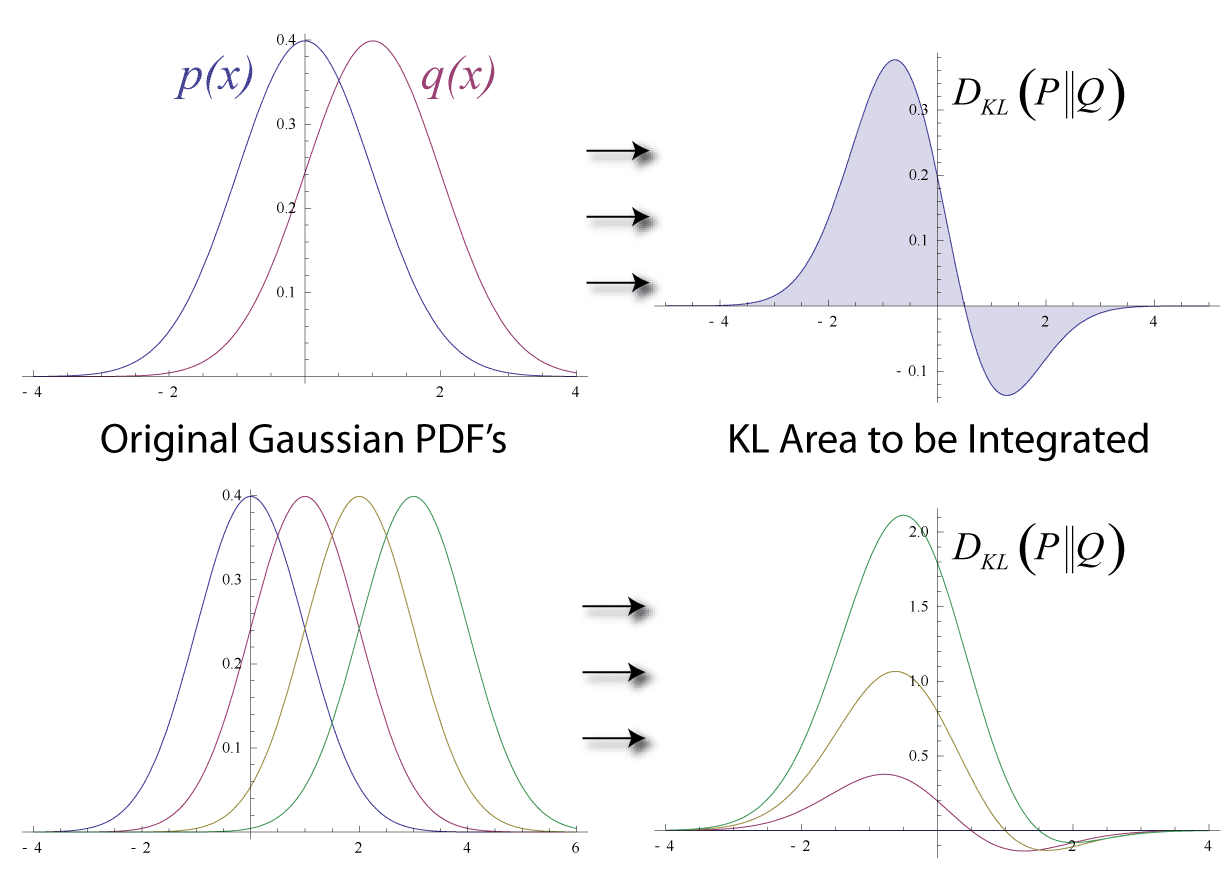
Kullback–Leibler Divergence
In mathematical statistics, the Kullback–Leibler (KL) divergence (also called relative entropy and I-divergence), denoted D_\text(P \parallel Q), is a type of statistical distance: a measure of how much a model probability distribution is different from a true probability distribution . Mathematically, it is defined as D_\text(P \parallel Q) = \sum_ P(x) \, \log \frac\text A simple interpretation of the KL divergence of from is the expected excess surprise from using as a model instead of when the actual distribution is . While it is a measure of how different two distributions are and is thus a distance in some sense, it is not actually a metric, which is the most familiar and formal type of distance. In particular, it is not symmetric in the two distributions (in contrast to variation of information), and does not satisfy the triangle inequality. Instead, in terms of information geometry, it is a type of divergence, a generalization of squared distance, and for cer ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Information Geometry
Information geometry is an interdisciplinary field that applies the techniques of differential geometry to study probability theory and statistics. It studies statistical manifolds, which are Riemannian manifolds whose points correspond to probability distributions. Introduction Historically, information geometry can be traced back to the work of C. R. Rao, who was the first to treat the Fisher matrix as a Riemannian metric. The modern theory is largely due to Shun'ichi Amari, whose work has been greatly influential on the development of the field. Classically, information geometry considered a parametrized statistical model as a Riemannian manifold, Riemannian, conjugate connection, statistical, and dually flat manifolds. Unlike usual smooth manifolds with tensor metric and Levi-Civita connection, these take into account conjugate connection, torsion, and Amari-Chentsov metric. All presented above geometric structures find application in information theory and machine lea ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
E-values
In statistical hypothesis testing, e-values quantify the evidence in the data against a null hypothesis (e.g., "the coin is fair", or, in a medical context, "this new treatment has no effect"). They serve as a more robust alternative to p-values, addressing some shortcomings of the latter. In contrast to p-values, e-values can deal with optional continuation: e-values of subsequent experiments (e.g. clinical trials concerning the same treatment) may simply be multiplied to provide a new, "product" e-value that represents the evidence in the joint experiment. This works even if, as often happens in practice, the decision to perform later experiments may depend in vague, unknown ways on the data observed in earlier experiments, and it is not known beforehand how many trials will be conducted: the product e-value remains a meaningful quantity, leading to tests with Type-I error control. For this reason, e-values and their sequential extension, the ''e-process'', are the fundamental ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
F-divergence
In probability theory, an f-divergence is a certain type of function D_f(P\, Q) that measures the difference between two probability distributions P and Q. Many common divergences, such as KL-divergence, Hellinger distance, and total variation distance, are special cases of f-divergence. History These divergences were introduced by Alfréd Rényi in the same paper where he introduced the well-known Rényi entropy. He proved that these divergences decrease in Markov Process, Markov processes. ''f''-divergences were studied further independently by , and and are sometimes known as Csiszár f-divergences, Csiszár–Morimoto divergences, or Ali–Silvey distances. Definition Non-singular case Let P and Q be two probability distributions over a space \Omega, such that P\ll Q, that is, P is Absolute continuity#Absolute continuity of measures, absolutely continuous with respect to Q (meaning Q>0 wherever P>0). Then, for a convex function f: [0, +\infty)\to(-\infty, +\infty] ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Divergence (statistics)
In information geometry, a divergence is a kind of statistical distance: a binary function which establishes the separation from one probability distribution to another on a statistical manifold. The simplest divergence is squared Euclidean distance (SED), and divergences can be viewed as generalizations of SED. The other most important divergence is relative entropy (also called Kullback–Leibler divergence), which is central to information theory. There are numerous other specific divergences and classes of divergences, notably ''f''-divergences and Bregman divergences (see ). Definition Given a differentiable manifold M of dimension n, a divergence on M is a C^2-function D: M\times M\to [0, \infty) satisfying: # D(p, q) \geq 0 for all p, q \in M (non-negativity), # D(p, q) = 0 if and only if p=q (positivity), # At every point p\in M, D(p, p+dp) is a positive-definite quadratic form for infinitesimal displacements dp from p. In applications to statistics, the manifold M i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sanov's Theorem
In mathematics and information theory, Sanov's theorem gives a bound on the probability of observing an atypical sequence of samples from a given probability distribution. In the language of large deviations theory, Sanov's theorem identifies the rate function for large deviations of the empirical measure of a sequence of i.i.d. random variables. Let ''A'' be a set of probability distributions over an alphabet ''X'', and let ''q'' be an arbitrary distribution over ''X'' (where ''q'' may or may not be in ''A''). Suppose we draw ''n'' i.i.d. samples from ''q'', represented by the vector x^n = (x_1, x_2, \ldots, x_n). Then, we have the following bound on the probability that the empirical measure \hat_ of the samples falls within the set ''A'': :q^n(\hat_\in A) \le (n+1)^ 2^, where * q^n is the joint probability distribution on X^n, and * p^* is the information projection of ''q'' onto ''A''. * D_(P \, Q), the KL divergence, is given by: D_(P \, Q) = \sum_ P(x) \log \frac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |