|
Imputation (statistics)
In statistics, imputation is the process of replacing missing data with substituted values. When substituting for a data point, it is known as "unit imputation"; when substituting for a component of a data point, it is known as "item imputation". There are three main problems that missing data causes: missing data can introduce a substantial amount of bias, make the handling and analysis of the data more arduous, and create reductions in efficiency. Because missing data can create problems for analyzing data, imputation is seen as a way to avoid pitfalls involved with listwise deletion of cases that have missing values. That is to say, when one or more values are missing for a case, most statistical packages default to discarding any case that has a missing value, which may introduce bias or affect the representativeness of the results. Imputation preserves all cases by replacing missing data with an estimated value based on other available information. Once all missing values ha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistics
Statistics (from German language, German: ', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of statistical survey, surveys and experimental design, experiments. When census data (comprising every member of the target population) cannot be collected, statisticians collect data by developing specific experiment designs and survey sample (statistics), samples. Representative sampling assures that inferences and conclusions can reasonably extend from the sample ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Punched Card
A punched card (also punch card or punched-card) is a stiff paper-based medium used to store digital information via the presence or absence of holes in predefined positions. Developed over the 18th to 20th centuries, punched cards were widely used for data processing, the control of automated machines, and computing. Early applications included controlling weaving looms and recording census data. Punched cards were widely used in the 20th century, where unit record equipment, unit record machines, organized into data processing systems, used punched cards for Input (computer science), data input, data output, and data storage. The IBM 12-row/80-column punched card format came to dominate the industry. Many early digital computers used punched cards as the primary medium for input of both computer programs and Data (computing), data. Punched cards were used for decades before being replaced by magnetic storage and terminals. Their influence persists in cultural references, sta ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Expectation–maximization Algorithm
In statistics, an expectation–maximization (EM) algorithm is an iterative method to find (local) maximum likelihood or maximum a posteriori (MAP) estimates of parameters in statistical models, where the model depends on unobserved latent variables. The EM iteration alternates between performing an expectation (E) step, which creates a function for the expectation of the log-likelihood evaluated using the current estimate for the parameters, and a maximization (M) step, which computes parameters maximizing the expected log-likelihood found on the ''E'' step. These parameter-estimates are then used to determine the distribution of the latent variables in the next E step. It can be used, for example, to estimate a mixture of gaussians, or to solve the multiple linear regression problem. History The EM algorithm was explained and given its name in a classic 1977 paper by Arthur Dempster, Nan Laird, and Donald Rubin. They pointed out that the method had been "proposed man ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Censoring (statistics)
In statistics, censoring is a condition in which the Value (mathematics), value of a measurement or observation is only partially known. For example, suppose a study is conducted to measure the impact of a drug on mortality rate. In such a study, it may be known that an individual's age at death is ''at least'' 75 years (but may be more). Such a situation could occur if the individual withdrew from the study at age 75, or if the individual is currently alive at the age of 75. Censoring also occurs when a value occurs outside the range of a measuring instrument. For example, a bathroom scale might only measure up to 140 kg, after which it rolls over 0 and continues to count up from there. If a 160 kg individual is weighed using the scale, the observer would only know that the individual's weight is 20 modulo, mod 140 kg (in addition to 160kg, they could weigh 20kg, 300kg, 440kg, and so on). The problem of censored data, in which the observed value of some variable is partially kn ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bootstrapping (statistics)
Bootstrapping is a procedure for estimating the distribution of an estimator by resampling (often with replacement) one's data or a model estimated from the data. Bootstrapping assigns measures of accuracy ( bias, variance, confidence intervals, prediction error, etc.) to sample estimates.software This technique allows estimation of the sampling distribution of almost any statistic using random sampling methods. Bootstrapping estimates the properties of an estimand (such as its ) by measuring those properties when sampling from an approximating distribution. One standard choice for an approximating distributi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
R (programming Language)
R is a programming language for statistical computing and Data and information visualization, data visualization. It has been widely adopted in the fields of data mining, bioinformatics, data analysis, and data science. The core R language is extended by a large number of R package, software packages, which contain Reusability, reusable code, documentation, and sample data. Some of the most popular R packages are in the tidyverse collection, which enhances functionality for visualizing, transforming, and modelling data, as well as improves the ease of programming (according to the authors and users). R is free and open-source software distributed under the GNU General Public License. The language is implemented primarily in C (programming language), C, Fortran, and Self-hosting (compilers), R itself. Preprocessor, Precompiled executables are available for the major operating systems (including Linux, MacOS, and Microsoft Windows). Its core is an interpreted language with a na ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
List Of Statistical Software
The following is a list of statistical software. Open-source * ADaMSoft – a generalized statistical software with data mining algorithms and methods for data management * ADMB – a software suite for non-linear statistical modeling based on C++ which uses automatic differentiation * Chronux – for neurobiological time series data * DAP – free replacement for SAS * Environment for DeveLoping KDD-Applications Supported by Index-Structures (ELKI) a software framework for developing data mining algorithms in Java * Epi Info – statistical software for epidemiology developed by Centers for Disease Control and Prevention (CDC). Apache 2 licensed * Fityk – nonlinear regression software (GUI and command line) * GNU Octave – programming language very similar to MATLAB with statistical features * gretl – gnu regression, econometrics and time-series library * intrinsic Noise Analyzer (iNA) – For analyzing intrinsic fluctuations in biochemical systems * jamovi – A fr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
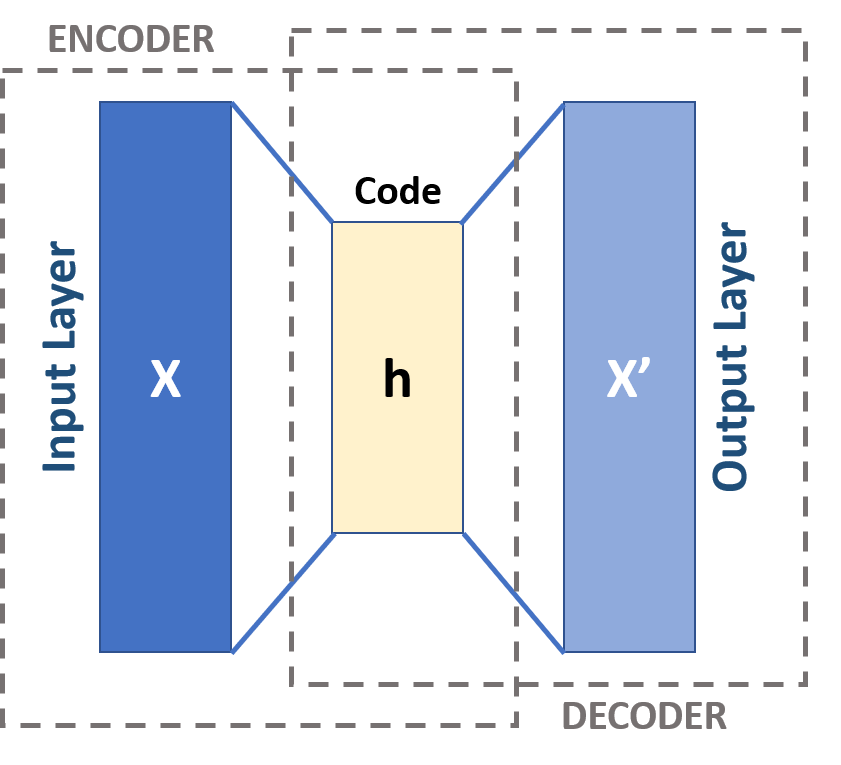
Autoencoder
An autoencoder is a type of artificial neural network used to learn efficient codings of unlabeled data (unsupervised learning). An autoencoder learns two functions: an encoding function that transforms the input data, and a decoding function that recreates the input data from the encoded representation. The autoencoder learns an efficient representation (encoding) for a set of data, typically for dimensionality reduction, to generate lower-dimensional embeddings for subsequent use by other machine learning algorithms. Variants exist which aim to make the learned representations assume useful properties. Examples are regularized autoencoders (''sparse'', ''denoising'' and ''contractive'' autoencoders), which are effective in learning representations for subsequent classification tasks, and ''variational'' autoencoders, which can be used as generative models. Autoencoders are applied to many problems, including facial recognition, feature detection, anomaly detection, and l ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Missing Data
In statistics, missing data, or missing values, occur when no data value is stored for the variable in an observation. Missing data are a common occurrence and can have a significant effect on the conclusions that can be drawn from the data. Missing data can occur because of nonresponse: no information is provided for one or more items or for a whole unit ("subject"). Some items are more likely to generate a nonresponse than others: for example items about private subjects such as income. Attrition is a type of missingness that can occur in longitudinal studies—for instance studying development where a measurement is repeated after a certain period of time. Missingness occurs when participants drop out before the test ends and one or more measurements are missing. Data often are missing in research in economics, sociology, and political science because governments or private entities choose not to, or fail to, report critical statistics, or because the information is not avai ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stochastic
Stochastic (; ) is the property of being well-described by a random probability distribution. ''Stochasticity'' and ''randomness'' are technically distinct concepts: the former refers to a modeling approach, while the latter describes phenomena; in everyday conversation, however, these terms are often used interchangeably. In probability theory, the formal concept of a '' stochastic process'' is also referred to as a ''random process''. Stochasticity is used in many different fields, including image processing, signal processing, computer science, information theory, telecommunications, chemistry, ecology, neuroscience, physics, and cryptography. It is also used in finance (e.g., stochastic oscillator), due to seemingly random changes in the different markets within the financial sector and in medicine, linguistics, music, media, colour theory, botany, manufacturing and geomorphology. Etymology The word ''stochastic'' in English was originally used as an adjective with the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Variance
In probability theory and statistics, variance is the expected value of the squared deviation from the mean of a random variable. The standard deviation (SD) is obtained as the square root of the variance. Variance is a measure of dispersion, meaning it is a measure of how far a set of numbers is spread out from their average value. It is the second central moment of a distribution, and the covariance of the random variable with itself, and it is often represented by \sigma^2, s^2, \operatorname(X), V(X), or \mathbb(X). An advantage of variance as a measure of dispersion is that it is more amenable to algebraic manipulation than other measures of dispersion such as the expected absolute deviation; for example, the variance of a sum of uncorrelated random variables is equal to the sum of their variances. A disadvantage of the variance for practical applications is that, unlike the standard deviation, its units differ from the random variable, which is why the standard devi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Error Term
In mathematics and statistics, an error term is an additive type of error. In writing, an error term is an instance of faulty language or grammar. Common examples include: * errors and residuals in statistics, e.g. in linear regression * the error term in numerical integration In analysis, numerical integration comprises a broad family of algorithms for calculating the numerical value of a definite integral. The term numerical quadrature (often abbreviated to quadrature) is more or less a synonym for "numerical integr ... {{sia, mathematics Error measures ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |