|
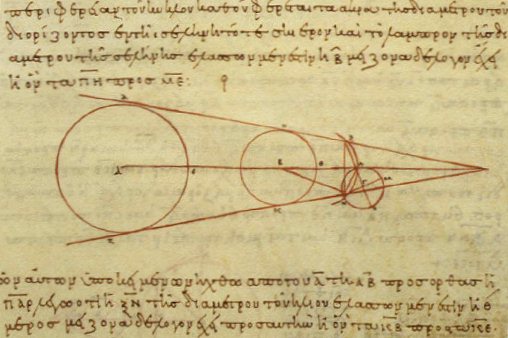
Hipparchus (cavalry Officer)
Hipparchus (; , ; BC) was a Greek astronomer, geographer, and mathematician. He is considered the founder of trigonometry, but is most famous for his incidental discovery of the precession of the equinoxes. Hipparchus was born in Nicaea, Bithynia, and probably died on the island of Rhodes, Greece. He is known to have been a working astronomer between 162 and 127 BC. Hipparchus is considered the greatest ancient astronomical observer and, by some, the greatest overall astronomer of antiquity. He was the first whose quantitative and accurate models for the motion of the Sun and Moon survive. For this he certainly made use of the observations and perhaps the mathematical techniques accumulated over centuries by the Babylonians and by Meton of Athens (fifth century BC), Timocharis, Aristyllus, Aristarchus of Samos, and Eratosthenes, among others. He developed trigonometry and constructed trigonometric tables, and he solved several problems of spherical trigonom ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Engraved Gem
An engraved gem, frequently referred to as an intaglio, is a small and usually semi-precious gemstone that has been carved, in the Western tradition normally with images or inscriptions only on one face. The engraving of gemstones was a major luxury art form in the Ancient history, ancient world, and an important one in some later periods. Strictly speaking, ''engraving'' means carving ''in intaglio'' (with the design cut ''into'' the flat background of the stone), but relief carvings (with the design projecting ''out of'' the background as in nearly all cameo (carving), cameos) are also covered by the term. This article uses ''cameo'' in its strict sense, to denote a carving exploiting layers of differently coloured stone. The activity is also called ''gem carving'' and the artists ''gem-cutters''. References to antique gems and intaglios in a jewellery context will almost always mean carved gems; when referring to monumental sculpture, the term counter-relief, meaning the same a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Precession Of The Equinoxes
In astronomy, axial precession is a gravity-induced, slow, and continuous change in the orientation of an astronomical body's Rotation around a fixed axis, rotational axis. In the absence of precession, the astronomical body's orbit would show axial parallelism. In particular, axial precession can refer to the gradual shift in the orientation of Earth's axis of rotation in a cycle of approximately 26,000 years.Hohenkerk, C.Y., Yallop, B.D., Smith, C.A., & Sinclair, A.T. "Celestial Reference Systems" in Seidelmann, P.K. (ed.) ''Explanatory Supplement to the Astronomical Almanac''. Sausalito: University Science Books. p. 99. This is similar to the precession of a spinning top, with the axis tracing out a pair of Cone (geometry), cones joined at their Apex (geometry), apices. The term "precession" typically refers only to this largest part of the motion; other changes in the alignment of Earth's axis—astronomical nutation, nutation and polar motion—are much smaller in magnitude ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Solar Eclipse
A solar eclipse occurs when the Moon passes between Earth and the Sun, thereby obscuring the view of the Sun from a small part of Earth, totally or partially. Such an alignment occurs approximately every six months, during the eclipse season in its new moon phase, when the Moon's orbital plane is closest to Ecliptic, the plane of Earth's orbit. In a total eclipse, the disk of the Sun is fully obscured by the Moon. In #Types, partial and annular eclipses, only part of the Sun is obscured. Unlike a lunar eclipse, which may be viewed from anywhere on the night side of Earth, a solar eclipse can only be viewed from a relatively small area of the world. As such, although total solar eclipses occur somewhere on Earth every 18 months on average, they recur at any given place only once every 360 to 410 years. If the Moon were in a perfectly circular orbit and in the same orbital plane as Earth, there would be total solar eclipses once a month, at every new moon. Instead, because the Mo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lunar Theory
Lunar theory attempts to account for the motions of the Moon. There are many small variations (or perturbation (astronomy), perturbations) in the Moon's motion, and many attempts have been made to account for them. After centuries of being problematic, lunar motion can now be modeled to a very high degree of accuracy (see section #Modern developments, Modern developments). Lunar theory includes: * the background of general theory; including mathematical techniques used to analyze the Moon's motion and to generate formulae and algorithms for predicting its movements; and also * quantitative formulae, algorithms, and geometrical diagrams that may be used to compute the Moon's position for a given time; often by the help of tables based on the algorithms. Lunar theory has a history of over 2000 years of investigation. Its more modern developments have been used over the last three centuries for fundamental scientific and technological purposes, and are still being used in that way. A ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spherical Trigonometry
Spherical trigonometry is the branch of spherical geometry that deals with the metrical relationships between the edge (geometry), sides and angles of spherical triangles, traditionally expressed using trigonometric functions. On the sphere, geodesics are great circles. Spherical trigonometry is of great importance for calculations in astronomy, geodesy, and navigation. The origins of spherical trigonometry in Greek mathematics and the major developments in Islamic mathematics are discussed fully in History of trigonometry and Mathematics in medieval Islam. The subject came to fruition in Early Modern times with important developments by John Napier, Jean Baptiste Joseph Delambre, Delambre and others, and attained an essentially complete form by the end of the nineteenth century with the publication of Todhunter's textbook ''Spherical trigonometry for the use of colleges and Schools''. Since then, significant developments have been the application of vector methods, quaternion m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trigonometric Tables
In mathematics, tables of trigonometric functions are useful in a number of areas. Before the existence of pocket calculators, trigonometric tables were essential for navigation, science and engineering. The calculation of mathematical tables was an important area of study, which led to the development of the first mechanical computing devices. Modern computers and pocket calculators now generate trigonometric function values on demand, using special libraries of mathematical code. Often, these libraries use pre-calculated tables internally, and compute the required value by using an appropriate interpolation method. Interpolation of simple look-up tables of trigonometric functions is still used in computer graphics, where only modest accuracy may be required and speed is often paramount. Another important application of trigonometric tables and generation schemes is for fast Fourier transform (FFT) algorithms, where the same trigonometric function values (called ''twiddle fa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eratosthenes
Eratosthenes of Cyrene (; ; – ) was an Ancient Greek polymath: a Greek mathematics, mathematician, geographer, poet, astronomer, and music theory, music theorist. He was a man of learning, becoming the chief librarian at the Library of Alexandria. His work is comparable to the study of geography, and he introduced some of the terminology, even coining the terms geography and geographer. He is best known for being the first person known to calculate the Earth's circumference, which he did by using the extensive survey results he could access in his role at the Library. His calculation was remarkably accurate (his error margin turned out to be less than 1%). He was the first to calculate Earth's axial tilt, which similarly proved to have remarkable accuracy. He created the Eratosthenes' Map of the World, first global projection of the world, incorporating Circle of latitude, parallels and Longitude, meridians based on the available geographic knowledge of his era. Eratosth ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Aristarchus Of Samos
Aristarchus of Samos (; , ; ) was an ancient Greek astronomer and mathematician who presented the first known heliocentric model that placed the Sun at the center of the universe, with the Earth revolving around the Sun once a year and rotating about its axis once a day. He also supported the theory of Anaxagoras according to which the Sun was just another star. He likely moved to Alexandria, and he was a student of Strato of Lampsacus, who later became the third head of the Peripatetic school in Greece. According to Ptolemy, he observed the summer solstice of 280 BC. Along with his contributions to the heliocentric model, as reported by Vitruvius, he created two separate sundials: one that is a flat disc; and one hemispherical. Aristarchus estimated the sizes of the Sun and Moon as compared to Earth's size. He also estimated the distances from the Earth to the Sun and Moon. His estimate that the Sun was 7 times larger than Earth (while inaccurate by an order of magnitu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Aristyllus
Aristyllus (; fl. c. 261 BC) was a Greek astronomer, presumably of the school of Timocharis (c. 300 BC). He was among the earliest meridian-astronomy observers. Six of his stellar declinations are preserved at Almajest 7.3. All are exactly correct within his over-cautious rounding to 1/4 degree. See discussion (and lessons) aDIO 7.1‡1 p. 13 (2007). Aristyllus was long mis-dated to c. 300 BC (which made his data look among the poorest of the ancients); but when his correct date was found by least-squares (Isis 73:259-265 982p. 263), it warealizedthat his star declinations' accuracy was unexcelled in antiquity. His data suggest that he worked in Alexandria: seDIO 4.1‡3 Table 3 p. 45 (2004). A lunar crater, Aristillus, aptly near the Moon's meridian and at a lunar latitude roughly equal to the terrestrial latitude of Alexandria, is named after him. Sources * Thomas Hockey's '' Biographical Encyclopedia of Astronomers'' provides the following in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Timocharis
Timocharis of Alexandria ( or Τιμοχάρης, ''gen.'' Τιμοχάρους; c. 320–260 BC) was a Greek astronomer and philosopher. Likely born in Alexandria, he was a contemporary of Euclid. Work What little is known about Timocharis comes from citations by Ptolemy in the '' Almagest''. These indicate that Timocharis worked in Alexandria during the 290s and 280s BC. Ptolemy lists the declination of 18 stars as recorded by Timocharis or Aristillus in roughly the year 290 BC. Between 295 and 272 BC, Timocharis recorded four lunar occultations and the passage of the planet Venus across a star. These were recorded using both the Egyptian and Athenian calendars. The observed stellar passage by Venus may have occurred on October 12, 272 BC when the planet came within 15 arcminutes of the star η Virginis. The observations by Timocharis are among the oldest Greek records that can be assigned a specific date. They are only exceeded by records of the summer solstice of 432 BC, as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Meton Of Athens
Meton of Athens (; ''gen''.: Μέτωνος) was a Greek mathematician, astronomer, geometer, and engineer who lived in Athens in the 5th century BC. He is best known for calculations involving the eponymous 19-year Metonic cycle, which he introduced in 432 BC into the lunisolar Attic calendar. Euphronios says that Colonus was Meton's deme. Work The Metonic calendar incorporates knowledge that 19 solar years and 235 lunar months are very nearly of the same duration. Consequently, a given day of a lunar month will often occur on the same day of the solar year as it did 19 years previously. Meton's observations were made in collaboration with Euctemon, about whom nothing else is known. The Greek astronomer Callippus expanded on the work of Meton, proposing what is now called the Callippic cycle. A Callippic cycle runs for 76 years, or four Metonic cycles. Callippus refined the lunisolar calendar, deducting one day from the fourth Metonic cycle in each Callippic cycle (i. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Babylonia
Babylonia (; , ) was an Ancient history, ancient Akkadian language, Akkadian-speaking state and cultural area based in the city of Babylon in central-southern Mesopotamia (present-day Iraq and parts of Kuwait, Syria and Iran). It emerged as an Akkadian-populated but Amorites, Amorite-ruled state . During the reign of Hammurabi and afterwards, Babylonia was retrospectively called "the country of Akkad" ( in Akkadian), a deliberate archaism in reference to the previous glory of the Akkadian Empire. It was often involved in rivalry with the older ethno-linguistically related state of Assyria in the north of Mesopotamia and Elam to the east in Ancient Iran. Babylonia briefly became the major power in the region after Hammurabi (floruit, fl. –1752 BC middle chronology, or –1654 BC, short chronology timeline, short chronology) created a short-lived empire, succeeding the earlier Akkadian Empire, Third Dynasty of Ur, and Old Assyrian Empire. The Babylonian Empire rapidly fell apar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |