|
Hexecontahedron
In geometry, a hexecontahedron (or hexacontahedron) is a polyhedron with 60 faces. There are many symmetric forms, and the ones with highest symmetry have icosahedral symmetry: Four Catalan solids, convex: * Pentakis dodecahedron - isosceles triangles * Deltoidal hexecontahedron - kites * Pentagonal hexecontahedron - pentagons * Triakis icosahedron - isosceles triangles Concave * Rhombic hexecontahedron - rhombi 27 uniform star-polyhedral duals: (self-intersecting) *Small dodecicosacron, Great dodecicosacron *Small rhombidodecacron, Great rhombidodecacron *Small dodecacronic hexecontahedron, Great dodecacronic hexecontahedron *Rhombicosacron *Small icosacronic hexecontahedron, Medial icosacronic hexecontahedron, Great icosacronic hexecontahedron *Small stellapentakis dodecahedron, Great stellapentakis dodecahedron *Great pentakis dodecahedron *Great triakis icosahedron *Small ditrigonal dodecacronic hexecontahedron, Great ditrigonal dodecacronic hexecontahedron *Medial deltoid ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Deltoidal Hexecontahedron
In geometry, a deltoidal hexecontahedron (also sometimes called a ''trapezoidal hexecontahedron'', a ''strombic hexecontahedron'', or a ''tetragonal hexacontahedron'') is a Catalan solid which is the dual polyhedron of the rhombicosidodecahedron, an Archimedean solid. It is one of six Catalan solids to not have a Hamiltonian path among its vertices. It is topologically identical to the nonconvex rhombic hexecontahedron. Lengths and angles The 60 faces are deltoids or kites. The short and long edges of each kite are in the ratio 1: ≈ 1:1.539344663... The angle between two short edges in a single face is arccos()≈118.2686774705°. The opposite angle, between long edges, is arccos()≈67.783011547435° . The other two angles of each face, between a short and a long edge each, are both equal to arccos()≈86.97415549104°. The dihedral angle between any pair of adjacent faces is arccos()≈154.12136312578°. Topology Topologically, the ''deltoidal hexecontahedron'' is ident ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
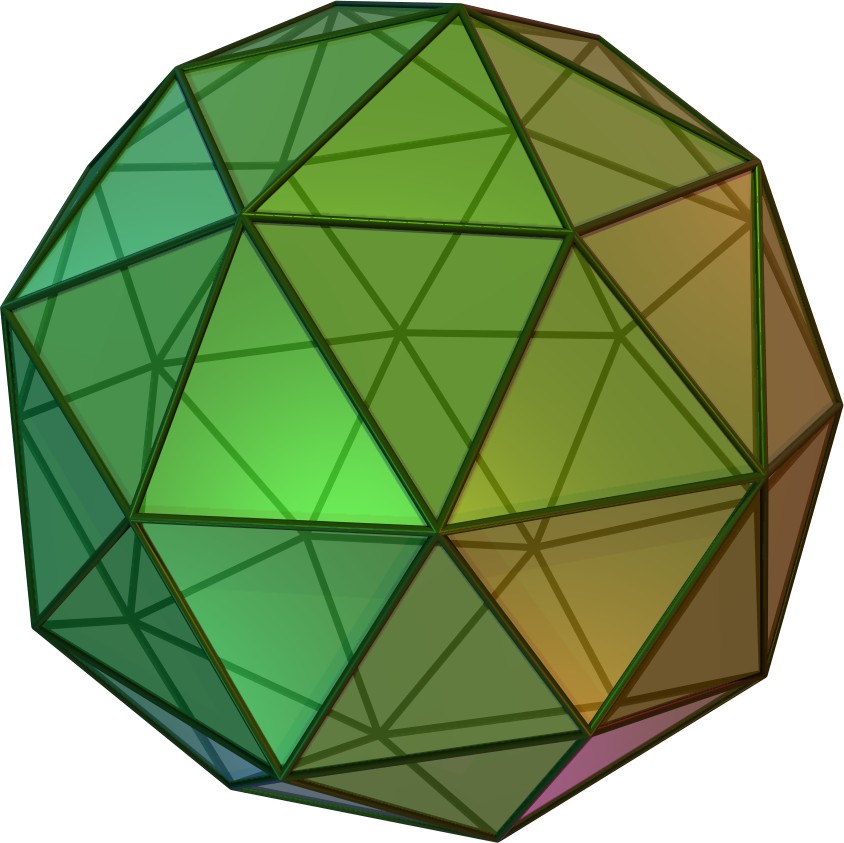
Pentagonal Hexecontahedron
In geometry, a pentagonal hexecontahedron is a Catalan solid, dual of the snub dodecahedron. It has two distinct forms, which are mirror images (or "enantiomorphs") of each other. It has 92 vertices that span 60 pentagonal faces. It is the Catalan solid with the most vertices. Among the Catalan and Archimedean solids, it has the second largest number of vertices, after the truncated icosidodecahedron, which has 120 vertices. Construction The pentagonal hexecontahedron can be constructed from a snub dodecahedron without taking the dual. Pentagonal pyramids are added to the 12 pentagonal faces of the snub dodecahedron, and triangular pyramids are added to the 20 triangular faces that do not share an edge with a pentagon. The pyramid heights are adjusted to make them coplanar with the other 60 triangular faces of the snub dodecahedron. The result is the pentagonal hexecontahedron. Geometry The faces are irregular pentagons with two long edges and three short edges. Let \xi\appr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rhombic Hexecontahedron
In geometry, a rhombic hexecontahedron is a stellation of the rhombic triacontahedron. It is nonconvex with 60 golden rhombic faces with icosahedral symmetry. It was described mathematically in 1940 by Helmut Unkelbach. It is topologically identical to the convex deltoidal hexecontahedron which has kite faces. Dissection The rhombic hexecontahedron can be dissected into 20 acute golden rhombohedra meeting at a central point. This gives the volume of a hexecontahedron of side length ''a'' to be V = (10 + 2\sqrt 5)a^3 and the area to be A = (24\sqrt 5)a^2. : Construction A rhombic hexecontahedron can be constructed from a regular dodecahedron, by taking its vertices, its face centers and its edge centers and scaling them in or out from the body center to different extents. Thus, if the 20 vertices of a dodecahedron are pulled out to increase the circumradius by a factor of ( ϕ+1)/2 ≈ 1.309, the 12 face centers are pushed in to decrease the inradius to (3-ϕ)/2 ≈ 0.691 o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Catalan Solid
In mathematics, a Catalan solid, or Archimedean dual, is a dual polyhedron to an Archimedean solid. There are 13 Catalan solids. They are named for the Belgian mathematician Eugène Catalan, who first described them in 1865. The Catalan solids are all convex. They are face-transitive but not vertex-transitive. This is because the dual Archimedean solids are vertex-transitive and not face-transitive. Note that unlike Platonic solids and Archimedean solids, the faces of Catalan solids are ''not'' regular polygons. However, the vertex figures of Catalan solids are regular, and they have constant dihedral angles. Being face-transitive, Catalan solids are isohedra. Additionally, two of the Catalan solids are edge-transitive: the rhombic dodecahedron and the rhombic triacontahedron. These are the duals of the two quasi-regular Archimedean solids. Just as prisms and antiprisms are generally not considered Archimedean solids, so bipyramids and trapezohedra are generally n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Small Hexagonal Hexecontahedron
In geometry, the small hexagonal hexecontahedron is a nonconvex isohedral polyhedron. It is the dual of the uniform small snub icosicosidodecahedron. It is partially degenerate, having coincident vertices, as its dual has coplanar triangular faces. Geometry Treating it as a simple non-convex solid (without intersecting surfaces), it has 180 faces (all triangles), 270 edges, and 92 vertices (twelve with degree 10, twenty with degree 12, and sixty with degree 3), giving an Euler characteristic of 92 − 270 + 180 = +2. Faces The faces are irregular hexagons with two short and four long edges. Denoting the golden ratio by \phi and putting \xi = \frac-\frac\sqrt\approx -0.433\,380\,199\,59, the hexagons have five equal angles of \arccos(\xi)\approx 115.682\,268\,170\,75^ and one of \arccos(\phi^\xi-\phi^)\approx 141.588\,659\,146\,23^. Each face has four long and two short edges. The ratio between the edge lengths is :1/2 +1/2\times\sqrt\approx 0.777\,024\,337\,46. The dihedr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Great Ditrigonal Dodecacronic Hexecontahedron
In geometry, the great ditrigonal dodecacronic hexecontahedron (or great lanceal trisicosahedron) is a nonconvex isohedral polyhedron. It is the dual of the uniform great ditrigonal dodecicosidodecahedron. Its faces are kites. Part of each kite lies inside the solid, hence is invisible in solid models. Proportions Kite faces have two angles of \arccos(\frac-\frac\sqrt)\approx 98.183\,872\,491\,81^, one of \arccos(-\frac+\frac\sqrt)\approx 112.296\,452\,073\,54^ and one of \arccos(-\frac+\frac\sqrt)\approx 51.335\,802\,942\,83^. Its dihedral angles A dihedral angle is the angle between two intersecting planes or half-planes. In chemistry, it is the clockwise angle between half-planes through two sets of three atoms, having two atoms in common. In solid geometry, it is defined as the un ... equal \arccos()\approx 127.686\,523\,427\,48^. The ratio between the lengths of the long edges and the short ones equals \frac\approx 1.917\,288\,176\,70. References * p. 62 E ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Small Ditrigonal Dodecacronic Hexecontahedron
In geometry, the small ditrigonal dodecacronic hexecontahedron (or fat star) is a nonconvex isohedral polyhedron. It is the dual of the uniform small ditrigonal dodecicosidodecahedron. It is visually identical to the small dodecicosacron. Its faces are darts. A part of each dart lies inside the solid, hence is invisible in solid models. Proportions Faces have two angles of \arccos(\frac+\frac\sqrt)\approx 12.661\,078\,804\,43^, one of \arccos(-\frac-\frac\sqrt)\approx 116.996\,396\,851\,70^ and one of 360^-\arccos(-\frac-\frac\sqrt)\approx 217.681\,445\,539\,45^. Its dihedral angles A dihedral angle is the angle between two intersecting planes or half-planes. In chemistry, it is the clockwise angle between half-planes through two sets of three atoms, having two atoms in common. In solid geometry, it is defined as the un ... equal \arccos()\approx 146.230\,659\,755\,53^. The ratio between the lengths of the long and short edges is \frac\approx 1.110\,008\,944\,41. Ref ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Great Icosacronic Hexecontahedron
In geometry, the great icosacronic hexecontahedron (or great sagittal trisicosahedron) is the dual of the great icosicosidodecahedron. Its faces are darts. A part of each dart lies inside the solid, hence is invisible in solid models. Proportions Faces have two angles of \arccos(\frac+\frac\sqrt)\approx 30.480\,324\,565\,36^, one of \arccos(-\frac+\frac\sqrt)\approx 51.335\,802\,942\,83^ and one of 360^-\arccos(-\frac+\frac\sqrt)\approx 247.703\,547\,926\,46^. Its dihedral angles A dihedral angle is the angle between two intersecting planes or half-planes. In chemistry, it is the clockwise angle between half-planes through two sets of three atoms, having two atoms in common. In solid geometry, it is defined as the un ... equal \arccos()\approx 127.686\,523\,427\,48^. The ratio between the lengths of the long and short edges is \frac\approx 1.917\,288\,176\,70. References * External links Dual uniform polyhedra {{polyhedron-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Medial Icosacronic Hexecontahedron
In geometry, the medial icosacronic hexecontahedron (or midly sagittal ditriacontahedron) is a nonconvex isohedral polyhedron. It is the dual of the uniform icosidodecadodecahedron. Its faces are darts. Part of each dart lies inside the solid, hence is invisible in solid models. Proportions Faces have two angles of \arccos(\frac)\approx 41.409\,622\,109\,27^, one of \arccos(-\frac+\frac\sqrt)\approx 58.184\,446\,117\,59^ and one of 360^-\arccos(-\frac-\frac\sqrt)\approx 218.996\,309\,663\,87^. Its dihedral angles A dihedral angle is the angle between two intersecting planes or half-planes. In chemistry, it is the clockwise angle between half-planes through two sets of three atoms, having two atoms in common. In solid geometry, it is defined as the un ... equal \arccos(-\frac)\approx 135.584\,691\,402\,81^. The ratio between the lengths of the long and short edges is \frac\approx 1.938\,748\,901\,93. References * External links * Dual uniform polyhedra {{poly ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Small Icosacronic Hexecontahedron
In geometry, the small icosacronic hexecontahedron (or small lanceal trisicosahedron) is a nonconvex isohedral polyhedron. It is the dual of the uniform small icosicosidodecahedron. Its faces are kites. Part of each kite lies inside the solid, hence is invisible in solid models. Proportions The kites have two angles of \arccos(\frac-\frac\sqrt)\approx 50.342\,524\,343\,87^, one of \arccos(-\frac-\frac\sqrt)\approx 142.318\,554\,460\,55^ and one of \arccos(-\frac-\frac\sqrt)\approx 116.996\,396\,851\,70^. The dihedral angle A dihedral angle is the angle between two intersecting planes or half-planes. In chemistry, it is the clockwise angle between half-planes through two sets of three atoms, having two atoms in common. In solid geometry, it is defined as the un ... equals \arccos(\frac)\approx 146.230\,659\,755\,53^. The ratio between the lengths of the long and short edges is \frac\approx 1.110\,008\,944\,41. References * External links * Dual uniform polyhedra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Great Dodecacronic Hexecontahedron
In geometry, the great dodecacronic hexecontahedron (or great lanceal ditriacontahedron) is a nonconvex isohedral polyhedron. It is the dual of the uniform great dodecicosidodecahedron. Its 60 intersecting quadrilateral faces are kites. Part of each kite lies inside the solid, hence is invisible in solid models. Proportions Each kite has two angles of \arccos(\frac-\frac\sqrt)\approx 69.788\,198\,194\,11^, one of \arccos(-\frac+\frac\sqrt)\approx 91.512\,394\,720\,74^ and one of \arccos(-\frac-\frac\sqrt)\approx 128.911\,208\,891\,04^. The dihedral angle A dihedral angle is the angle between two intersecting planes or half-planes. In chemistry, it is the clockwise angle between half-planes through two sets of three atoms, having two atoms in common. In solid geometry, it is defined as the un ... equals \arccos(\frac)\approx 91.553\,403\,672\,16^. The ratio between the lengths of the long and short edges is \frac\approx 1.259\,463\,815\,11. References * External links ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Small Dodecacronic Hexecontahedron
In geometry, the small dodecicosidodecahedron (or small dodekicosidodecahedron) is a nonconvex uniform polyhedron, indexed as U33. It has 44 faces (20 triangles, 12 pentagons, and 12 decagons), 120 edges, and 60 vertices. Its vertex figure is a crossed quadrilateral. Related polyhedra It shares its vertex arrangement with the small stellated truncated dodecahedron and the uniform compounds of 6 or 12 pentagrammic prisms. It additionally shares its edge arrangement with the rhombicosidodecahedron (having the triangular and pentagonal faces in common), and with the small rhombidodecahedron (having the decagonal faces in common). Dual The dual polyhedron to the small dodecicosidodecahedron is the small dodecacronic hexecontahedron (or small sagittal ditriacontahedron). It is visually identical to the small rhombidodecacron. Its faces are darts. A part of each dart lies inside the solid, hence is invisible in solid models. Proportions Faces have two angles of \arccos ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |