|
Gyrobicupola
In geometry, a bicupola is a solid formed by connecting two cupolae on their bases. Here, two classes of bicupola are included because each cupola (bicupola half) is bordered by alternating triangles and squares. If similar faces are attached together the result is an ''orthobicupola''; if squares are attached to triangles it is a ''gyrobicupola''. Forms Set of orthobicupolae Set of gyrobicupolae A -gonal gyrobicupola has the same topology as a -gonal rectified antiprism, Conway polyhedron notation In geometry and topology, Conway polyhedron notation, invented by John Horton Conway and promoted by George W. Hart, is used to describe polyhedra based on a seed polyhedron modified by various prefix operations. Conway and Hart extended the i ..., . References {{DEFAULTSORT:Bicupola Polyhedra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cupola (geometry)
In geometry, a cupola is a Polyhedron, solid formed by joining two polygons, one (the base) with twice as many Edge (geometry), edges as the other, by an alternating band of isosceles triangles and rectangles. If the triangles are equilateral triangle, equilateral and the rectangles are Square (geometry), squares, while the base and its opposite face are regular polygons, the triangular cupola, triangular, square cupola, square, and pentagonal cupola, pentagonal cupolae all count among the Johnson solids, and can be formed by taking sections of the cuboctahedron, rhombicuboctahedron, and rhombicosidodecahedron, respectively. A cupola can be seen as a prism (geometry), prism where one of the polygons has been collapsed in half by merging alternate vertices. A cupola can be given an extended Schläfli symbol representing a regular polygon joined by a parallel of its Truncation (geometry)#Truncation of polygons, truncation, or Cupolae are a subclass of the prismatoids. Its d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pentagonal Gyrobicupola
The pentagonal gyrobicupola is a polyhedron that is constructed by attaching two pentagonal cupolas base-to-base, each of its cupolas is twisted at 36°. It is an example of a Johnson solid and a composite polyhedron. Construction The pentagonal gyrobicupola is a composite polyhedron: it is constructed by attaching two pentagonal cupolas base-to-base. This construction is similar to the pentagonal orthobicupola; the difference is that one of cupolas in the pentagonal gyrobicupola is twisted at 36°, as suggested by the prefix ''gyro-''. The resulting polyhedron has the same faces as the pentagonal orthobicupola does: those cupolas cover their decagonal bases, replacing it with eight equilateral triangles, eight squares, and two regular pentagons. A convex polyhedron in which all of its faces are regular polygons is the Johnson solid In geometry, a Johnson solid, sometimes also known as a Johnson–Zalgaller solid, is a convex polyhedron whose faces are regular polygons. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Square Gyrobicupola
In geometry, the square gyrobicupola is one of the Johnson solids (). Like the square orthobicupola (), it can be obtained by joining two square cupolae () along their bases. The difference is that in this solid, the two halves are rotated 45 degrees with respect to one another. The ''square gyrobicupola'' is the second in an infinite set of gyrobicupolae. Related to the square gyrobicupola is the elongated square gyrobicupola. This polyhedron is created when an octagonal prism is inserted between the two halves of the square gyrobicupola. Formulae The following formulae for volume and surface area can be used if all faces are regular, with edge length ''a'': :V=\left(2+\frac\right)a^3\approx3.88562...a^3 :A=2\left(5+\sqrt\right)a^2\approx13.4641...a^2 Related polyhedra and honeycombs The square gyrobicupola forms space-filling honeycombs with tetrahedra, cubes and cuboctahedra; and with tetrahedra, square pyramids, and elongated square bipyramids. (The latter unit ca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometry
Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician who works in the field of geometry is called a ''List of geometers, geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point (geometry), point, line (geometry), line, plane (geometry), plane, distance, angle, surface (mathematics), surface, and curve, as fundamental concepts. Originally developed to model the physical world, geometry has applications in almost all sciences, and also in art, architecture, and other activities that are related to graphics. Geometry also has applications in areas of mathematics that are apparently unrelated. For example, methods of algebraic geometry are fundamental in Wiles's proof of Fermat's Last Theorem, Wiles's proof of Fermat's ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pentagonal Trapezohedron
In geometry, a pentagonal trapezohedron is the third in the infinite family of trapezohedra, face-transitive polyhedra. Its dual polyhedron is the pentagonal antiprism. As a decahedron it has ten faces which are congruent kites. It can be decomposed into two pentagonal pyramids and a regular dodecahedron in the middle. 10-sided dice The pentagonal trapezohedron was patented for use as a gaming die (i.e. "game apparatus") in 1906. These dice are used for role-playing games that use percentile-based skills; however, a twenty-sided die can be labeled with the numbers 0-9 twice to use for percentages instead. Subsequent patents on ten-sided dice have made minor refinements to the basic design by rounding or truncating the edges. This enables the die to tumble so that the outcome is less predictable. One such refinement became notorious at the 1980 Gen Con when the patent was incorrectly thought to cover ten-sided dice in general. Ten-sided dice are commonly numbered from ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tetragonal Trapezohedron
In geometry, a tetragonal trapezohedron, or deltohedron, is the second in an infinite series of trapezohedra, which are dual to the antiprisms. It has eight faces, which are congruent kites, and is dual to the square antiprism. Applications In mesh generation This shape has been used as a test case for hexahedral mesh generation,..... simplifying an earlier test case posited by mathematician Robert Schneiders in the form of a square pyramid with its boundary subdivided into 16 quadrilaterals. In this context the tetragonal trapezohedron has also been called the cubical octahedron, quadrilateral octahedron, or octagonal spindle, because it has eight quadrilateral faces and is uniquely defined as a combinatorial polyhedron by that property. Adding four cuboids to a mesh for the cubical octahedron would also give a mesh for Schneiders' pyramid. As a simply-connected polyhedron with an even number of quadrilateral faces, the cubical octahedron can be decomposed into topologica ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rhombic Dodecahedron
In geometry, the rhombic dodecahedron is a Polyhedron#Convex_polyhedra, convex polyhedron with 12 congruence (geometry), congruent rhombus, rhombic face (geometry), faces. It has 24 edge (geometry), edges, and 14 vertex (geometry), vertices of 2 types. As a Catalan solid, it is the dual polyhedron of the cuboctahedron. As a parallelohedron, the rhombic dodecahedron can be used to Honeycomb (geometry), tesselate its copies in space creating a rhombic dodecahedral honeycomb. There are some variations of the rhombic dodecahedron, one of which is the Bilinski dodecahedron. There are some stellations of the rhombic dodecahedron, one of which is the Escher's solid. The rhombic dodecahedron may also appear in nature (such as in the garnet crystal), the architectural philosophies, practical usages, and toys. As a Catalan solid Metric properties The rhombic dodecahedron is a polyhedron with twelve rhombus, rhombi, each of which long face-diagonal length is exactly \sqrt times the sho ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cuboctahedron
A cuboctahedron is a polyhedron with 8 triangular faces and 6 square faces. A cuboctahedron has 12 identical vertex (geometry), vertices, with 2 triangles and 2 squares meeting at each, and 24 identical edge (geometry), edges, each separating a triangle from a square. As such, it is a quasiregular polyhedron, i.e., an Archimedean solid that is not only vertex-transitive but also edge-transitive. It is Cuboctahedron#Radial equilateral symmetry, radially equilateral. Its dual polyhedron is the rhombic dodecahedron. Construction The cuboctahedron can be constructed in many ways: * Its construction can be started by attaching two regular triangular cupolas base-to-base. This is similar to one of the Johnson solids, triangular orthobicupola. The difference is that the triangular orthobicupola is constructed with one of the cupolas twisted so that similar polygonal faces are adjacent, whereas the cuboctahedron is not. As a result, the cuboctahedron may also called the ''triangular gyro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gyrobifastigium
In geometry, the gyrobifastigium is a polyhedron that is constructed by attaching a triangular prism to square face of another one. It is an example of a Johnson solid. It is the only Johnson solid that can tile three-dimensional space. Construction and its naming The gyrobifastigium can be constructed by attaching two triangular prisms along corresponding square faces, giving a quarter-turn to one prism. These prisms cover the square faces so the resulting polyhedron has four equilateral triangles and four squares, making eight faces in total, an octahedron. Because its faces are all regular polygons and it is convex, the gyrobifastigium is a Johnson solid, indexed as J_ . The name of the gyrobifastigium comes from the Latin ''fastigium'', meaning a sloping roof. In the standard naming convention of the Johnson solids, ''bi-'' means two solids connected at their bases, and ''gyro-'' means the two halves are twisted with respect to each other. Cartesian coordinates for the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cuboctahedron
A cuboctahedron is a polyhedron with 8 triangular faces and 6 square faces. A cuboctahedron has 12 identical vertex (geometry), vertices, with 2 triangles and 2 squares meeting at each, and 24 identical edge (geometry), edges, each separating a triangle from a square. As such, it is a quasiregular polyhedron, i.e., an Archimedean solid that is not only vertex-transitive but also edge-transitive. It is Cuboctahedron#Radial equilateral symmetry, radially equilateral. Its dual polyhedron is the rhombic dodecahedron. Construction The cuboctahedron can be constructed in many ways: * Its construction can be started by attaching two regular triangular cupolas base-to-base. This is similar to one of the Johnson solids, triangular orthobicupola. The difference is that the triangular orthobicupola is constructed with one of the cupolas twisted so that similar polygonal faces are adjacent, whereas the cuboctahedron is not. As a result, the cuboctahedron may also called the ''triangular gyro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
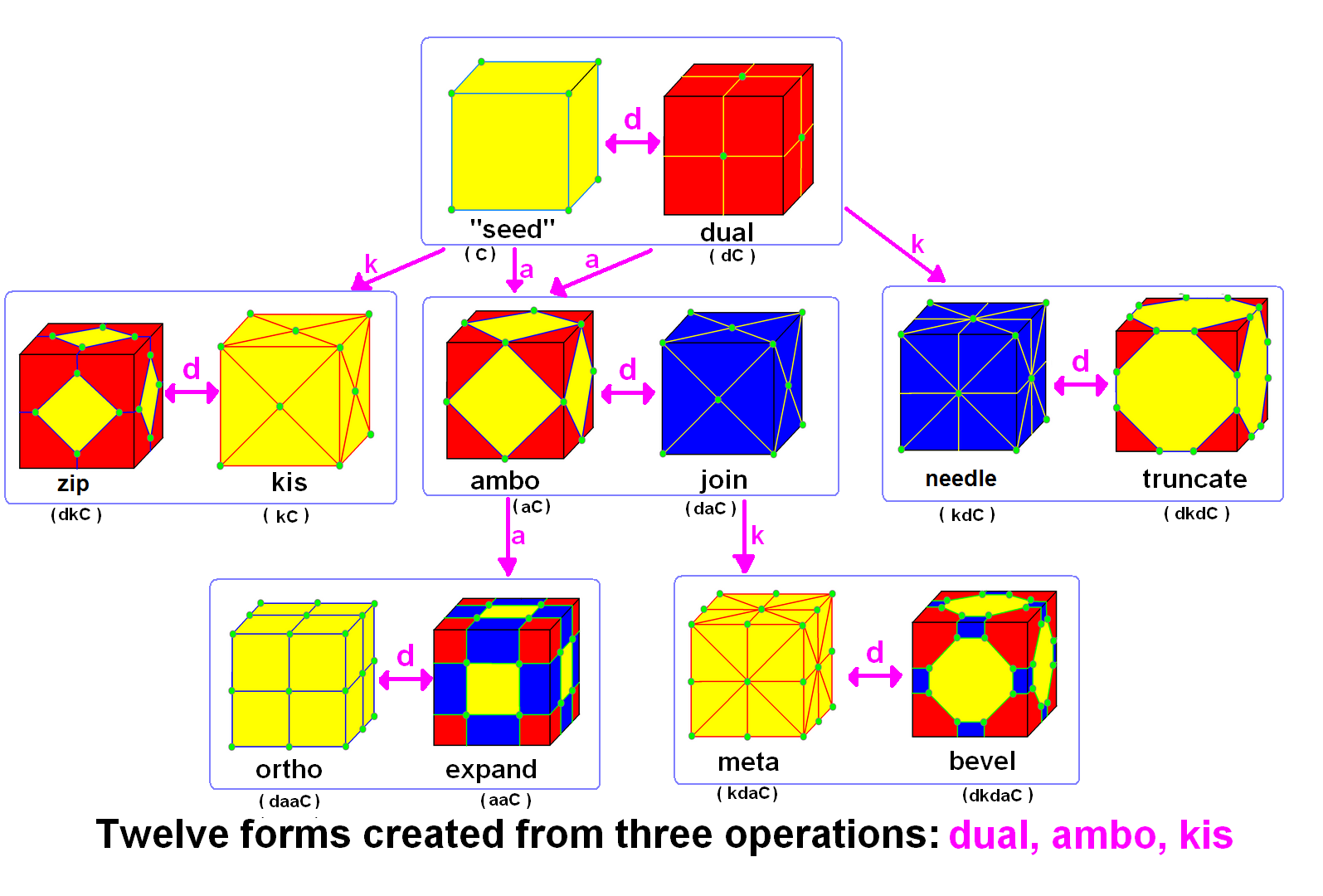
Conway Polyhedron Notation
In geometry and topology, Conway polyhedron notation, invented by John Horton Conway and promoted by George W. Hart, is used to describe polyhedra based on a seed polyhedron modified by various prefix operations. Conway and Hart extended the idea of using operators, like truncation as defined by Kepler, to build related polyhedra of the same symmetry. For example, represents a truncated cube, and , parsed as , is ( topologically) a truncated cuboctahedron. The simplest operator dual swaps vertex and face elements; e.g., a dual cube is an octahedron: . Applied in a series, these operators allow many higher order polyhedra to be generated. Conway defined the operators (ambo), (bevel), ( dual), (expand), (gyro), (join), (kis), (meta), (ortho), ( snub), and ( truncate), while Hart added ( reflect) and (propellor). Later implementations named further operators, sometimes referred to as "extended" operators. Conway's basic operations are sufficient to generate the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pentagonal Orthobicupola
In geometry, the pentagonal orthobicupola is one of the Johnson solids (). As the name suggests, it can be constructed by joining two pentagonal cupolae () along their decagonal bases, matching like faces. A 36-degree rotation of one cupola before the joining yields a pentagonal gyrobicupola (). The ''pentagonal orthobicupola'' is the third in an infinite set of orthobicupolae. Formulae The following formulae for volume and surface area can be used if all faces are regular, with edge length ''a'':Stephen Wolfram,Pentagonal orthobicupola from Wolfram Alpha WolframAlpha ( ) is an answer engine developed by Wolfram Research. It is offered as an online service that answers factual queries by computing answers from externally sourced data. History Launch preparations for WolframAlpha began on Ma .... Retrieved July 23, 2010. :V=\frac\left(5+4\sqrt\right)a^3\approx4.64809...a^3 :A=\left(10+\sqrt\right)a^2\approx17.7711...a^2 References External links * {{Polyhedron- ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |