|
Geodesic Grid
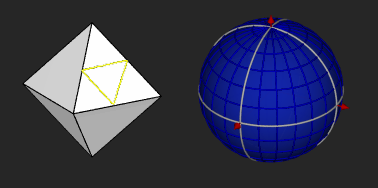
A geodesic grid is a spatial grid based on a geodesic polyhedron or Goldberg polyhedron. History The earliest use of the (icosahedral) geodesic grid in geophysical modeling dates back to 1968 and the work by Sadourny, Arakawa, and Mintz and Williamson. Later work expanded on this base. Construction A geodesic grid is a global Earth spatial reference that uses polygon tiles based on the subdivision of a polyhedron (usually the icosahedron, and usually a Class I subdivision) to subdivide the surface of the Earth. Such a grid does not have a straightforward relationship to latitude and longitude, but conforms to many of the main criteria for a statistically valid discrete global grid. Primarily, the cells' area and shape are generally similar, especially near the poles where many other spatial grids have singularities or heavy distortion. The popular Quaternary Triangular Mesh (QTM) falls into this category. Geodesic grids may use the dual polyhedron of the geodesic polyhedron, w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geodesic Grid (ISEA3H) Illustrated
In geometry, a geodesic () is a curve representing in some sense the locally shortest path ( arc) between two points in a surface, or more generally in a Riemannian manifold. The term also has meaning in any differentiable manifold with a connection. It is a generalization of the notion of a "straight line". The noun ''geodesic'' and the adjective ''geodetic'' come from ''geodesy'', the science of measuring the size and shape of Earth, though many of the underlying principles can be applied to any ellipsoidal geometry. In the original sense, a geodesic was the shortest route between two points on the Earth's surface. For a spherical Earth, it is a segment of a great circle (see also great-circle distance). The term has since been generalized to more abstract mathematical spaces; for example, in graph theory, one might consider a geodesic between two vertices/nodes of a graph. In a Riemannian manifold or submanifold, geodesics are characterised by the property of having vanish ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hex Map
A hex map, hex board, or hex grid is a game board design commonly used in simulation games of all scales, including wargames, role-playing games, and strategy games in both board games and video games. A hex map is subdivided into a hexagonal tiling, small regular hexagons of identical size. Advantages and disadvantages The primary advantage of a hex map over a traditional square grid map is that the distance between the center of each and every pair of adjacent hex cells (or ''hexes'') is the same. By comparison, in a square grid map, the distance from the center of each square cell to the center of the four diagonal adjacent cells it shares a corner with is times that of the distance to the center of the four adjacent cells it shares an edge with. This equidistant property of all adjacent hexes is desirable for games in which the measurement of movement is a factor. The other advantage is the fact that neighbouring cells always share edges; there are no two cells with co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hierarchical Triangular Mesh
Hierarchical Triangular Mesh (HTM) is a kind of Quadtree, quad tree based on subdivision of a distorted octahedron, used for mesh generation in 3D computer graphics, 3-D computer graphics and Geometric data analysis, geometric data structures. Functions * It provides a systematic indexing method for objects localized on a sphere. * It is an efficient method for searching different resolutions like Minute and second of arc, arc seconds or hemispheres. * It can be used as a method to subdivide the spherical surface into triangles of nearly equal shape and size. See also * HEALPix * Quadrilateralized spherical cube * Geodesic grid References {{algorithm-stub Mesh generators 3D graphics software that uses Qt Trees (data structures) Geometric data structures ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
HEALPix
HEALPix (sometimes written as Healpix), an acronym for Hierarchical Equal Area isoLatitude Pixelisation of a 2-sphere, is an algorithm for pixelisation of the 2-sphere based on subdivision of a distorted rhombic dodecahedron, and the associated class of map projections. The pixelisation algorithm was devised in 1997 by Krzysztof M. Górski at the Theoretical Astrophysics Center in Copenhagen, Denmark, and first published as a preprint in 1998. Projection and pixelisation The HEALPix projection is a general class of spherical projections, sharing several key properties, which map the 2-sphere to the Euclidean plane. Any of these can be followed by partitioning (pixelising) the resulting region of the 2-plane. In particular, when one of these projections (the H=4, K=3 HEALPix projection) is followed by a pixelisation of the 2-plane, the result is generally known as the HEALPix pixelisation, which is widely used in physical cosmology for maps of the cosmic microwave background. T ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polyhedral Map Projection
A polyhedral map projection is a map projection based on a spherical polyhedron. Typically, the polyhedron is overlaid on the globe, and each face of the polyhedron is transformed to a polygon or other shape in the plane. The best-known polyhedral map projection is Buckminster Fuller's Dymaxion map. When the spherical polyhedron faces are transformed to the faces of an ordinary polyhedron instead of laid flat in a plane, the result is a polyhedral globe. Often the polyhedron used is a Platonic solid or Archimedean solid. However, other polyhedra can be used: the AuthaGraph projection makes use of a polyhedron with 96 faces, and the myriahedral projection allows for an arbitrary large number of faces. Although interruptions between faces are common, and more common with an increasing number of faces, some maps avoid them: the Lee conformal projection only has interruptions at its border, and the AuthaGraph projection scales its faces so that the map fills a rectangle without int ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quadrilateralized Spherical Cube
In mapmaking, a quadrilateralized spherical cube, or quad sphere for short, is an equal-area polyhedral map projection and discrete global grid scheme for data collected on a spherical surface (either that of the Earth or the celestial sphere). It was first proposed in 1975 by Chan and O'Neill for the Naval Environmental Prediction Research Facility. This scheme is also often called the COBE sky cube, because it was designed to hold data from the Cosmic Background Explorer (COBE) project. Elements The quad sphere has two principal characteristic features. The first is that the mapping consists of projecting the sphere onto the faces of an inscribed cube using a curvilinear projection that preserves area. The sphere is divided into six equal regions, which correspond to the faces of the cube. The vertices of the cube correspond to the cartesian coordinates defined by , ''x'', =, ''y'', =, ''z'', on a sphere centred at the origin. For an Earth projection, the cube is usually o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spherical Design
A spherical design, part of combinatorial design theory in mathematics, is a finite set of ''N'' points on the ''d''-dimensional unit ''d''-sphere ''Sd'' such that the average value of any polynomial ''f'' of degree ''t'' or less on the set equals the average value of ''f'' on the whole sphere (that is, the integral of ''f'' over ''Sd'' divided by the area or measure of ''Sd''). Such a set is often called a spherical ''t''-design to indicate the value of ''t'', which is a fundamental parameter. The concept of a spherical design is due to Delsarte, Goethals, and Seidel, although these objects were understood as particular examples of cubature formulas earlier. Spherical designs can be of value in approximation theory, in statistics for experimental design, in combinatorics, and in geometry. The main problem is to find examples, given ''d'' and ''t'', that are not too large; however, such examples may be hard to come by. Spherical t-designs have also recently been appropriated in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Discrete Global Grid
A discrete global grid (DGG) is a mosaic that covers the entire Earth's surface. Mathematically it is a space partitioning: it consists of a set of non-empty regions that form a partition of the Earth's surface. In a usual grid-modeling strategy, to simplify position calculations, each region is represented by a point, abstracting the grid as a set of region-points. Each region or region-point in the grid is called a cell. When each cell of a grid is subject to a recursive partition, resulting in a "series of discrete global grids with progressively finer resolution", forming a hierarchical grid, it is called a hierarchical DGG (sometimes "global hierarchical tessellation" or "DGG system"). Discrete global grids are used as the geometric basis for the building of geospatial data structures. Each cell is related with data objects or values, or (in the hierarchical case) may be associated with other cells. DGGs have been proposed for use in a wide range of geospatial applicat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Grid Reference
A projected coordinate systemalso called a projected coordinate reference system, planar coordinate system, or grid reference systemis a type of spatial reference system that represents locations on Earth using Cartesian coordinate system, Cartesian coordinates (''x'', ''y'') on a planar surface created by a particular map projection. Each projected coordinate system, such as "Universal Transverse Mercator WGS 84 Zone 26N," is defined by a choice of map projection (with specific parameters), a choice of geodetic datum to bind the coordinate system to real locations on the earth, an origin point, and a choice of unit of measure. Hundreds of projected coordinate systems have been specified for various purposes in various regions. When the first standardized coordinate systems were created during the 20th century, such as the Universal Transverse Mercator, State Plane Coordinate System, and British National Grid, they were commonly called ''grid systems''; the term is still common ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geographic Coordinate System
A geographic coordinate system (GCS) is a spherical coordinate system, spherical or geodetic coordinates, geodetic coordinate system for measuring and communicating position (geometry), positions directly on Earth as latitude and longitude. It is the simplest, oldest, and most widely used type of the various spatial reference systems that are in use, and forms the basis for most others. Although latitude and longitude form a coordinate tuple like a cartesian coordinate system, the geographic coordinate system is not cartesian because the measurements are angles and are not on a planar surface. A full GCS specification, such as those listed in the EPSG Geodetic Parameter Dataset, EPSG and ISO 19111 standards, also includes a choice of geodetic datum (including an Earth ellipsoid), as different datums will yield different latitude and longitude values for the same location. History The invention of a geographic coordinate system is generally credited to Eratosthenes of Cy ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geodesics On An Ellipsoid
The study of geodesics on an ellipsoid arose in connection with geodesy specifically with the solution of triangulation networks. The figure of the Earth is well approximated by an '' oblate ellipsoid'', a slightly flattened sphere. A ''geodesic'' is the shortest path between two points on a curved surface, analogous to a straight line on a plane surface. The solution of a triangulation network on an ellipsoid is therefore a set of exercises in spheroidal trigonometry . If the Earth is treated as a sphere, the geodesics are great circles (all of which are closed) and the problems reduce to ones in spherical trigonometry. However, showed that the effect of the rotation of the Earth results in its resembling a slightly oblate ellipsoid: in this case, the equator and the meridians are the only simple closed geodesics. Furthermore, the shortest path between two points on the equator does not necessarily run along the equator. Finally, if the ellipsoid is further perturbed ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Square Grid
In geometry, the square tiling, square tessellation or square grid is a regular tiling of the Euclidean plane consisting of four squares around every vertex. John Horton Conway called it a quadrille. Structure and properties The square tiling has a structure consisting of one type of congruent prototile, the square, sharing two vertices with other identical ones. This is an example of monohedral tiling. Each vertex at the tiling is surrounded by four squares, which denotes in a vertex configuration as 4.4.4.4 or 4^4 . The vertices of a square can be considered as the lattice, so the square tiling can be formed through the square lattice. This tiling is commonly familiar with the flooring and game boards. It is self-dual, meaning the center of each square connects to another of the adjacent tile, forming square tiling itself. The square tiling acts transitively on the ''flags'' of the tiling. In this case, the flag consists of a mutually incident vertex, edge, and tile of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |