|
Future Value
Future value is the value of an asset at a specific date. It measures the nominal future sum of money that a given sum of money is "worth" at a specified time in the future assuming a certain interest rate, or more generally, rate of return; it is the present value multiplied by the accumulation function. Accessed: 2011-04-14. Archived by WebCite® ) The value does not include corrections for inflation or other factors that affect the true val ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Value (economics)
In economics, economic value is a measure of the benefit provided by a goods, good or service (economics), service to an Agent (economics), economic agent, and value for money represents an assessment of whether financial or other resources are being used effectively in order to secure such benefit. Economic value is generally measured through units of currency, and the interpretation is therefore "what is the maximum amount of money a person is willing and able to pay for a good or service?” Value for money is often expressed in comparative terms, such as "better", or "best value for money", but may also be expressed in absolute terms, such as where a deal does, or does not, offer value for money. Among the competing schools of economic theory there are differing Theory of value (economics), theories of value. Economic value is ''not'' the same as Price, market price, nor is economic value the same thing as market value. If a consumer is willing to buy a good, it implies tha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Simple Interest
In finance and economics, interest is payment from a debtor or deposit-taking financial institution to a lender or depositor of an amount above repayment of the principal sum (that is, the amount borrowed), at a particular rate. It is distinct from a fee which the borrower may pay to the lender or some third party. It is also distinct from dividend which is paid by a company to its shareholders (owners) from its profit or reserve, but not at a particular rate decided beforehand, rather on a pro rata basis as a share in the reward gained by risk taking entrepreneurs when the revenue earned exceeds the total costs. For example, a customer would usually pay interest to borrow from a bank, so they pay the bank an amount which is more than the amount they borrowed; or a customer may earn interest on their savings, and so they may withdraw more than they originally deposited. In the case of savings, the customer is the lender, and the bank plays the role of the borrower. Interest ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Time Value Of Money
The time value of money refers to the fact that there is normally a greater benefit to receiving a sum of money now rather than an identical sum later. It may be seen as an implication of the later-developed concept of time preference. The time value of money refers to the observation that it is better to receive money sooner than later. Money you have today can be invested to earn a positive rate of return, producing more money tomorrow. Therefore, a dollar today is worth more than a dollar in the future. The time value of money is among the factors considered when weighing the opportunity costs of spending rather than saving or investing money. As such, it is among the reasons why interest is paid or earned: interest, whether it is on a bank deposit or debt, compensates the depositor or lender for the loss of their use of their money. Investors are willing to forgo spending their money now only if they expect a favorable net rate of return, return on their investment in the fut ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
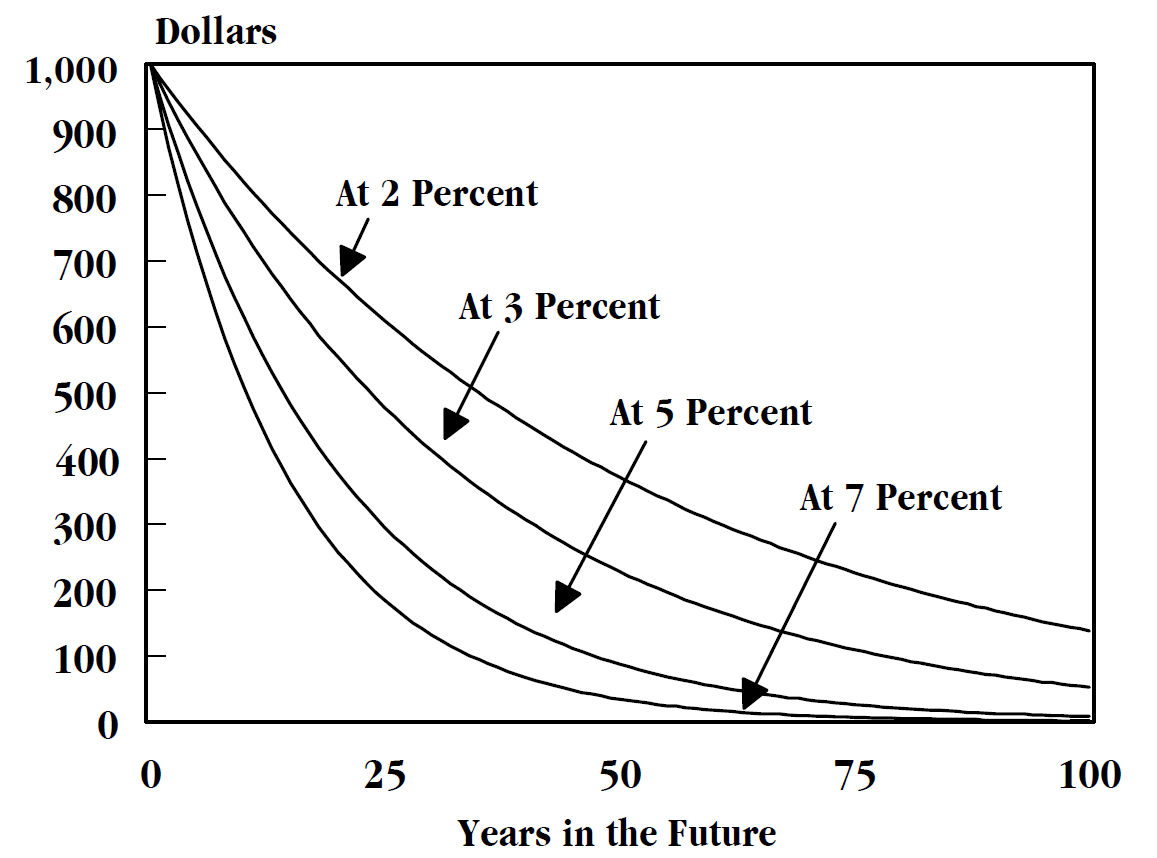
Present Value
In economics and finance, present value (PV), also known as present discounted value (PDV), is the value of an expected income stream determined as of the date of valuation. The present value is usually less than the future value because money has interest-earning potential, a characteristic referred to as the time value of money, except during times of negative interest rates, when the present value will be equal or more than the future value. Time value can be described with the simplified phrase, "A dollar today is worth more than a dollar tomorrow". Here, 'worth more' means that its value is greater than tomorrow. A dollar today is worth more than a dollar tomorrow because the dollar can be invested and earn a day's worth of interest, making the total accumulate to a value more than a dollar by tomorrow. Interest can be compared to Renting, rent. Just as rent is paid to a landlord by a tenant without the ownership of the asset being transferred, interest is paid to a lender by ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lifetime Value
In marketing, customer lifetime value (CLV or often CLTV), lifetime customer value (LCV), or life-time value (LTV) is a prognostication of the net profit contributed to the whole future relationship with a customer. The prediction model can have varying levels of sophistication and accuracy, ranging from a crude heuristic to the use of complex predictive analytics techniques. Customer lifetime value can also be defined as the monetary value of a customer relationship, based on the present value of the projected future cash flows from the customer relationship. Customer lifetime value is an important concept in that it encourages firms to shift their focus from quarterly profits to the long-term health of their customer relationships. Customer lifetime value is an important metric because it represents an upper limit on spending to acquire new customers.Farris, Paul W.; Neil T. Bendle; Phillip E. Pfeifer; David J. Reibstein (2010). ''Marketing Metrics: The Definitive Guide to M ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Annuity (finance Theory)
In investment, an annuity is a series of payments made at equal intervals based on a contract with a lump sum of money. Insurance companies are common annuity providers and are used by clients for things like retirement or death benefits. Examples of annuities are regular deposits to a savings account, monthly home mortgage payments, monthly insurance payments and pension payments. Annuities can be classified by the frequency of payment dates. The payments (deposits) may be made weekly, monthly, quarterly, yearly, or at any other regular interval of time. Annuities may be calculated by mathematical functions known as "annuity functions". An annuity which provides for payments for the remainder of a person's lifetime is a life annuity. An annuity which continues indefinitely is a perpetuity. Types Annuities may be classified in several ways. Timing of payments Payments of an ''annuity-immediate'' are made at the end of payment periods, so that interest accrues between the i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Annual Percentage Rate
The term annual percentage rate of charge (APR), corresponding sometimes to a nominal APR and sometimes to an effective APR (EAPR), is the interest rate for a whole year (annualized), rather than just a monthly fee/rate, as applied on a loan, mortgage loan, credit card, etc. It is a finance charge expressed as an annual rate. Those terms have formal, legal definitions in some countries or legal jurisdictions, but in the United States: :* The ''nominal APR'' is the simple-interest rate (for a year). :* The ''effective APR'' is the fee+compound interest rate (calculated across a year). "Subject: Regulation AA", Alfred F."Bob" Blair, Jr., US Federal Reserve, 2008-06-28, webpage: US-Federal-Reserve-R1314 In some areas, the ''annual percentage rate'' (APR) is the simplified counterpart to the effective interest rate that the borrower will pay on a loan. In many countries and jurisdictions, lenders (such as banks) are required to disclose the "cost" of borrowing in some standardiz ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Effective Interest Rate
The effective interest rate (EIR), effective annual interest rate, annual equivalent rate (AER) or simply effective rate is the percentage of interest on a loan or financial product if compound interest accumulates in periods different than a year. It is the compound interest payable annually in arrears, based on the nominal interest rate. It is used to compare the interest rates between loans with different compounding periods. In a situation where a 10% interest rate is compounded annually, its effective interest rate would also be 10%. Calculation The effective interest rate is calculated as if compounded annually. The effective rate is calculated in the following way, where ''r'' is the effective annual rate, ''i'' the nominal rate, and ''n'' the number of compounding periods per year (for example, 12 for monthly compounding): : r \ = \ \left(1+\frac\right)^n - 1 For example, a nominal interest rate of 6% compounded monthly is equivalent to an effective interest rate of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compound Interest
Compound interest is interest accumulated from a principal sum and previously accumulated interest. It is the result of reinvesting or retaining interest that would otherwise be paid out, or of the accumulation of debts from a borrower. Compound interest is contrasted with Interest#Calculation, simple interest, where previously accumulated interest is not added to the principal amount of the current period. Compounded interest depends on the simple interest rate applied and the frequency at which the interest is compounded. Compounding frequency The ''compounding frequency'' is the number of times per given unit of time the accumulated interest is capitalized, on a regular basis. The frequency could be yearly, half-yearly, quarterly, monthly, weekly, daily, continuous compounding, continuously, or not at all until maturity. For example, monthly capitalization with interest expressed as an annual rate means that the compounding frequency is 12, with time periods measured in m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compound Annual Growth Rate
Compound annual growth rate (CAGR) is a business, economics and investing term representing the mean annualized growth rate for compounding values over a given time period. CAGR smoothes the effect of volatility of periodic values that can render arithmetic means less meaningful. It is particularly useful to compare growth rates of various data values, such as revenue growth of companies, or of economic values, over time. Equation For annual values, CAGR is defined as: :\mathrm(t_0,t_n) = \left( \frac \right)^\frac - 1 where V(t_0) is the initial value, V(t_n) is the end value, and t_n - t_0 is the number of years. CAGR can also be used to calculate mean annualized growth rates on quarterly or monthly values. The numerator of the exponent would be the value of 4 in the case of quarterly, and 12 in the case of monthly, with the denominator being the number of corresponding periods involved. In practice, CAGR calculations are often performed in Microsoft Excel. A convenient ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exponential Growth
Exponential growth occurs when a quantity grows as an exponential function of time. The quantity grows at a rate directly proportional to its present size. For example, when it is 3 times as big as it is now, it will be growing 3 times as fast as it is now. In more technical language, its instantaneous rate of change (that is, the derivative) of a quantity with respect to an independent variable is proportional to the quantity itself. Often the independent variable is time. Described as a function, a quantity undergoing exponential growth is an exponential function of time, that is, the variable representing time is the exponent (in contrast to other types of growth, such as quadratic growth). Exponential growth is the inverse of logarithmic growth. Not all cases of growth at an always increasing rate are instances of exponential growth. For example the function f(x) = x^3 grows at an ever increasing rate, but is much slower than growing exponentially. For example, w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |