|
Free Logic
A free logic is a logic with fewer existential presuppositions than classical logic. Free logics may allow for terms that do not denote any object. Free logics may also allow models that have an empty domain. A free logic with the latter property is an inclusive logic. Explanation In classical logic there are theorems that clearly presuppose that there is something in the domain of discourse. Consider the following classically valid theorems. :1. \forall xA \Rightarrow \exists xA :2. \forall x \forall rA(x) \Rightarrow \forall rA(r) :3. \forall rA(r) \Rightarrow \exists xA(x) A valid scheme in the theory of equality which exhibits the same feature is :4. \forall x(Fx \rightarrow Gx) \land \exists xFx \rightarrow \exists x(Fx \land Gx) Informally, if F is '=y', G is 'is Pegasus', and we substitute 'Pegasus' for y, then (4) appears to allow us to infer from 'everything identical with Pegasus is Pegasus' that something is identical with Pegasus. The problem comes from s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logic
Logic is the study of correct reasoning. It includes both formal and informal logic. Formal logic is the study of deductively valid inferences or logical truths. It examines how conclusions follow from premises based on the structure of arguments alone, independent of their topic and content. Informal logic is associated with informal fallacies, critical thinking, and argumentation theory. Informal logic examines arguments expressed in natural language whereas formal logic uses formal language. When used as a countable noun, the term "a logic" refers to a specific logical formal system that articulates a proof system. Logic plays a central role in many fields, such as philosophy, mathematics, computer science, and linguistics. Logic studies arguments, which consist of a set of premises that leads to a conclusion. An example is the argument from the premises "it's Sunday" and "if it's Sunday then I don't have to work" leading to the conclusion "I don't have to wor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Karel Lambert
Karel Lambert (born 1928) is an American philosopher and logician at the University of California, Irvine and the University of Salzburg. He has written extensively on the subject of free logic, a term which he coined. Lambert's law Lambert's law is the major principle in any free definite description theory that says: For all x, x = the y (A) if and only if (A(x/y) & for all y (if A then y = x)). Free logic itself is an adjustment of a given standard predicate logic such as to relieve it of existential assumptions, and so make it a free logic. Taking Bertrand Russell's predicate logic in his ''Principia Mathematica'' as standard, one replaces universal instantiation, \forall x \,\phi x \rightarrow \phi y, with universal specification (\forall x \,\phi x \land E!y \,\phi y) \rightarrow \phi z. Thus universal statements, like "All men are mortal," or "Everything is a unicorn," do not presuppose that there are men or that there is anything. These would be symbolized, with the ap ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triangle Of Opposition
In the system of Aristotelian logic, the triangle of opposition is a diagram representing the different ways in which each of the three propositions of the system is logically related ('opposed') to each of the others. The system is also useful in the analysis of syllogistic logic, serving to identify the allowed logical conversions from one type to another. In the 19th and 20th centuries, other triangles were proposed, including Nicolai A. Vasiliev's triangle, the Jespersenian Triangle, Ginzberg’s triangle of contraries and Sir William Hamilton’s subcontraries. See also * Lambda cube * Logical cube * Logical hexagon * Square of opposition In term logic (a branch of philosophical logic), the square of opposition is a diagram representing the relations between the four basic categorical propositions. The origin of the square can be traced back to Aristotle's tractate '' On Int ... References External links [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Square Of Opposition
In term logic (a branch of philosophical logic), the square of opposition is a diagram representing the relations between the four basic categorical propositions. The origin of the square can be traced back to Aristotle's tractate '' On Interpretation'' and its distinction between two oppositions: contradiction and contrariety. However, Aristotle did not draw any diagram; this was done several centuries later by Boethius. Summary In traditional logic, a proposition (Latin: ''propositio'') is a spoken assertion (''oratio enunciativa''), not the meaning of an assertion, as in modern philosophy of language and logic. A ''categorical proposition'' is a simple proposition containing two terms, subject () and predicate (), in which the predicate is either asserted or denied of the subject. Every categorical proposition can be reduced to one of four logical forms, named , , , and based on the Latin ' (I affirm), for the affirmative propositions and , and ' (I deny), for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
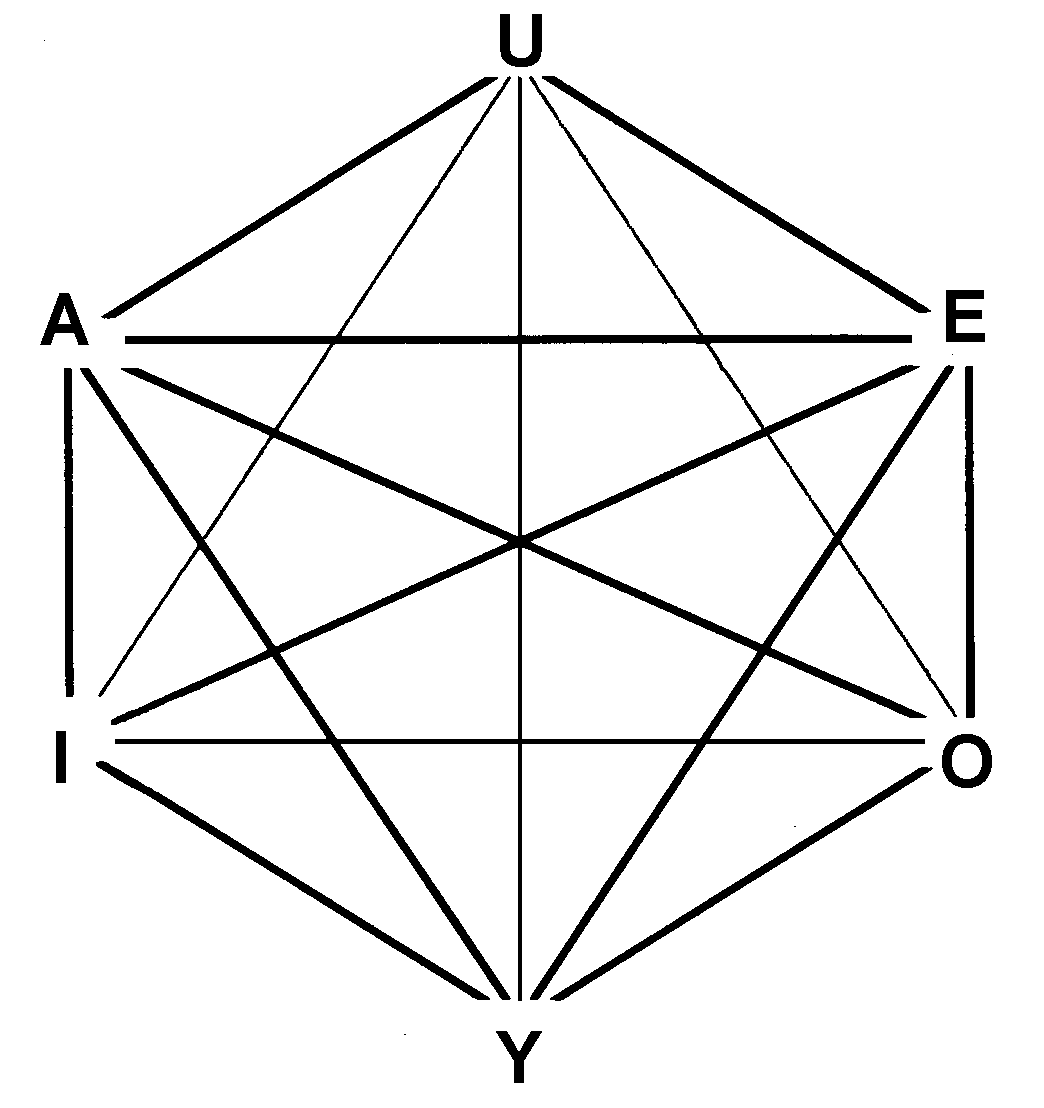
Logical Hexagon
In philosophical logic, the logical hexagon (also called the hexagon of opposition) is a conceptual model of the relationships between the truth values of six statements. It is an extension of Aristotle's square of opposition. It was discovered independently by both Augustin Sesmat and Robert Blanché. This extension consists in introducing two statements U and Y. Whereas U is the disjunction of A and E, Y is the conjunction of the two traditional particulars I and O. Summary of relationships The traditional square of opposition demonstrates two sets of contradictories A and O, and E and I (i.e. they cannot both be true and cannot both be false), two contraries A and E (i.e. they can both be false, but cannot both be true), and two subcontraries I and O (i.e. they can both be true, but cannot both be false) according to Aristotle’s definitions. However, the logical hexagon provides that U and Y are also contradictory. Interpretations The logical hexagon may be interpr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logical Cube
In the system of Term logic, Aristotelian logic, the logical cube is a Diagram, diagram representing the different ways in which each of the eight propositions of the Formal system, system is logically related ('opposed') to each of the others. The system is also useful in the analysis of Term logic, syllogistic logic, serving to identify the allowed logical conversions from one type to another.Paul Dekker, 2015, "Not Only Barbara", Journal of Logic, Language and Information 24(2), pp. 95-129. See also *Lambda cube *Logical hexagon *Square of opposition *Triangle of opposition References Conceptual models Term logic {{logic-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wesley C
Wesley may refer to: People and fictional characters * Wesley (name), a given name and a surname Places United States * Wesley, Arkansas, an unincorporated community * Wesley, Georgia, an unincorporated community * Wesley Township, Will County, Illinois * Wesley, Iowa, a city in Kossuth County * Wesley Township, Kossuth County, Iowa * Wesley, Maine, a town * Wesley Township, Washington County, Ohio * Wesley, Oklahoma, an unincorporated community * Wesley, Indiana, an unincorporated town * Wesley, West Virginia, an unincorporated community Elsewhere * Wesley, a hamlet in the township of Stone Mills, Ontario, Canada * Wesley, Dominica, a village * Wesley, New Zealand, a suburb of Auckland * Wesley, Eastern Cape, South Africa, a town Schools * Wesley College (other) * Wesley Institute, Sydney, Australia * Wesley Seminary, Marion, Indiana * Wesley Biblical Seminary, Jackson, Mississippi * Wesley Theological Seminary, Washington, DC * Wesley University of Science and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Theory Of Descriptions
The theory of descriptions is the philosopher Bertrand Russell's most significant contribution to the philosophy of language. It is also known as Russell's theory of descriptions (commonly abbreviated as RTD). In short, Russell argued that the syntactic form of descriptions (phrases that took the form of "The flytrap" and "A flytrap") is misleading, as it does not correlate their logical and/or semantic architecture. While descriptions may seem like fairly uncontroversial phrases, Russell argued that providing a satisfactory analysis of the linguistic and logical properties of a description is vital to clarity in important philosophical debates, particularly in semantic arguments, epistemology and metaphysical elements. Since the first development of the theory in Russell's 1905 paper "On Denoting", RTD has been hugely influential and well-received within the philosophy of language. However, it has not been without its critics. In particular, the philosophers P. F. Strawson and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bertrand Russell
Bertrand Arthur William Russell, 3rd Earl Russell, (18 May 1872 – 2 February 1970) was a British philosopher, logician, mathematician, and public intellectual. He had influence on mathematics, logic, set theory, and various areas of analytic philosophy.Stanford Encyclopedia of Philosophy"Bertrand Russell", 1 May 2003. He was one of the early 20th century's prominent logicians and a founder of analytic philosophy, along with his predecessor Gottlob Frege, his friend and colleague G. E. Moore, and his student and protégé Ludwig Wittgenstein. Russell with Moore led the British "revolt against British idealism, idealism". Together with his former teacher Alfred North Whitehead, A. N. Whitehead, Russell wrote ''Principia Mathematica'', a milestone in the development of classical logic and a major attempt to reduce the whole of mathematics to logic (see logicism). Russell's article "On Denoting" has been considered a "paradigm of philosophy". Russell was a Pacifism, pacifist who ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Willard Van Orman Quine
Willard Van Orman Quine ( ; known to his friends as "Van"; June 25, 1908 – December 25, 2000) was an American philosopher and logician in the analytic tradition, recognized as "one of the most influential philosophers of the twentieth century". He was the Edgar Pierce Chair of Philosophy at Harvard University from 1956 to 1978. Quine was a teacher of logic and set theory. He was famous for his position that first-order logic is the only kind worthy of the name, and developed his own system of mathematics and set theory, known as New Foundations. In the philosophy of mathematics, he and his Harvard colleague Hilary Putnam developed the Quine–Putnam indispensability argument, an argument for the Philosophy of mathematics#Empiricism, reality of mathematical entities.Colyvan, Mark"Indispensability Arguments in the Philosophy of Mathematics" The Stanford Encyclopedia of Philosophy (Fall 2004 Edition), Edward N. Zalta (ed.). He was the main proponent of the view that philosophy is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jaakko Hintikka
Kaarlo Jaakko Juhani Hintikka (; ; 12 January 1929 – 12 August 2015) was a Finnish philosopher and logician. Hintikka is regarded as the founder of formal epistemic logic and of game semantics for logic. Life and career Hintikka was born in Helsingin maalaiskunta (now Vantaa). In 1953, he received his doctorate from the University of Helsinki for a thesis entitled ''Distributive Normal Forms in the Calculus of Predicates''. He was a student of Georg Henrik von Wright. Hintikka was a Junior Fellow at Harvard University (1956-1969), and held several professorial appointments at the University of Helsinki, the Academy of Finland, Stanford University, Florida State University and finally Boston University from 1990 until his death. He was the prolific author or co-author of over 30 books and over 300 scholarly articles, Hintikka contributed to mathematical logic, philosophical logic, the philosophy of mathematics, epistemology, language theory, and the philosophy of scienc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Existential Clause
An existential clause is a clause (grammar), clause that refers to the existence or presence of something, such as "There is a God" and "There are boys in the yard". The use of such clauses can be considered analogous to existential quantification in predicate logic, which is often expressed with the phrase "There exist(s)...". Different languages have different ways of forming and using existential clauses. For details on the English language, English forms, see English grammar#"There", English grammar: ''There'' as pronoun. Formation Many languages form existential clauses without any particular marker by simply using forms of the normal copula (linguistics), copula verb (the equivalent of English ''be''), the subject (grammar), subject being the noun (phrase) referring to the thing whose existence is asserted. For example, the Finnish language, Finnish sentence , meaning "There are boys in the yard", is literally "On the yard is boys". Some languages have a different verb f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |