|
Frames Of Reference
In physics and astronomy, a frame of reference (or reference frame) is an abstract coordinate system, whose origin, orientation, and scale have been specified in physical space. It is based on a set of reference points, defined as geometric points whose position is identified both mathematically (with numerical coordinate values) and physically (signaled by conventional markers). An important special case is that of '' inertial reference frames'', a stationary or uniformly moving frame. For ''n'' dimensions, reference points are sufficient to fully define a reference frame. Using rectangular Cartesian coordinates, a reference frame may be defined with a reference point at the origin and a reference point at one unit distance along each of the ''n'' coordinate axes. In Einsteinian relativity, reference frames are used to specify the relationship between a moving observer and the phenomenon under observation. In this context, the term often becomes observational frame o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Physics
Physics is the scientific study of matter, its Elementary particle, fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge which relates to the order of nature, or, in other words, to the regular succession of events." It is one of the most fundamental scientific disciplines. "Physics is one of the most fundamental of the sciences. Scientists of all disciplines use the ideas of physics, including chemists who study the structure of molecules, paleontologists who try to reconstruct how dinosaurs walked, and climatologists who study how human activities affect the atmosphere and oceans. Physics is also the foundation of all engineering and technology. No engineer could design a flat-screen TV, an interplanetary spacecraft, or even a better mousetrap without first understanding the basic laws of physics. (...) You will come to see physics as a towering achievement of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Galilean Frame Of Reference
In classical physics and special relativity, an inertial frame of reference (also called an inertial space or a Galilean reference frame) is a frame of reference in which objects exhibit inertia: they remain at rest or in uniform motion relative to the frame until acted upon by external forces. In such a frame, the laws of nature can be observed without the need to correct for acceleration. All frames of reference with zero acceleration are in a state of constant rectilinear motion (straight-line motion) with respect to one another. In such a frame, an object with zero net force acting on it, is perceived to move with a constant velocity, or, equivalently, Newton's first law of motion holds. Such frames are known as inertial. Some physicists, like Isaac Newton, originally thought that one of these frames was absolute — the one approximated by the fixed stars. However, this is not required for the definition, and it is now known that those stars are in fact moving, relative ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Configuration Space (physics)
In classical mechanics, the parameters that define the configuration of a system are called '' generalized coordinates,'' and the space defined by these coordinates is called the configuration space of the physical system. It is often the case that these parameters satisfy mathematical constraints, such that the set of actual configurations of the system is a manifold in the space of generalized coordinates. This manifold is called the configuration manifold of the system. Notice that this is a notion of "unrestricted" configuration space, i.e. in which different point particles may occupy the same position. In mathematics, in particular in topology, a notion of "restricted" configuration space is mostly used, in which the diagonals, representing "colliding" particles, are removed. Examples A particle in 3D space The position of a single particle moving in ordinary Euclidean 3-space is defined by the vector q=(x,y,z), and therefore its ''configuration space'' is Q=\mathbb^3. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Manifold
In mathematics, a manifold is a topological space that locally resembles Euclidean space near each point. More precisely, an n-dimensional manifold, or ''n-manifold'' for short, is a topological space with the property that each point has a Neighbourhood (mathematics), neighborhood that is homeomorphic to an open (topology), open subset of n-dimensional Euclidean space. One-dimensional manifolds include Line (geometry), lines and circles, but not Lemniscate, self-crossing curves such as a figure 8. Two-dimensional manifolds are also called Surface (topology), surfaces. Examples include the Plane (geometry), plane, the sphere, and the torus, and also the Klein bottle and real projective plane. The concept of a manifold is central to many parts of geometry and modern mathematical physics because it allows complicated structures to be described in terms of well-understood topological properties of simpler spaces. Manifolds naturally arise as solution sets of systems of equations ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Algebra
Algebra is a branch of mathematics that deals with abstract systems, known as algebraic structures, and the manipulation of expressions within those systems. It is a generalization of arithmetic that introduces variables and algebraic operations other than the standard arithmetic operations, such as addition and multiplication. Elementary algebra is the main form of algebra taught in schools. It examines mathematical statements using variables for unspecified values and seeks to determine for which values the statements are true. To do so, it uses different methods of transforming equations to isolate variables. Linear algebra is a closely related field that investigates linear equations and combinations of them called '' systems of linear equations''. It provides methods to find the values that solve all equations in the system at the same time, and to study the set of these solutions. Abstract algebra studies algebraic structures, which consist of a set of mathemati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Geometry
Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician who works in the field of geometry is called a ''List of geometers, geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point (geometry), point, line (geometry), line, plane (geometry), plane, distance, angle, surface (mathematics), surface, and curve, as fundamental concepts. Originally developed to model the physical world, geometry has applications in almost all sciences, and also in art, architecture, and other activities that are related to graphics. Geometry also has applications in areas of mathematics that are apparently unrelated. For example, methods of algebraic geometry are fundamental in Wiles's proof of Fermat's Last Theorem, Wiles's proof of Fermat's ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
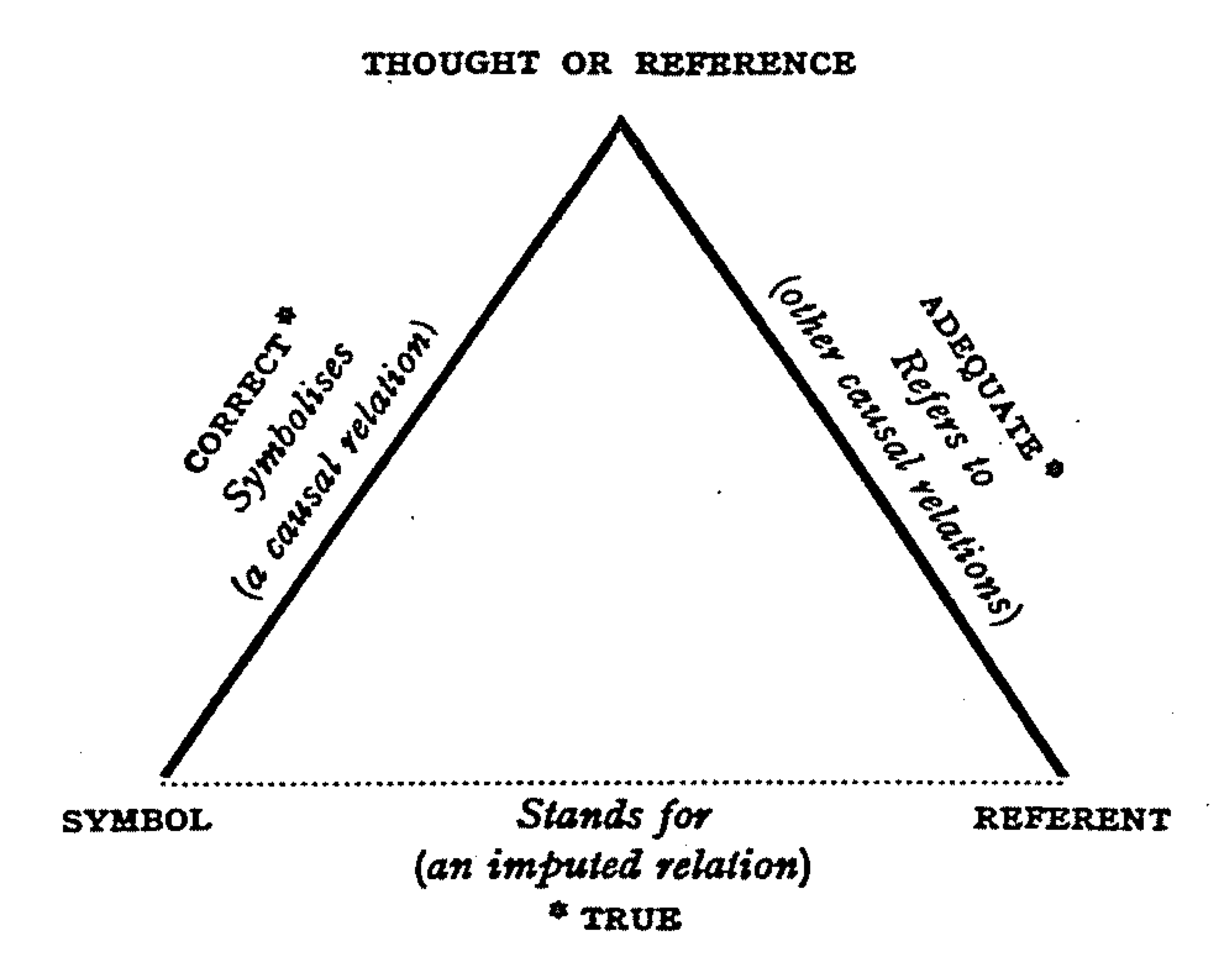 |
Reference Frame And Observer
A reference is a relationship between objects in which one object designates, or acts as a means by which to connect to or link to, another object. The first object in this relation is said to ''refer to'' the second object. It is called a ''name'' for the second object. The next object, the one to which the first object refers, is called the '' referent'' of the first object. A name is usually a phrase or expression, or some other symbolic representation. Its referent may be anything – a material object, a person, an event, an activity, or an abstract concept. References can take on many forms, including: a thought, a sensory perception that is audible ( onomatopoeia), visual (text), olfactory, or tactile, emotional state, relationship with other, spacetime coordinates, symbolic or alpha-numeric, a physical object, or an energy projection. In some cases, methods are used that intentionally hide the reference from some observers, as in cryptography. References feature i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Lie Group
In mathematics, a Lie group (pronounced ) is a group (mathematics), group that is also a differentiable manifold, such that group multiplication and taking inverses are both differentiable. A manifold is a space that locally resembles Euclidean space, whereas groups define the abstract concept of a binary operation along with the additional properties it must have to be thought of as a "transformation" in the abstract sense, for instance multiplication and the taking of inverses (to allow division), or equivalently, the concept of addition and subtraction. Combining these two ideas, one obtains a continuous group where multiplying points and their inverses is continuous. If the multiplication and taking of inverses are smoothness, smooth (differentiable) as well, one obtains a Lie group. Lie groups provide a natural model for the concept of continuous symmetry, a celebrated example of which is the circle group. Rotating a circle is an example of a continuous symmetry. For an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Non-inertial Frame Of Reference
A non-inertial reference frame (also known as an accelerated reference frame) is a frame of reference that undergoes acceleration with respect to an Inertial frame of reference, inertial frame. An accelerometer at rest in a non-inertial frame will, in general, detect a non-zero acceleration. While the laws of motion are the same in all inertial frames, in non-inertial frames, they vary from frame to frame, depending on the acceleration. In classical mechanics it is often possible to explain the motion of bodies in non-inertial reference frames by introducing additional fictitious forces (also called inertial forces, Pseudo-force, pseudo-forces, and D'Alembert's principle, d'Alembert forces) to Newton's laws of motion, Newton's second law. Common examples of this include the Coriolis force and the centrifugal force (fictitious), centrifugal force. In general, the expression for any fictitious force can be derived from the acceleration of the non-inertial frame. As stated by Goodman ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Inertial Frame
In classical physics and special relativity, an inertial frame of reference (also called an inertial space or a Galilean reference frame) is a frame of reference in which objects exhibit inertia: they remain at rest or in uniform motion relative to the frame until acted upon by external forces. In such a frame, the laws of nature can be observed without the need to correct for acceleration. All frames of reference with zero acceleration are in a state of constant rectilinear motion (straight-line motion) with respect to one another. In such a frame, an object with zero net force acting on it, is perceived to move with a constant velocity, or, equivalently, Newton's first law of motion holds. Such frames are known as inertial. Some physicists, like Isaac Newton, originally thought that one of these frames was absolute — the one approximated by the fixed stars. However, this is not required for the definition, and it is now known that those stars are in fact moving, relative ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Eigenvectors
In linear algebra, an eigenvector ( ) or characteristic vector is a Vector (mathematics and physics), vector that has its direction (geometry), direction unchanged (or reversed) by a given linear map, linear transformation. More precisely, an eigenvector \mathbf v of a linear transformation T is scalar multiplication, scaled by a constant factor \lambda when the linear transformation is applied to it: T\mathbf v=\lambda \mathbf v. The corresponding eigenvalue, characteristic value, or characteristic root is the multiplying factor \lambda (possibly a negative number, negative or complex number, complex number). Euclidean vector, Geometrically, vectors are multi-dimensional quantities with magnitude and direction, often pictured as arrows. A linear transformation Rotation (mathematics), rotates, Scaling (geometry), stretches, or Shear mapping, shears the vectors upon which it acts. A linear transformation's eigenvectors are those vectors that are only stretched or shrunk, with nei ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
 |
Normal Modes
A normal mode of a dynamical system is a pattern of motion in which all parts of the system move sinusoidally with the same frequency and with a fixed phase relation. The free motion described by the normal modes takes place at fixed frequencies. These fixed frequencies of the normal modes of a system are known as its natural frequencies or resonant frequencies. A physical object, such as a building, bridge, or molecule, has a set of normal modes and their natural frequencies that depend on its structure, materials and boundary conditions. The most general motion of a linear system is a superposition of its normal modes. The modes are normal in the sense that they can move independently, that is to say that an excitation of one mode will never cause motion of a different mode. In mathematical terms, normal modes are orthogonal to each other. General definitions Mode In the wave theory of physics and engineering, a mode in a dynamical system is a standing wave stat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |